Difference between revisions of "Signal Representation/The Fourier Transform and its Inverse"
| (92 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Aperiodic Signals - Impulses |
| − | |Vorherige Seite= | + | |Vorherige Seite=Fourier Series |
| − | |Nächste Seite= | + | |Nächste Seite=Special Cases of Impulse Signals |
}} | }} | ||
| − | + | == # OVERVIEW OF THE THIRD MAIN CHAPTER # == | |
| + | <br> | ||
| + | In the second chapter periodic signals were described by different harmonic oscillations (»Fourier series«). | ||
| + | If one reduces – at least mentally – the repetition frequency of a periodic signal more and more, i.e., the period duration becomes longer and longer, then one comes from the periodic signal to the unique »aperiodic signal« – often also called »pulse«. | ||
| + | In the following, such aperiodic and pulse–shaped signals are considered and mathematically described in the time and frequency domain. | ||
| − | + | The chapter contains in detail: | |
| + | # The derivation of the two »Fourier integrals« from the Fourier series, | ||
| + | # the extension of the Fourier integral to the »Fourier transform« by means of distributions, | ||
| + | # »some special cases« of pulses: »rectangular pulse« and »Gaussian pulse«, | ||
| + | # the »laws of Fourier transform«, and finally | ||
| + | # the meaning of the »convolution operation« and its various applications. | ||
| − | |||
| − | + | »Laplace transform« and »Hilbert transform«, which are only applicable to causal signals or systems, will be treated in the second book »Linear Time-invariant Systems«. | |
| − | |||
| − | |||
| − | |||
| − | + | ==Properties of aperiodic signals== | |
| − | + | <br> | |
| − | + | In the last chapter periodic signals were considered. The essential characteristic of these signals is, that you can specify a period duration $T_0$ for them. If such a period duration cannot be indicated or – which is the same in practice – has an infinitely large value $T_0$, one speaks of an »aperiodic signal«. | |
| − | |||
| + | For the present chapter »Aperiodic Signals – Pulses» the following conditions should apply: | ||
| + | #The considered signals $x(t)$ are aperiodic and "energy-limited": They possess a finite energy $E_x$ and a negligible $($medium$)$ power $P_x$. | ||
| + | #Often the energy of these signals is concentrated on a relatively short time range, so that one also speaks of »pulse-like signals« or »pulses«. | ||
| − | |||
| − | |||
| − | |||
| − | {{ | + | {{GraueBox|TEXT= |
| + | [[File:P_ID550__Sig_T_3_1_S1.png|right|frame|Energy-limited signal $x_1(t)$ and <br>power-limited signal $x_2(t)$]] | ||
| + | $\text{Example 1:}$ | ||
| + | The figure shows a rectangular pulse $x_1(t)$ with amplitude $A$ and duration $T$ as an example of an aperiodic and time-limited signal. This pulse has | ||
| + | #the finite signal energy ⇒ here: $E_1=A^2 \cdot T$, and | ||
| + | #the power $P_1=0$. | ||
| − | |||
| − | |||
| − | $ | + | A power-limited signal, for example the cosine signal $x_2(t)$ shown below, has |
| + | #always a finite power ⇒ here: $P_2=A^2/2$, and | ||
| + | #thus also an infinitely large signal energy: $E_2 \to \infty$.}} | ||
| − | + | ||
| + | ==Closer examination of the Fourier coefficients== | ||
| + | <br> | ||
| + | We assume a periodic signal $x_{\rm P}(t)$ with period duration $T_0$ which corresponds to the explanations in section [[Signal_Representation/Fourier_Series#Complex_Fourier_series|»Complex Fourier series«]]. | ||
| + | [[File:P_ID538__Sig_T_3_1_S2b_rah.png|right|frame|Periodic signal $x_{\rm P}(t)$ and $x_{\rm P}\hspace{0.01cm}'(t)$ and its line spectra]] | ||
| + | *This signal can be described as follows: | ||
| + | :$$x_{\rm P}(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j 2 \pi \hspace{0.01cm}{\it n} \hspace{0.01cm}\it t / T_{\rm 0}}.$$ | ||
| + | |||
| + | *The Fourier coefficients are generally complex $($with $D_{-n}=D_n^\ast)$: | ||
| − | $$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{ | + | :$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{0.01cm}{\it n} \it t / T_{\rm 0}}\, {\rm d}t.$$ |
| − | + | *The corresponding spectral function $X_{\rm P}(f)$ is a »line spectrum« with spectral lines in the distance $f_0=1/T_0$: | |
| − | $$X_{\rm P}(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$ | + | :$$X_{\rm P}(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$ |
| − | + | *The upper figure shows on the left the periodic time signal $x_{\rm P}(t)$ and on the right the corresponding magnitude spectrum $|X_{\rm P}(f)|$. This is merely a schematic sketch. | |
| + | |||
| + | *If $x_{\rm P}(t)$ is a real and even function, then $X_{\rm P}(f)$ is also real and even. The equation $X_{\rm P}(f) = |X_{\rm P}(f)|$ is only valid if all spectral lines are positive. | ||
| + | <br clear=all> | ||
| + | In the lower figure on the left side another periodic signal ${x_{\rm P}}\hspace{0.01cm}'(t)$ with double period duration ${T_0}\hspace{0.01cm}' = 2 \cdot T_0$ is displayed. The following applies to this signal: | ||
| + | |||
| + | :$${x_{\rm P}}'(t)=\sum^{+\infty}_{n=-\infty}{\it D_n}'\cdot {\rm e}^{{\rm j} 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}\hspace{0.01cm}'} \hspace{0.3cm}{\rm with}\hspace{0.3cm}{\it D_n}'=\frac{1}{{T_0}\hspace{0.01cm}'}\cdot \int^{{+T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}\hspace{0.01cm}'}\, {\rm d}\it t.$$ | ||
| − | + | In the range from $-T_0/2$ to $+T_0/2$ the two signals $x_{\rm P}(t)$ and $x_{\rm P}\hspace{0.01cm}'(t)$ are identical. | |
| − | + | We will also consider the spectral function ${X_{\rm P} }'(f)$ according to the right sketch: | |
| + | *Due to the double period duration $({T_0}' = 2 \cdot T_0)$ the spectral lines are now closer together $({f_0}' = f_0/2)$. | ||
| − | + | *Both red marked coefficients $D_n$ und ${D_{2n}}'$ belong to the same physical frequency $f = n \cdot f_0 = 2n \cdot {f_0}'$. | |
| − | |||
| − | $${ | ||
| − | |||
| − | + | We recognize by a comparison of the two coefficients | |
| − | + | ||
| − | + | :$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} \it t / T_{\rm 0}}\, {\rm d}t \hspace{0.5cm}\text{and} \hspace{0.5cm} {D_{2n}}'=\frac{1}{{T_0}'}\cdot \int^{+{T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 4 \pi \hspace{-0.05cm}{\it n} \it t / {T_{\rm 0}}'}\, {\rm d}t \text{:} $$ | |
| + | #${x_{\rm P}}'(t) \equiv 0$ between $T_0/2$ and ${T_0}'/2$ and also in a symmetrical interval for negative times. | ||
| + | #Therefore the integration limits can be restricted to $\pm T_0/2$. | ||
| + | #Inside the new integration limits: ${x_{\rm P}}'(t)$ can be replaced by $x_{\rm P}(t)$. | ||
| + | #If we set ${T_0}' = 2T_0$ in the above equation, we get: | ||
| + | |||
| + | :$${D_{2n}}'=\frac{1}{2T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} t / T_{\rm 0}}\, {\rm d}t = {D_n}/{2} .$$ | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{We summarize this result briefly:}$ | ||
| + | *The spectral line of the signal ${x_{\rm P} }'(t)$ at frequency $f = n \cdot {f_0}'$ is denoted by ${D_{2n} }'$ $($see lower graph on the right$)$. | ||
| − | $$ | + | *This line has exactly half the size of the spectral line $D_n$ of the signal $x_{\rm P}(t)$ at the same physical frequency $f$ $($see upper graph on the right$)$. |
| − | * | + | *The spectral function ${X_{\rm P} }'(f)$ has opposite $X_{\rm P}(f)$ additional spectral lines at $(n + 1/2) \cdot f_0$ $($see lower graph on the left$)$. |
| − | |||
| − | |||
| − | + | *These additional lines lead to the fact that in the time domain every second pulse of $x_{\rm P}(t)$ – located by $n \cdot T_0$ $(n$ odd$)$ – is cancelled.}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==From the periodic to the aperiodic signal== | ||
| + | <br> | ||
| + | We now take up the considerations in the previous section and select the period duration ${T_0}'$ of ${x_{\rm P}}'(t)$ generally by an integer factor $k$ greater than the period duration $T_0$ of ${x_{\rm P}}(t)$. Then the previous statements can be generalized: | ||
| − | + | [[File:P_ID398__Sig_T_3_1_S3_rah.png|right|frame|From the periodic to the aperiodic signal]] | |
| − | + | *The line spacing is smaller for ${X_{\rm P}}'(f)$ by the factor $k$ than for the spectrum ${X_{\rm P}}(f)$. | |
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | + | *To emphasize this fact, we denote the discrete frequency variable of function ${X_{\rm P}}'(f)$ with $\nu$ instead of $n$. The following applies: | |
| + | :$$\nu=k \cdot n.$$ | ||
| + | *It applies for the red marked spectral line of signal ${x_{\rm P}}'(t)$ at frequency $f=n \cdot f_0 =\nu \cdot {f_0}'$: | ||
| + | :$${D_\nu}' = {1}/{k} \cdot D_n.$$ | ||
| − | + | *If one now chooses – as shown schematically in the graph – the factor $k$ and thus the period duration ${T_0}'$ always larger and finally lets it go to infinity, then | |
| − | + | # the periodic signal ${x_{\rm P}}(t)$ changes to the aperiodic signal $x(t)$, | |
| − | + | #the line spectrum ${X_{\rm P}}(f)$ can be replaced by the continuous spectrum $X(f)$. | |
| + | <br clear=all> | ||
| + | ==The first Fourier integral== | ||
| + | <br> | ||
| + | Concerning the spectral functions $X_{\rm P}(f)$ and $X(f)$ the following statements can be made: | ||
| + | *The individual spectral lines now lie as close together as desired $({f_0}'=1/{T_0}' \to 0)$. | ||
| + | *In the spectral function $X(f)$ all possible $($not only discrete$)$ frequencies now occur within certain intervals ⇒ $X(f)$ is no longer a line spectrum. | ||
| − | + | *The contribution of each individual frequency $f$ to the signal $x(t)$ is negligibly small $(k \to \infty,\ {D_{\nu}}' \to 0)$. | |
| + | |||
| + | *Because of the infinite number of frequencies there is a finite result in total. | ||
| − | + | *Instead of calculating the Fourier coefficients ${D_{\nu}}'$: Now a spectral density $X(f)$ is calculated. For the frequency $f=\nu\cdot {f_0}'$ then applies: | |
| − | |||
| − | * | ||
| − | |||
| − | |||
: $$X(f = {\rm \nu} {f_{\rm 0}}') = \lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm} 0} ({{D_{\rm \nu}}'}/{{f_{\rm 0}}'}) = \lim_{{T_{\rm 0}}' \to \infty} ({D_{\rm \nu}}' \cdot {T_{\rm 0}}').$$ | : $$X(f = {\rm \nu} {f_{\rm 0}}') = \lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm} 0} ({{D_{\rm \nu}}'}/{{f_{\rm 0}}'}) = \lim_{{T_{\rm 0}}' \to \infty} ({D_{\rm \nu}}' \cdot {T_{\rm 0}}').$$ | ||
| − | * | + | *The spectral function $X(f)$ of the aperiodic signal $x(t)$ is visible in the spectrum $X_{\rm P}(f)$ of the periodic signal $x_{\rm P}(t)$ as envelope $($see graphics in the last section$)$. |
| − | |||
| − | + | *In the lower graphic ${D_{\nu}}'$ corresponds to the red-shaded area of the frequency interval around $\nu \cdot {f_0}'$ with width ${f_0}'$. | |
| − | + | If you use the equations given in the last section, you get | |
| − | $$X(f = {\rm \nu} \cdot {f_{\rm 0}}') = \lim_{{T_{\rm 0}'} \to \infty} \int ^{{T_{\rm 0}}'/2} _{-{T_{\rm 0}}'/2} x_{\rm P}(t) \, \cdot \, { \rm e}^{-\rm j 2\pi\nu \it {f_{\rm 0}}' t} \,{\rm d}t.$$ | + | :$$X(f = {\rm \nu} \cdot {f_{\rm 0}}') = \lim_{{T_{\rm 0}'} \to \infty} \int ^{{T_{\rm 0}}'/2} _{-{T_{\rm 0}}'/2} x_{\rm P}(t) \, \cdot \, { \rm e}^{-\rm j 2\pi\nu \it {f_{\rm 0}}' t} \,{\rm d}t.$$ |
| − | + | Through the common limit crossing $({T_0}' \to \infty, \ {f_0}' \to 0)$ the following transformations will happen: | |
| − | + | #From the periodic signal $x_{\rm P}(t)$ to the aperiodic signal $x(t)$. | |
| − | + | #From the discrete frequency $\nu \cdot {f_0}'$ to the continuous frequency variable $f$. | |
| − | + | Thus, a fundamental definition is obtained, which allows the calculation of the spectral function of an aperiodic time function. The name of this spectral transformation goes back to the French physicist [https://en.wikipedia.org/wiki/Joseph_Fourier »$\text{Jean-Baptiste Joseph Fourier}$«]. | |
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{First Fourier Integral:}$ | |
| − | $$ | + | The »'''spectral function'''« $($or short: the »'''spectrum'''«$)$ of an aperiodic and simultaneously energy limited signal $x(t)$ is to be calculated as follows |
| − | {{ | + | :$$X(f)= \hspace{0.05cm}\int_{-\infty} ^{ {+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$}} |
| − | + | The following $($German language$)$ learning video should clarify the statements of the last sections:<br> [[Kontinuierliche_und_diskrete_Spektren_(Lernvideo)|»Kontinuierliche und diskrete Spektren«]] ⇒ "Continuous and discrete spectra". | |
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 2:}$ | ||
| + | Given is the sketched time course $x(t)$. The corresponding spectrum $X(f)$ is searched for using the first Fourier integral: | ||
| + | [[File:P_ID330__Sig_T_3_1_S5_neu.png|right|frame|Rectangular pulse $x(t)$]] | ||
| + | *From the above representation we can see, that for $\vert t \vert > T/2$ the signal is $x(t) = 0$. | ||
| + | *This means that the integration interval can be limited to the range $\pm T/2$. | ||
| + | |||
| + | *This results in the approach: | ||
| + | |||
| + | :$$ \begin{align*} X(f) & = A \cdot \int_{- T/2}^{+T/2} {\rm e}^{- {\rm j2\pi} ft}\,{\rm d}t = \frac{ A}{- \rm j2\pi f}\left[ {\rm e}^{- {\rm j}2\pi ft}\right]_{-T/2}^{+T/2} \\ & = \frac{\it A} {- \rm j 2\pi f}\cdot \big[\cos({\rm \pi} f T) - {\rm j} \cdot \sin({\rm \pi} fT) - \cos({\rm \pi} fT) - {\rm j} \cdot \sin({\rm \pi} fT)\big] \end{align*}$$ | ||
| + | :$$\Rightarrow \hspace{0.5cm}X(f)=A\cdot \frac{\sin({\rm \pi} fT)}{ {\rm \pi} f},$$ | ||
| − | == | + | *If you extend numerator and denominator with $T$, you get: |
| + | |||
| + | :$$X(f)=A\cdot T \cdot\frac{\sin(\pi fT)}{\pi fT} = A\cdot T \cdot{\rm si }(\pi fT) = A\cdot T \cdot{\rm sinc }(fT).$$}} | ||
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definitions:}$ For abbreviation we define the following functions: | ||
| + | *»'''sinc–function«''' $($predominantly used in Anglo-American literature$)$ | ||
| + | :$${\rm sinc}( x ) = {\sin (\pi x) }/(\pi x ),$$ | ||
| − | + | *»'''si–function'''« or »$\text{splitting function}$« $($predominantly used in German literature$)$ | |
| − | + | :$${\rm si}\left( x \right) = \sin \left( x \right)/x = {\rm sinc}(x/\pi ).$$}} | |
| − | $$ | ||
| − | |||
| + | <u>Note:</u> In our $\rm LNTwww$ we mostly use the function ${\rm si}(x)$, but important results are also given in the ${\rm sinc}(x)$ form. | ||
| − | |||
| − | + | ==Fourier transform== | |
| + | <br> | ||
| + | The spectrum $X(f)$ of a signal $x(t)$ is according to the »first Fourier integral«: | ||
| − | $$X(f)= | + | :$$X(f)= \hspace{0.05cm}\int _{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$ |
| − | |||
| − | |||
| − | |||
| − | + | As shown in the last section with a simple example, this integral can be solved easily for an energy-limited signal $x(t)$. For non-energy limited signals, for example | |
| − | + | *a [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal|»DC signal«]], or | |
| − | |||
| − | |||
| − | |||
| − | * | ||
| + | *a [[ Signal_Representation/Harmonic_Oscillation|»harmonic oscillation«]], | ||
| − | + | we observe a divergence of the Fourier integral. Including a bilateral declining auxiliary function $\varepsilon (t)$, however, convergence can be forced: | |
| − | |||
| − | |||
| − | $$X(f)= \ | + | :$$X(f) = \lim_{\varepsilon \to 0} \int _{-\infty} ^{{+}\infty} x(t) \cdot {\rm e}^{\it -\varepsilon | \hspace{0.01cm} t \hspace{0.01cm} |} \cdot {\rm e}^{{-\rm j 2 \pi}\it ft} \,{\rm d}t.$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Such non-energy limited signals lead to so-called »Dirac delta functions« in the spectral domain, sometimes also called »distributions«. | |
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ | ||
| + | The generally valid functional relation $X(f) = F\big [x(t) \big ]$ is called »'''Fourier Transform'''«. For the short notation we use $($with the "white dot" for the time domain and the "filled dot" for the spectral domain$)$: | ||
| − | $$X(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,x(t).$$ | + | :$$X(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x(t).$$ |
| − | + | With a increasing signal, however, convergence is only achieved as long as the time function increases less than exponentially. }} | |
| − | {{ | + | {{GraueBox|TEXT= |
| − | + | [[File:P_ID655__Sig_T_3_1_S6.png|right|frame| Jump function and associated spectrum]] | |
| + | |||
| + | $\text{Example 3:}$ | ||
| + | We consider an acausal jump function | ||
| + | :$$x (t) = \left\{ {\begin{array}{*{20}c} { +1 } & { {\rm{for} }\quad t > 0,} \\ {-1 } & { {\rm{for} }\quad t < 0.} \\\end{array} } \right.$$ | ||
| + | This signal is shown in blue color in the left sketch. | ||
| − | + | Since the signal $x(t)$ extends to infinity on both sides, we must add a suitable convergence factor $\text{e}^{-\varepsilon \hspace{0.05cm} \cdot \hspace{0.05cm}\vert \hspace{0.05cm} t \hspace{0.05cm} \vert}$ with $($ $\varepsilon > 0)$ in order to calculate the Fourier transform for both sections. The resulting time function is then | |
| − | |||
| − | |||
| − | $$x_\varepsilon (t) = \left\{ {\begin{array}{*{20}c} {{\rm{e}}^{ - \varepsilon t} } & {{\rm{ | + | :$$x_\varepsilon (t) = \left\{ {\begin{array}{*{20}c} { {\rm{e} }^{ - \varepsilon \hspace{0.05cm} \cdot \hspace{0.05cm}t} } & { {\rm{for} }\quad t > 0,} \\ { {\rm{ - e} }^{\hspace{0.05cm}\varepsilon\hspace{0.05cm} \cdot \hspace{0.05cm} t} } & { {\rm{for} }\quad t < 0.} \\\end{array} } \right.$$ |
| − | + | Following a similar procedure as in section [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal#Dirac_.28delta.29_function_in_frequency_domain|»Dirac delta function in the frequency domain«]] results for the corresponding spectral function: | |
| − | $$X_\varepsilon (f) = \frac{1}{{\varepsilon + {\rm{j}}2{\rm{\pi }}f}} - \frac{1}{{\varepsilon - {\rm{j}}2{\rm{\pi }}f}} = \frac{{ - {\rm{j4\pi }}f}}{{\varepsilon ^2 + \left( {2{\rm{\pi }}f} \right)^2 }}.$$ | + | :$$X_\varepsilon (f) = \frac{1}{ {\varepsilon + {\rm{j} }2{\rm{\pi } }f} } - \frac{1}{ {\varepsilon - {\rm{j} }2{\rm{\pi } }f} } = \frac{ { - {\rm{j4\pi } }f} }{ {\varepsilon ^2 + \left( {2{\rm{\pi } }f} \right)^2 } }.$$ |
| − | + | But actually we are interested in the spectrum of the »jump function« | |
| − | $$x(t) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm}\to \hspace{0.05cm}0 } x_\varepsilon (t).$$ | + | :$$x(t) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm}\to \hspace{0.05cm}0 } x_\varepsilon (t).$$ |
| − | + | Therefore, the spectral function $X(f) =\text{F}\big[x(t)\big]$ has to be determined as limit value of $X_\varepsilon(f)$ for $\varepsilon \to 0$: | |
| − | $$X(f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 } X_\varepsilon (f) = \frac{{ - {\rm{j}}}}{{{\rm{\pi }}f}} = \frac{1}{{{\rm{j\pi }}f}}.$$ | + | :$$X(f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 } X_\varepsilon (f) = \frac{ { - {\rm{j} } } }{ { {\rm{\pi } }f} } = \frac{1}{ { {\rm{j\pi } }f} }.$$ |
| − | |||
| − | |||
| − | |||
| − | $ | + | In the right graph the imaginary spectral function $X(f)$ is shown as a blue curve. You can see that $\vert X(f) \vert$ decreases continuously with increasing frequency. |
| − | |||
| − | |||
| − | + | ⇒ The green curve in the left graph shows the signal $y(t)$, which differs from $x(t)$ only in the negative time section. | |
| + | *In this area $y(t) = 0$. The corresponding spectral function $Y(f)$ is only half as large as $X(f)$ in the entire range. This is shown in the following calculation: | ||
| − | == | + | :$$Y(f) = \mathop {\lim }\limits_{\varepsilon \to 0 } Y_\varepsilon (f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 }\frac{1}{ {\varepsilon + {\rm{j} }2{\rm{\pi } }f} } = \frac{1}{ { {\rm{j2\pi } }f} }.$$ |
| + | |||
| + | *In addition there is a Dirac delta function at $f = 0$ with weight $1/2$, due to the equal part. This is explained in the example in section [[Signal_Representation/Fourier_Transform_Theorems#Assignment_Theorem|»Assignment Theorem«]]. }} | ||
| − | |||
| − | [[File: | + | ==The second Fourier integral== |
| + | <br> | ||
| + | Up to now, it has only been shown how to calculate the corresponding spectral function $X(f)$ for an aperiodic, pulse-like signal $x(t)$. | ||
| + | [[File:EN_Sig_T_3_1_S7.png|right|frame|On the second Fourier integral]] | ||
| + | Now we turn to the reverse task, namely: How to determine the time function $x(t)$ from the spectral function $X(f)$? | ||
| − | + | With the same designations as in the first sections of this chapter, you can write the signal $x(t)$ as Fourier series, where now the limit ${f_0}' \to 0$ is to be considered: | |
| − | $$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty}{D_{\it \nu}}' \cdot \rm e^{j 2 \pi \it\nu {f_{\rm 0}}' t}.$$ | + | :$$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty}{D_{\it \nu}}' \cdot \rm e^{j\hspace{0.03cm} 2 \hspace{0.03cm}\pi \hspace{0.03cm}\it\nu \hspace{0.03cm} {f_{\rm 0}}' t}.$$ |
| − | + | If you extend both the numerator and the denominator by ${f_0}'$, you get | |
| − | $$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty} ({{D_{\it \nu}}'}/{{f_{\rm 0}}'}) \cdot \rm e^{j 2 \pi \it \nu {f_{\rm 0}}' t} \cdot {\it f_{\rm 0}}'.$$ | + | :$$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty} ({{D_{\it \nu}}'}/{{f_{\rm 0}}'}) \cdot \rm e^{j \hspace{0.03cm}2\hspace{0.03cm} \pi \hspace{0.03cm} \it \nu \hspace{0.03cm}{f_{\rm 0}}' t} \cdot {\it f_{\rm 0}}'.$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The limit crossing ${f_0}' \to 0$ has the following effects: | |
| + | #The $($infinite$)$ sum becomes an integral, where ${f_0}'$ has to be formally replaced by the differential quantity $\text{d}f$ $($integration variable$)$. | ||
| + | #The quantity $\nu \cdot{f_0}'$ in the exponent describes the physical frequency $f$. | ||
| + | #The quotient ${D_{\nu}}'/{f_0}'$ yields the spectral function $X(f)$ at the frequency $f$. | ||
| − | |||
| − | |||
| − | + | Taking these properties into account, the »second Fourier integral« is obtained. | |
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Second Fourier Integral:}$ If the spectral function $X(f)$ of an aperiodic and energy-limited signal is given, then the corresponding »'''time signal'''« is: | ||
| − | {{ | + | :$$x(t) = \hspace{0.01cm}\int_{-\infty} ^{ {+}\infty} X(f) \, \cdot \, { \rm e}^{\rm j 2\pi \it ft} \,{\rm d}f.$$}} |
| − | |||
| − | [[Aufgaben:3.1 | + | ==Exercises for the Chapter== |
| + | <br> | ||
| + | [[Aufgaben:Exercise_3.1:_Spectrum_of_the_Exponential_Pulse|Exercise 3.1: Spectrum of the Exponential Pulse]] | ||
| − | [[Aufgaben:3. | + | [[Aufgaben:Exercise_3.1Z:_Spectrum_of_the_Triangular_Pulse| Exercise 3.1Z: Spectrum of the Triangular Pulse]] |
| − | |||
| − | + | [[Aufgaben:Exercise_3.2:_From_the_Spectrum_to_the_Signal|Exercise 3.2: From the Spectrum to the Signal]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[Aufgaben:Exercise_3.2Z:_Sinc-Squared-Spectrum_with_Diracs| Exercise 3.2Z: Sinc–Squared Spectrum with Diracs]] | ||
{{Display}} | {{Display}} | ||
Latest revision as of 13:38, 14 June 2023
Contents
# OVERVIEW OF THE THIRD MAIN CHAPTER #
In the second chapter periodic signals were described by different harmonic oscillations (»Fourier series«).
If one reduces – at least mentally – the repetition frequency of a periodic signal more and more, i.e., the period duration becomes longer and longer, then one comes from the periodic signal to the unique »aperiodic signal« – often also called »pulse«.
In the following, such aperiodic and pulse–shaped signals are considered and mathematically described in the time and frequency domain.
The chapter contains in detail:
- The derivation of the two »Fourier integrals« from the Fourier series,
- the extension of the Fourier integral to the »Fourier transform« by means of distributions,
- »some special cases« of pulses: »rectangular pulse« and »Gaussian pulse«,
- the »laws of Fourier transform«, and finally
- the meaning of the »convolution operation« and its various applications.
»Laplace transform« and »Hilbert transform«, which are only applicable to causal signals or systems, will be treated in the second book »Linear Time-invariant Systems«.
Properties of aperiodic signals
In the last chapter periodic signals were considered. The essential characteristic of these signals is, that you can specify a period duration $T_0$ for them. If such a period duration cannot be indicated or – which is the same in practice – has an infinitely large value $T_0$, one speaks of an »aperiodic signal«.
For the present chapter »Aperiodic Signals – Pulses» the following conditions should apply:
- The considered signals $x(t)$ are aperiodic and "energy-limited": They possess a finite energy $E_x$ and a negligible $($medium$)$ power $P_x$.
- Often the energy of these signals is concentrated on a relatively short time range, so that one also speaks of »pulse-like signals« or »pulses«.
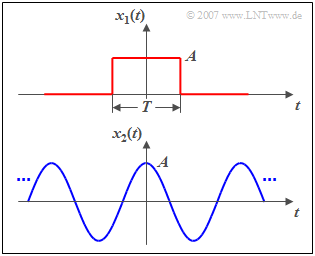
$\text{Example 1:}$ The figure shows a rectangular pulse $x_1(t)$ with amplitude $A$ and duration $T$ as an example of an aperiodic and time-limited signal. This pulse has
- the finite signal energy ⇒ here: $E_1=A^2 \cdot T$, and
- the power $P_1=0$.
A power-limited signal, for example the cosine signal $x_2(t)$ shown below, has
- always a finite power ⇒ here: $P_2=A^2/2$, and
- thus also an infinitely large signal energy: $E_2 \to \infty$.
Closer examination of the Fourier coefficients
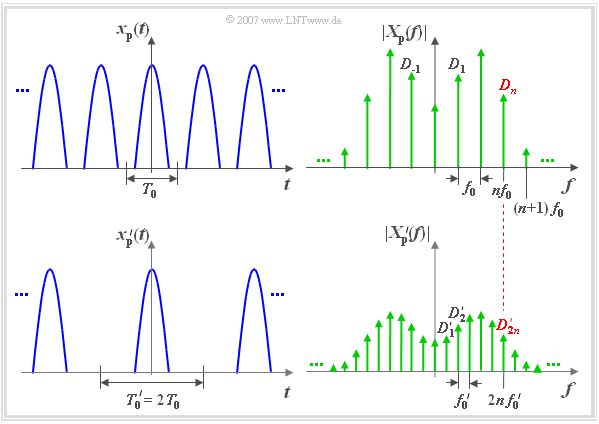
We assume a periodic signal $x_{\rm P}(t)$ with period duration $T_0$ which corresponds to the explanations in section »Complex Fourier series«.
- This signal can be described as follows:
- $$x_{\rm P}(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j 2 \pi \hspace{0.01cm}{\it n} \hspace{0.01cm}\it t / T_{\rm 0}}.$$
- The Fourier coefficients are generally complex $($with $D_{-n}=D_n^\ast)$:
- $$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{0.01cm}{\it n} \it t / T_{\rm 0}}\, {\rm d}t.$$
- The corresponding spectral function $X_{\rm P}(f)$ is a »line spectrum« with spectral lines in the distance $f_0=1/T_0$:
- $$X_{\rm P}(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$
- The upper figure shows on the left the periodic time signal $x_{\rm P}(t)$ and on the right the corresponding magnitude spectrum $|X_{\rm P}(f)|$. This is merely a schematic sketch.
- If $x_{\rm P}(t)$ is a real and even function, then $X_{\rm P}(f)$ is also real and even. The equation $X_{\rm P}(f) = |X_{\rm P}(f)|$ is only valid if all spectral lines are positive.
In the lower figure on the left side another periodic signal ${x_{\rm P}}\hspace{0.01cm}'(t)$ with double period duration ${T_0}\hspace{0.01cm}' = 2 \cdot T_0$ is displayed. The following applies to this signal:
- $${x_{\rm P}}'(t)=\sum^{+\infty}_{n=-\infty}{\it D_n}'\cdot {\rm e}^{{\rm j} 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}\hspace{0.01cm}'} \hspace{0.3cm}{\rm with}\hspace{0.3cm}{\it D_n}'=\frac{1}{{T_0}\hspace{0.01cm}'}\cdot \int^{{+T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}\hspace{0.01cm}'}\, {\rm d}\it t.$$
In the range from $-T_0/2$ to $+T_0/2$ the two signals $x_{\rm P}(t)$ and $x_{\rm P}\hspace{0.01cm}'(t)$ are identical.
We will also consider the spectral function ${X_{\rm P} }'(f)$ according to the right sketch:
- Due to the double period duration $({T_0}' = 2 \cdot T_0)$ the spectral lines are now closer together $({f_0}' = f_0/2)$.
- Both red marked coefficients $D_n$ und ${D_{2n}}'$ belong to the same physical frequency $f = n \cdot f_0 = 2n \cdot {f_0}'$.
We recognize by a comparison of the two coefficients
- $$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} \it t / T_{\rm 0}}\, {\rm d}t \hspace{0.5cm}\text{and} \hspace{0.5cm} {D_{2n}}'=\frac{1}{{T_0}'}\cdot \int^{+{T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 4 \pi \hspace{-0.05cm}{\it n} \it t / {T_{\rm 0}}'}\, {\rm d}t \text{:} $$
- ${x_{\rm P}}'(t) \equiv 0$ between $T_0/2$ and ${T_0}'/2$ and also in a symmetrical interval for negative times.
- Therefore the integration limits can be restricted to $\pm T_0/2$.
- Inside the new integration limits: ${x_{\rm P}}'(t)$ can be replaced by $x_{\rm P}(t)$.
- If we set ${T_0}' = 2T_0$ in the above equation, we get:
- $${D_{2n}}'=\frac{1}{2T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} t / T_{\rm 0}}\, {\rm d}t = {D_n}/{2} .$$
$\text{We summarize this result briefly:}$
- The spectral line of the signal ${x_{\rm P} }'(t)$ at frequency $f = n \cdot {f_0}'$ is denoted by ${D_{2n} }'$ $($see lower graph on the right$)$.
- This line has exactly half the size of the spectral line $D_n$ of the signal $x_{\rm P}(t)$ at the same physical frequency $f$ $($see upper graph on the right$)$.
- The spectral function ${X_{\rm P} }'(f)$ has opposite $X_{\rm P}(f)$ additional spectral lines at $(n + 1/2) \cdot f_0$ $($see lower graph on the left$)$.
- These additional lines lead to the fact that in the time domain every second pulse of $x_{\rm P}(t)$ – located by $n \cdot T_0$ $(n$ odd$)$ – is cancelled.
From the periodic to the aperiodic signal
We now take up the considerations in the previous section and select the period duration ${T_0}'$ of ${x_{\rm P}}'(t)$ generally by an integer factor $k$ greater than the period duration $T_0$ of ${x_{\rm P}}(t)$. Then the previous statements can be generalized:
- The line spacing is smaller for ${X_{\rm P}}'(f)$ by the factor $k$ than for the spectrum ${X_{\rm P}}(f)$.
- To emphasize this fact, we denote the discrete frequency variable of function ${X_{\rm P}}'(f)$ with $\nu$ instead of $n$. The following applies:
- $$\nu=k \cdot n.$$
- It applies for the red marked spectral line of signal ${x_{\rm P}}'(t)$ at frequency $f=n \cdot f_0 =\nu \cdot {f_0}'$:
- $${D_\nu}' = {1}/{k} \cdot D_n.$$
- If one now chooses – as shown schematically in the graph – the factor $k$ and thus the period duration ${T_0}'$ always larger and finally lets it go to infinity, then
- the periodic signal ${x_{\rm P}}(t)$ changes to the aperiodic signal $x(t)$,
- the line spectrum ${X_{\rm P}}(f)$ can be replaced by the continuous spectrum $X(f)$.
The first Fourier integral
Concerning the spectral functions $X_{\rm P}(f)$ and $X(f)$ the following statements can be made:
- The individual spectral lines now lie as close together as desired $({f_0}'=1/{T_0}' \to 0)$.
- In the spectral function $X(f)$ all possible $($not only discrete$)$ frequencies now occur within certain intervals ⇒ $X(f)$ is no longer a line spectrum.
- The contribution of each individual frequency $f$ to the signal $x(t)$ is negligibly small $(k \to \infty,\ {D_{\nu}}' \to 0)$.
- Because of the infinite number of frequencies there is a finite result in total.
- Instead of calculating the Fourier coefficients ${D_{\nu}}'$: Now a spectral density $X(f)$ is calculated. For the frequency $f=\nu\cdot {f_0}'$ then applies:
- $$X(f = {\rm \nu} {f_{\rm 0}}') = \lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm} 0} ({{D_{\rm \nu}}'}/{{f_{\rm 0}}'}) = \lim_{{T_{\rm 0}}' \to \infty} ({D_{\rm \nu}}' \cdot {T_{\rm 0}}').$$
- The spectral function $X(f)$ of the aperiodic signal $x(t)$ is visible in the spectrum $X_{\rm P}(f)$ of the periodic signal $x_{\rm P}(t)$ as envelope $($see graphics in the last section$)$.
- In the lower graphic ${D_{\nu}}'$ corresponds to the red-shaded area of the frequency interval around $\nu \cdot {f_0}'$ with width ${f_0}'$.
If you use the equations given in the last section, you get
- $$X(f = {\rm \nu} \cdot {f_{\rm 0}}') = \lim_{{T_{\rm 0}'} \to \infty} \int ^{{T_{\rm 0}}'/2} _{-{T_{\rm 0}}'/2} x_{\rm P}(t) \, \cdot \, { \rm e}^{-\rm j 2\pi\nu \it {f_{\rm 0}}' t} \,{\rm d}t.$$
Through the common limit crossing $({T_0}' \to \infty, \ {f_0}' \to 0)$ the following transformations will happen:
- From the periodic signal $x_{\rm P}(t)$ to the aperiodic signal $x(t)$.
- From the discrete frequency $\nu \cdot {f_0}'$ to the continuous frequency variable $f$.
Thus, a fundamental definition is obtained, which allows the calculation of the spectral function of an aperiodic time function. The name of this spectral transformation goes back to the French physicist »$\text{Jean-Baptiste Joseph Fourier}$«.
$\text{First Fourier Integral:}$
The »spectral function« $($or short: the »spectrum«$)$ of an aperiodic and simultaneously energy limited signal $x(t)$ is to be calculated as follows
- $$X(f)= \hspace{0.05cm}\int_{-\infty} ^{ {+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$
The following $($German language$)$ learning video should clarify the statements of the last sections:
»Kontinuierliche und diskrete Spektren« ⇒ "Continuous and discrete spectra".
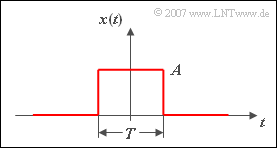
$\text{Example 2:}$ Given is the sketched time course $x(t)$. The corresponding spectrum $X(f)$ is searched for using the first Fourier integral:
- From the above representation we can see, that for $\vert t \vert > T/2$ the signal is $x(t) = 0$.
- This means that the integration interval can be limited to the range $\pm T/2$.
- This results in the approach:
- $$ \begin{align*} X(f) & = A \cdot \int_{- T/2}^{+T/2} {\rm e}^{- {\rm j2\pi} ft}\,{\rm d}t = \frac{ A}{- \rm j2\pi f}\left[ {\rm e}^{- {\rm j}2\pi ft}\right]_{-T/2}^{+T/2} \\ & = \frac{\it A} {- \rm j 2\pi f}\cdot \big[\cos({\rm \pi} f T) - {\rm j} \cdot \sin({\rm \pi} fT) - \cos({\rm \pi} fT) - {\rm j} \cdot \sin({\rm \pi} fT)\big] \end{align*}$$
- $$\Rightarrow \hspace{0.5cm}X(f)=A\cdot \frac{\sin({\rm \pi} fT)}{ {\rm \pi} f},$$
- If you extend numerator and denominator with $T$, you get:
- $$X(f)=A\cdot T \cdot\frac{\sin(\pi fT)}{\pi fT} = A\cdot T \cdot{\rm si }(\pi fT) = A\cdot T \cdot{\rm sinc }(fT).$$
$\text{Definitions:}$ For abbreviation we define the following functions:
- »sinc–function« $($predominantly used in Anglo-American literature$)$
- $${\rm sinc}( x ) = {\sin (\pi x) }/(\pi x ),$$
- »si–function« or »$\text{splitting function}$« $($predominantly used in German literature$)$
- $${\rm si}\left( x \right) = \sin \left( x \right)/x = {\rm sinc}(x/\pi ).$$
Note: In our $\rm LNTwww$ we mostly use the function ${\rm si}(x)$, but important results are also given in the ${\rm sinc}(x)$ form.
Fourier transform
The spectrum $X(f)$ of a signal $x(t)$ is according to the »first Fourier integral«:
- $$X(f)= \hspace{0.05cm}\int _{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$
As shown in the last section with a simple example, this integral can be solved easily for an energy-limited signal $x(t)$. For non-energy limited signals, for example
- a »DC signal«, or
we observe a divergence of the Fourier integral. Including a bilateral declining auxiliary function $\varepsilon (t)$, however, convergence can be forced:
- $$X(f) = \lim_{\varepsilon \to 0} \int _{-\infty} ^{{+}\infty} x(t) \cdot {\rm e}^{\it -\varepsilon | \hspace{0.01cm} t \hspace{0.01cm} |} \cdot {\rm e}^{{-\rm j 2 \pi}\it ft} \,{\rm d}t.$$
Such non-energy limited signals lead to so-called »Dirac delta functions« in the spectral domain, sometimes also called »distributions«.
$\text{Definition:}$ The generally valid functional relation $X(f) = F\big [x(t) \big ]$ is called »Fourier Transform«. For the short notation we use $($with the "white dot" for the time domain and the "filled dot" for the spectral domain$)$:
- $$X(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x(t).$$
With a increasing signal, however, convergence is only achieved as long as the time function increases less than exponentially.
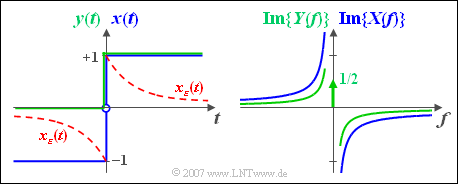
$\text{Example 3:}$ We consider an acausal jump function
- $$x (t) = \left\{ {\begin{array}{*{20}c} { +1 } & { {\rm{for} }\quad t > 0,} \\ {-1 } & { {\rm{for} }\quad t < 0.} \\\end{array} } \right.$$
This signal is shown in blue color in the left sketch.
Since the signal $x(t)$ extends to infinity on both sides, we must add a suitable convergence factor $\text{e}^{-\varepsilon \hspace{0.05cm} \cdot \hspace{0.05cm}\vert \hspace{0.05cm} t \hspace{0.05cm} \vert}$ with $($ $\varepsilon > 0)$ in order to calculate the Fourier transform for both sections. The resulting time function is then
- $$x_\varepsilon (t) = \left\{ {\begin{array}{*{20}c} { {\rm{e} }^{ - \varepsilon \hspace{0.05cm} \cdot \hspace{0.05cm}t} } & { {\rm{for} }\quad t > 0,} \\ { {\rm{ - e} }^{\hspace{0.05cm}\varepsilon\hspace{0.05cm} \cdot \hspace{0.05cm} t} } & { {\rm{for} }\quad t < 0.} \\\end{array} } \right.$$
Following a similar procedure as in section »Dirac delta function in the frequency domain« results for the corresponding spectral function:
- $$X_\varepsilon (f) = \frac{1}{ {\varepsilon + {\rm{j} }2{\rm{\pi } }f} } - \frac{1}{ {\varepsilon - {\rm{j} }2{\rm{\pi } }f} } = \frac{ { - {\rm{j4\pi } }f} }{ {\varepsilon ^2 + \left( {2{\rm{\pi } }f} \right)^2 } }.$$
But actually we are interested in the spectrum of the »jump function«
- $$x(t) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm}\to \hspace{0.05cm}0 } x_\varepsilon (t).$$
Therefore, the spectral function $X(f) =\text{F}\big[x(t)\big]$ has to be determined as limit value of $X_\varepsilon(f)$ for $\varepsilon \to 0$:
- $$X(f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 } X_\varepsilon (f) = \frac{ { - {\rm{j} } } }{ { {\rm{\pi } }f} } = \frac{1}{ { {\rm{j\pi } }f} }.$$
In the right graph the imaginary spectral function $X(f)$ is shown as a blue curve. You can see that $\vert X(f) \vert$ decreases continuously with increasing frequency.
⇒ The green curve in the left graph shows the signal $y(t)$, which differs from $x(t)$ only in the negative time section.
- In this area $y(t) = 0$. The corresponding spectral function $Y(f)$ is only half as large as $X(f)$ in the entire range. This is shown in the following calculation:
- $$Y(f) = \mathop {\lim }\limits_{\varepsilon \to 0 } Y_\varepsilon (f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 }\frac{1}{ {\varepsilon + {\rm{j} }2{\rm{\pi } }f} } = \frac{1}{ { {\rm{j2\pi } }f} }.$$
- In addition there is a Dirac delta function at $f = 0$ with weight $1/2$, due to the equal part. This is explained in the example in section »Assignment Theorem«.
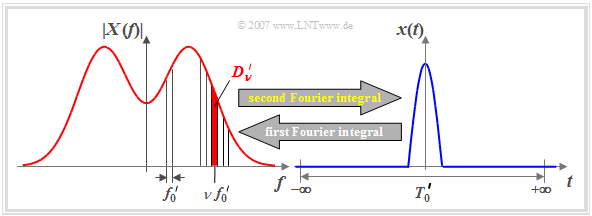
The second Fourier integral
Up to now, it has only been shown how to calculate the corresponding spectral function $X(f)$ for an aperiodic, pulse-like signal $x(t)$.
Now we turn to the reverse task, namely: How to determine the time function $x(t)$ from the spectral function $X(f)$?
With the same designations as in the first sections of this chapter, you can write the signal $x(t)$ as Fourier series, where now the limit ${f_0}' \to 0$ is to be considered:
- $$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty}{D_{\it \nu}}' \cdot \rm e^{j\hspace{0.03cm} 2 \hspace{0.03cm}\pi \hspace{0.03cm}\it\nu \hspace{0.03cm} {f_{\rm 0}}' t}.$$
If you extend both the numerator and the denominator by ${f_0}'$, you get
- $$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty} ({{D_{\it \nu}}'}/{{f_{\rm 0}}'}) \cdot \rm e^{j \hspace{0.03cm}2\hspace{0.03cm} \pi \hspace{0.03cm} \it \nu \hspace{0.03cm}{f_{\rm 0}}' t} \cdot {\it f_{\rm 0}}'.$$
The limit crossing ${f_0}' \to 0$ has the following effects:
- The $($infinite$)$ sum becomes an integral, where ${f_0}'$ has to be formally replaced by the differential quantity $\text{d}f$ $($integration variable$)$.
- The quantity $\nu \cdot{f_0}'$ in the exponent describes the physical frequency $f$.
- The quotient ${D_{\nu}}'/{f_0}'$ yields the spectral function $X(f)$ at the frequency $f$.
Taking these properties into account, the »second Fourier integral« is obtained.
$\text{Second Fourier Integral:}$ If the spectral function $X(f)$ of an aperiodic and energy-limited signal is given, then the corresponding »time signal« is:
- $$x(t) = \hspace{0.01cm}\int_{-\infty} ^{ {+}\infty} X(f) \, \cdot \, { \rm e}^{\rm j 2\pi \it ft} \,{\rm d}f.$$
Exercises for the Chapter
Exercise 3.1: Spectrum of the Exponential Pulse
Exercise 3.1Z: Spectrum of the Triangular Pulse
Exercise 3.2: From the Spectrum to the Signal
Exercise 3.2Z: Sinc–Squared Spectrum with Diracs