Contents
# OVERVIEW OF THE THIRD MAIN CHAPTER #
In the second chapter periodic signals were described by different harmonic oscillations („fourier series”). If one reduces – at least mentally – the pulse repetition frequency of a periodic signal more and more, i.e., the period duration becomes longer and longer, then one comes from the periodic signal (pulse) to the unique aperiodic signal – often also called pulse .
In the following, such aperiodic, impulse-shaped signals are considered and mathematically described in the time– and frequency domain.
The chapter contains in detail:
- the derivation of the two fourier integral from the fourier series
- the extension of the Fourier integral to fourier transform by means of distributions,
- some special cases impulse-like signals like square–, Gauss– and Diracimpulse,
- the laws of the fourier transform, and finally
- the meaning of the convolution operation and its various applications.
The Laplace– and the Hilbert transform, which are only applicable to causal signals or systems, will be treated in the next book „Linear time-invariant systems”.
Further information on the topic as well as tasks, simulations and programming exercises can be found in the
- Chapter 6: Linear time-invariant systems, Program lzi
of the lab „Simulation Methods in Communication Engineering”. This (former) LNT course at the TU Munich is based on
- the educational software package LNTsim ⇒ Link points to the ZIP version of the program and
- the associated lab description ⇒ Link refers to the PDF version; Chapter 6: pages 99-118.
Properties of aperiodic signals
In the last chapter periodic signals were considered. The essential characteristic of these signals is, that you can specify a period duration $T_0$ for them. If such a period duration cannot be indicated or - which is the same in practice - has $T_0$ an infinitely large value, one speaks of an 'aperiodic signal.
For the present chapter „Aperiodic Signals – Impulse” the following conditions should apply:
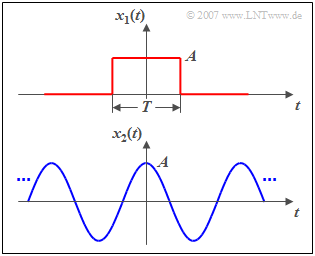
- The considered signals $x(t)$ are aperiodic and energy-limited: They possess a finite energy $E_x$ and a negligible (medium) power $P_x$.
- Often the energy of these signals is concentrated on a relatively short time range, so that one also speaks of impulse-shaped signals .
$\text{Example 1:}$ The figure above shows a rectangular pulse $x_1(t)$ with amplitude $A$ and duration $T$ as an example of an aperiodic and time-limited signal. This pulse has
- the finite signal-energy ⇒ here: $E_1=A^2 \cdot T$, and
- the power $P_1$ = 0.
A power-limited signal, for example the cosine signal $x_2(t)$, shown below, has
- always a finite power ⇒ here: $P_2=A^2/2$, and
- thus also an infinitely large signal energy: $E_2 \to \infty$.
Closer Examination of the Fourier Coefficients
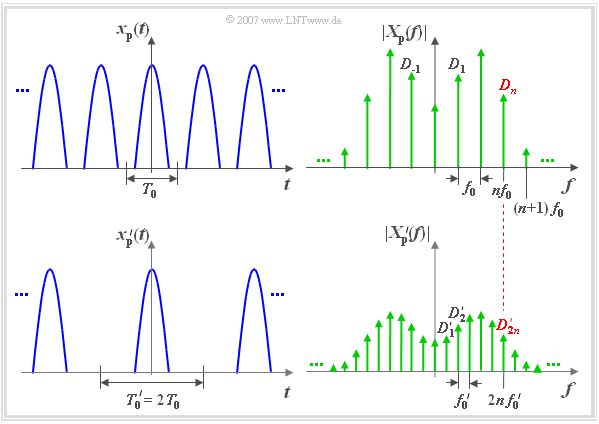
We assume a periodic signal $x_{\rm P}(t)$ with the period duration $T_0$ which corresponds to the explanations on the page Complex Fourier Series . This signal can be displayed as follows:
- $$x_{\rm P}(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j 2 \pi \hspace{0.01cm}{\it n} \hspace{0.01cm}\it t / T_{\rm 0}}.$$
- The Fourier coefficients are generally complex
$($it applies $D_{-n}={D_n}^\ast)$:
- $$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{0.01cm}{\it n} \it t / T_{\rm 0}}\, {\rm d}t.$$
- The corresponding spectral function $X_{\rm P}(f)$ is a so-called line spectrum with spectral lines in the distance $f_0=1/T_0$:
- $$X_{\rm P}(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$
The upper figure shows on the left the periodic time signal $x_{\rm P}(t)$ and on the right the corresponding magnitude spectrum $|X_{\rm P}(f)|$. This is merely a schematic sketch:
Further notes:
- If $x_{\rm P}(t)$ is a real and even function, then $X_{\rm P}(f)$ is also real and even.
- The equation $X_{\rm P}(f) = |X_{\rm P}(f)|$ is only valid if all spectral lines are positive.
In the lower figure on the left side another periodic signal ${x_{\rm P}}\hspace{0.01cm}'(t)$ with double period duration ${T_0}\hspace{0.01cm}' = 2 \cdot T_0$ is displayed. The following applies to this signal:
- $${x_{\rm P}}'(t)=\sum^{+\infty}_{n=-\infty}{\it D_n}'\cdot {\rm e}^{{\rm j} 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}\hspace{0.01cm}'} \hspace{0.3cm}{\rm mit}\hspace{0.3cm}{\it D_n}'=\frac{1}{{T_0}\hspace{0.01cm}'}\cdot \int^{{+T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}\hspace{0.01cm}'}\, {\rm d}\it t.$$
In the range from $-T_0/2$ to $+T_0/2$ the two signals are identical. We will also consider the spectral function ${X_{\rm P} }'(f)$ according to the right sketch:
- Due to the double period duration $({T_0}' = 2 \cdot T_0)$ the spectral lines are now closer together $({f_0}' = f_0/2)$.
- Both red marked coefficients $D_n$ und ${D_{2n}}'$ belong to the same physical frequency $f = n \cdot f_0 = 2n \cdot {f_0}'$.
We recognize by a comparison of the two coefficients
- $$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} \it t / T_{\rm 0}}\, {\rm d}t \hspace{0.5cm}\text{und} \hspace{0.5cm} {D_{2n}}'=\frac{1}{{T_0}'}\cdot \int^{+{T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 4 \pi \hspace{-0.05cm}{\it n} \it t / {T_{\rm 0}}'}\, {\rm d}t \text{:} $$
- ${x_{\rm P}}'(t) \equiv 0$ betweeen $T_0/2$ and ${T_0}'/2$ ist also in a symmetrical interval for negative times.
- Therefore the integration limits can be restricted to $\pm T_0/2$ .
- Inside the new integration limits ${x_{\rm P}}'(t)$ can be replaced by $x_{\rm P}(t)$ .
If we now set ${T_0}' = 2T_0$ in the above equation, we get
- $${D_{2n}}'=\frac{1}{2T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} t / T_{\rm 0}}\, {\rm d}t = {D_n}/{2} .$$
$\text{We summarize this result briefly:}$
- The spectral line of the signal ${x_{\rm P} }'(t)$ at frequency $f = n \cdot {f_0}'$ is denoted by ${D_{2n} }'$ (lower graph).
- This line is exactly half the size of the spectral line $D_n$ of the signal $x_{\rm P}(t)$ at the same physical frequency $f$ (upper graph).
- The spectral function ${X_{\rm P} }'(f)$ has opposite $X_P(f)$ additional spectral lines at $(n + 1/2) \cdot f_0$ .
- These lead to the fact that in the time domain every second „impulse” of $x_{\rm P}(t)$ um $n \cdot T_0$ located $(n$ odd$)$ is erased.
From the Periodic to the Aperiodic Signal
We now take up the considerations on the previous page and select the period duration ${T_0}'$ of ${x_{\rm P}}'(t)$ generally by an integer factor $k$ greater than the period duration $T_0$ of ${x_{\rm P}}(t)$. Then the previous statements can be generalized:
- The line spacing is smaller for ${X_{\rm P}}'(f)$ by the factor $k$ than for spectrum ${X_{\rm P}}(f)$.
- To emphasize this fact, we denote the frequency–running variable of function ${X_{\rm P}}'(f)$ with $\nu$ instead of $n$. The following applies: $\nu=k \cdot n$.
- For the spectral line of the signal ${x_{\rm P}}'(t)$ at the frequency $f=n \cdot f_0 =\nu \cdot {f_0}'$ applies:
$${D_\nu}' = {1}/{k} \cdot D_n, \hspace{0.5cm} {\rm where} \hspace{0.5cm} \nu = k \cdot n.$ If one now chooses - as shown schematically in the picture - the factor $k$ and thus the period duration ${T_0}'$ always larger and finally lets it go to infinity, then * the periodic signal ${x_{\rm P}}(t)$ changes to the aperiodic signal $x(t)$ , *the line spectrum ${X_{\rm P}}(f)$ can be replaced by the continuous spectrum $X(f)$ . <br clear="all"> =='"`UNIQ--h-4--QINU`"'The First Fourier Integral== <br> Concerning the spectral function $X_{\rm P}(f)$ and $X(f)$ the following statements can be made: *The individual spectral lines now lie as close together as desired $({f_0}'=1/{T_0}' \to 0)$. *In the spectral function $X(f)$ all possible (not only discrete) frequencies now occur within certain intervals ⇒ $X(f)$ is no longer a line spectrum. *The contribution of each individual frequency $f$ to the signal is only negligibly small $(k \to \infty, {D_{\nu}}' \to 0)$. *Because of the infinite number of frequencies there is a finite result in total. *Instead of calculating the Fourier coefficients ${D_{\nu}}'$ a spectral density $X(f)$ is now calculated. For the frequency $f=\nu\cdot {f_0}'$ then applies: : $$X(f = {\rm \nu} {f_{\rm 0}}') = \lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm} 0} ({{D_{\rm \nu}}'}/{{f_{\rm 0}}'}) = \lim_{{T_{\rm 0}}' \to \infty} ({D_{\rm \nu}}' \cdot {T_{\rm 0}}').$$ *The spectral function $X(f)$ of the aperiodic signal $x(t)$ is visible in the spectrum $X_{\rm P}(f)$ of the periodic signal $x_{\rm P}(t)$ as envelope (see graphics). *In the lower graphic on the last page ${D_{\nu}}'$ corresponds to the red-shaded area of the frequency interval around $\nu \cdot {f_0}'$ with the width ${f_0}'$. If you use the equations given on the last page, you get :$$X(f = {\rm \nu} \cdot {f_{\rm 0}}') = \lim_{{T_{\rm 0}'} \to \infty} \int ^{{T_{\rm 0}}'/2} _{-{T_{\rm 0}}'/2} x_{\rm P}(t) \, \cdot \, { \rm e}^{-\rm j 2\pi\nu \it {f_{\rm 0}}' t} \,{\rm d}t.$$ Through the common limit crossing $({T_0}' \to \infty, \ {f_0}' \to 0)$ the following transformations will happen *from the periodic signal $x_{\rm P}(t)$ the aperiodic signal $x(t)$, and *from the discrete frequency $\nu \cdot {f_0}'$ the continuous frequency variable $f$. Thus, a fundamental definition is obtained, which allows the calculation of the spectral function of an aperiodic time function. The name of this spectral transformation goes back to the French physicist [https://en.wikipedia.org/wiki/Joseph_Fourier Jean-Baptiste-Joseph Fourier] . <div class="bluebox"> $\text{First Fourier Integral:}$ The '''spectral function''' (or short: the ''spectrum'' ) of an aperiodic and simultaneously energy limited signal $x(t)$ is to be calculated as follows :$$X(f)= \hspace{0.05cm}\int_{-\infty} ^{ {+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$ <div style="clear:both;"> </div> </div> The german learning video [[Kontinuierliche_und_diskrete_Spektren_(Lernvideo)|Continuous and discrete Spectr]] should clarify the statements of the last pages. [[File:P_ID330__Sig_T_3_1_S5_neu.png|right|frame|Rectangular Pulse $x(t)$]] <div class="greybox"> $\text{Example 2:}$ Given is the sketched time course $x(t)$. The corresponding spectrum is searched for $X(f)$. For this we use the first Fourier integral. *From the above representation we can see, that for $\vert t \vert > T/2$ the signal $x(t) = 0$ is *This means that the integration interval can be limited to the range $\pm T/2$ . *This results in the approach: :$$ \begin{align*} X(f) & = A \cdot \int_{- T/2}^{+T/2} {\rm e}^{- {\rm j2\pi} ft}\,{\rm d}t = \frac{ A}{- \rm j2\pi f}\left[ {\rm e}^{- {\rm j}2\pi ft}\right]_{-T/2}^{+T/2} \\ & = \frac{\it A} {- \rm j 2\pi f}\cdot \big[\cos({\rm \pi} f T) - {\rm j} \cdot \sin({\rm \pi} fT) - \cos({\rm \pi} fT) - {\rm j} \cdot \sin({\rm \pi} fT)\big] \end{align*}$$ :$$\Rightarrow \hspace{0.5cm}X(f)=A\cdot \frac{\sin({\rm \pi} fT)}{ {\rm \pi} f}.$$ *If you extend numerator and denominator with $T$, you get :$$X(f)=A\cdot T \cdot\frac{\sin(\pi fT)}{\pi fT} = A\cdot T \cdot{\rm si }(\pi fT) .$$ The function $\text{si}(x) = \sin(x)/x$ will be explained thoughtfully on the page [[Signal_Representation/Einige_Sonderf%C3%A4lle_impulsartiger_Signale#Rechteckimpuls|Rectangle Pulse]] . Man denotes this „si function” sometimes also as „splitting function”. <div style="clear:both;"> </div> </div> Betrachten wir noch die Einheiten der beiden Funktionen im Zeit- und Frequenzbereich: *Ist $x(t)$ beispielsweise eine Spannung, so hat die Impulsamplitude $A$ die Einheit „Volt”. *Die Dimension der Größe $T$ ist häufig die Zeit, zum Beispiel mit der Einheit „Sekunde”. *Der Kehrwert der Zeit entspricht der Frequenz mit der Einheit „Hertz”. *Das Argument $f \cdot T$ ist dimensionslos. *Die Spektralfunktion $X(f)$ hat somit beispielsweise die Einheit „V/Hz”. =='"`UNIQ--h-5--QINU`"'Fourier Transform== <br> Das Spektrum $X(f)$ eines Signals $x(t)$ lautet gemäß dem „Ersten Fourierintegral”: :$$X(f)= \hspace{0.05cm}\int _{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$ Wie auf der letzten Seite an einem einfachen Beispiel gezeigt wurde, ist dieses Integral bei einem energiebegrenzten Signal $x(t)$ problemlos lösbar. Bei nicht energiebegrenzten Signalen, zum Beispiel *einem [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal|Gleichsignal]] , *einer [[ Signal_Representation/Harmonic_Oscillation|harmonischen Schwingung]], oder *einem anklingenden Signal, divergiert aber das Fourierintegral. Unter Einbeziehung einer beidseitig abfallenden Hilfsfunkion $\varepsilon (t)$ kann allerdings die Konvergenz erzwungen werden: :$$X(f) = \lim_{\varepsilon \to 0} \int _{-\infty} ^{{+}\infty} x(t) \cdot {\rm e}^{\it -\varepsilon | \hspace{0.01cm} t \hspace{0.01cm} |} \cdot {\rm e}^{{-\rm j 2 \pi}\it ft} \,{\rm d}t.$$ Solche nicht energiebegrenzten Signale führen im Spektrum zu so genannten „Diracfunktionen”, manchmal auch „Distributionen” genannt. <div class="bluebox"> $\text{Definition:}$ Man bezeichnet den allgemein gültigen Funktionalzusammenhang $X(f) = F\big [x(t) \big ]$ als '''Fouriertransformation'''. Für die Kurzschreibweise verwenden wir (mit dem „weißen” Punkt für den Zeitbereich und dem ausgefüllten Punkt für den Spektralbereich): :$$X(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x(t).$$ Bei einem anklingenden Signal wird die Konvergenz allerdings nur dann erreicht, solange die Zeitfunktion weniger als exponentiell ansteigt. <div style="clear:both;"> </div> </div> [[File:P_ID655__Sig_T_3_1_S6.png|right|frame| Sprungfunktion und zugehöriges Spektrum]] <div class="greybox"> $\text{Beispiel 3:}$ Wir betrachten eine akausale Sprungfunktion :$$x (t) = \left\{ {\begin{array}{*{20}c} { +1 } & { {\rm{f\ddot{u}r} }\quad t > 0,} \\ {-1 } & { {\rm{f\ddot{u}r} }\quad t < 0.} \\\end{array} } \right.$$ Dieses Signal ist in der linken Skizze in blauer Farbe dargestellt. Da das Signal $x(t)$ nach beiden Seiten bis ins Unendliche reicht, muss zur Berechnung der Fouriertransformierten für beide Abschnitte zunächst ein geeigneter Konvergenzfaktor $\text{e}^{-\varepsilon \hspace{0.05cm} \cdot \hspace{0.05cm}\vert \hspace{0.05cm} t \hspace{0.05cm} \vert}$ hinzugefügt werden $($es gelte $\varepsilon > 0)$. Die resultierende Zeitfunktion lautet dann: :$$x_\varepsilon (t) = \left\{ {\begin{array}{*{20}c} { {\rm{e} }^{ - \varepsilon \hspace{0.05cm} \cdot \hspace{0.05cm}t} } & { {\rm{f\ddot{u}r} }\quad t > 0,} \\ { {\rm{ - e} }^{\hspace{0.05cm}\varepsilon\hspace{0.05cm} \cdot \hspace{0.05cm} t} } & { {\rm{f\ddot{u}r} }\quad t < 0.} \\\end{array} } \right.$$ Nach ähnlicher Vorgehensweise wie auf der Seite [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal#Diracfunktion_im_Frequenzbereich|Diracfunktion im Frequenzbereich]] ergibt sich für die zugehörige Spektralfunktion: :$$X_\varepsilon (f) = \frac{1}{ {\varepsilon + {\rm{j} }2{\rm{\pi } }f} } - \frac{1}{ {\varepsilon - {\rm{j} }2{\rm{\pi } }f} } = \frac{ { - {\rm{j4\pi } }f} }{ {\varepsilon ^2 + \left( {2{\rm{\pi } }f} \right)^2 } }.$$ Eigentlich interessieren wir uns aber für das Spektrum der tatsächlichen Sprungfunktion :$$x(t) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm}\to \hspace{0.05cm}0 } x_\varepsilon (t).$$ Deshalb ist auch die Spektralfunktion $X(f) =\text{F}\big[x(t)\big]$ als Grenzwert von $X_\varepsilon(f)$ für $\varepsilon \to 0$ zu bestimmen: :$$X(f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 } X_\varepsilon (f) = \frac{ { - {\rm{j} } } }{ { {\rm{\pi } }f} } = \frac{1}{ { {\rm{j\pi } }f} }.$$ In der rechten Grafik ist die imaginäre Spektralfunktion $X(f)$ als blaue Kurve dargestellt. Man erkennt, dass $\vert X(f) \vert$ mit steigender Frequenz kontinuierlich abnimmt. Der grüne Kurvenzug in der linken Grafik zeigt das Signal $y(t)$, das sich von $x(t)$ nur bei den negativen Zeiten unterscheidet. *In diesem Bereich gilt $y(t) = 0$. Die zugehörige Spektralfunktion $Y(f)$ ist im gesamten Bereich nur halb so groß wie $X(f)$. Dies zeigt die nachfolgende Rechnung: :$$Y(f) = \mathop {\lim }\limits_{\varepsilon \to 0 } Y_\varepsilon (f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 }\frac{1}{ {\varepsilon + {\rm{j} }2{\rm{\pi } }f} } = \frac{1}{ { {\rm{j2\pi } }f} }.$$ *Zudem ergibt sich auf Grund des Gleichanteils nun noch eine Diracfunktion bei $f = 0$ mit dem Gewicht $1/2$. Hierauf wird im Beispiel zum Abschnitt [[Signal_Representation/Fourier_Transform_Laws#Zuordnungssatz|Zuordnungssatz]] noch im Detail eingegangen. <div style="clear:both;"> </div> </div> ==Das zweite Fourierintegral== <br> Bisher wurde lediglich gezeigt, wie man für ein aperiodisches, impulsförmiges Signal $x(t)$ die zugehörige Spektralfunktion $X(f)$ berechnet. Nun wenden wir uns der umgekehrten Aufgabenstellung zu, nämlich: Wie ermittelt man die Zeitfunktion $x(t)$ aus der Spektralfunktion $X(f)$? [[File:P_ID399__Sig_T_3_1_S7_rah.png|center|frame|Zum zweiten Fourierintegral]] Mit den gleichen Bezeichnungen wie auf den ersten Seiten dieses Kapitels kann man das Signal $x(t)$ als Fourierreihe schreiben, wobei nun der Grenzübergang ${f_0}' \to 0$ zu berücksichtigen ist: :$$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty}{D_{\it \nu}}' \cdot \rm e^{j\hspace{0.03cm} 2 \hspace{0.03cm}\pi \hspace{0.03cm}\it\nu \hspace{0.03cm} {f_{\rm 0}}' t}.$$ Erweitert man nun sowohl den Zähler als auch den Nenner um ${f_0}'$, so erhält man: :$$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty} ({{D_{\it \nu}}'}/{{f_{\rm 0}}'}) \cdot \rm e^{j \hspace{0.03cm}2\hspace{0.03cm} \pi \hspace{0.03cm} \it \nu \hspace{0.03cm}{f_{\rm 0}}' t} \cdot {\it f_{\rm 0}}'.$$ Der Grenzübergang ${f_0}' \to 0$ hat folgende Auswirkungen: *Die (unendliche) Summe wird zu einem Integral, wobei ${f_0}'$ formal durch die differenzielle Größe $\text{d}f$ (Integrationsvariable) zu ersetzen ist. *Die Größe $\nu \cdot{f_0}'$ im Exponenten beschreibt die physikalische Frequenz $f$. *Der Quotient ${D_{\nu}}'/{f_0}'$ ergibt die Spektralfunktion $X(f)$ bei der Frequenz $f$. Unter Berücksichtigung dieser Eigenschaften kommt man zum „zweiten Fourierintegral”. <div class="bluebox"> $\text{Zweites Fourierintegral:}$ Ist die Spektralfunktion $X(f)$ eines aperiodischen und energiebegrenzten Signals gegeben, so lautet die dazugehörige '''Zeitfunktion''': :$$x(t) = \hspace{0.01cm}\int_{-\infty} ^{ {+}\infty} X(f) \, \cdot \, { \rm e}^{\rm j 2\pi \it ft} \,{\rm d}f.$$
Aufgaben zum Kapitel
Aufgabe 3.1: Spektrum des Exponentialimpulses
Aufgabe 3.1Z: Spektrum des Dreieckimpulses
Aufgabe 3.2: Vom Spektrum zum Signal
Aufgabe 3.2Z: si–Quadrat–Spektrum mit Diracs