Allgemeine Beschreibung der Binomialverteilung
Die Binomialverteilung stellt einen wichtigen Sonderfall für die Auftrittswahrscheinlichkeiten einer diskreten Zufallsgröße dar.
Zur Herleitung der Binomialverteilung gehen wir davon aus, dass $I$ binäre und statistisch voneinander unabhängige Zufallsgrößen $b_i$ den Wert „1” mit der Wahrscheinlichkeit Pr( $b_i =$ 0) $= p$ und den Wert „0” mit der Wahrscheinlichkeit Pr( $b_i =$ 1) $=$ 1 – $p$ annehmen kann. Dann ist die Summe $$z=\sum_{i=1}^{I}b_i$$ ebenfalls eine diskrete Zufallsgröße mit dem Symbolvorrat {0, 1, 2, ... , $I$}, die man als binomialverteilt bezeichnet. Der Symbolumfang beträgt somit $M = I + 1.$
Die Binomialverteilung findet in der Nachrichtentechnik ebenso wie in anderen Disziplinen mannigfaltige Anwendungen. Sie
- beschreibt die Verteilung von Ausschussstücken in der statistischen Qualitätskontrolle,
- erlaubt die Berechnung der Restfehlerwahrscheinlichkeit bei blockweiser Codierung.
Die per Simulation gewonnene Bitfehlerquote eines digitalen Übertragungssystems ist im Grunde genommen ebenfalls eine binomialverteilte Zufallsgröße.
Wahrscheinlichkeiten der Binomialverteilung
Für die Wahrscheinlichkeiten der Binomialverteilung gilt mit $μ = 0, ... , I:$ $$p_\mu = \rm Pr(\it z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$ Der erste Term gibt hierbei die Anzahl der Kombinationen („ $I$ über $μ$”) an: $${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{I\cdot (I- \rm 1)\cdot ...\cdot (\it I-\mu+ \rm 1)}{\rm 1\cdot \rm 2\cdot...\cdot \it \mu}.$$
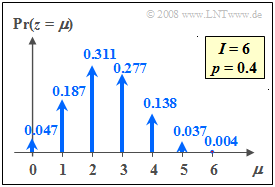 Die Grafik zeigt die Wahrscheinlichkeiten der Binomialverteilung sind für $I =$ 6 und $p =$ 0.4.
Die Grafik zeigt die Wahrscheinlichkeiten der Binomialverteilung sind für $I =$ 6 und $p =$ 0.4.
Für $I =$ 6 und $p =$ 0.5 ergeben sich die folgenden symmetrischen Binomialwahrscheinlichkeiten: $$\begin{align*}{\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}0) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}6)\hspace{-0.05cm} =\hspace{-0.05cm} 1/64\hspace{-0.05cm} = \hspace{-0.05cm}0.015625 ,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}1) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}5) \hspace{-0.05cm}= \hspace{-0.05cm}6/64 \hspace{-0.05cm}=\hspace{-0.05cm} 0.09375,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}2) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}4)\hspace{-0.05cm} = \hspace{-0.05cm}15/64 \hspace{-0.05cm}= \hspace{-0.05cm}0.234375 ,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}3) & = 20/64 \hspace{-0.05cm}= \hspace{-0.05cm} 0.3125 \hspace{0.05cm}.\end{align*}$$