Difference between revisions of "Theory of Stochastic Signals/Exponentially Distributed Random Variables"
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Kontinuierliche Zufallsgrößen |Vorherige Seite= Gaußverteilte Zufallsgröße |Nächste Seite=Weitere Verteilungen }} ==Einseitige Exp…“) |
|||
| Line 8: | Line 8: | ||
{{Definition}} | {{Definition}} | ||
Eine kontinuierliche Zufallsgröße $x$ nennt man (negativ-)exponentialverteilt, wenn sie nur nicht-negative Werte annehmen kann und die WDF für $x$ > 0 folgenden Verlauf hat: | Eine kontinuierliche Zufallsgröße $x$ nennt man (negativ-)exponentialverteilt, wenn sie nur nicht-negative Werte annehmen kann und die WDF für $x$ > 0 folgenden Verlauf hat: | ||
| − | $$ | + | $$f_x(x)=\it \lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$ |
| + | {{end}} | ||
| + | |||
| + | |||
| + | Das linke Bild zeigt die Wahrscheinlichkeitsdichtefunktion (WDF) einer exponentialverteilten Zufallsgröße $x$. Hervorzuheben ist: | ||
| + | *Definitionsgemäß gilt $f_{\rm x}(0) = λ/2.$ | ||
| + | *Je größer der Verteilungsparameter $λ$ ist, um so steiler erfolgt der Abfall. | ||
| + | |||
| + | |||
| + | [[File: P_ID72__Sto_T_3_6_S1_neu.png | WDF und VTF einer exponentialverteilten Zufallsgröße]] | ||
| + | |||
| + | Für die Verteilungsfunktion (rechtes Bild) erhält man für $r$ > 0 durch Integration über die WDF: | ||
| + | $$F_x(r)=1-\rm e^{\it -\lambda\hspace{0.05cm}\cdot \hspace{0.03cm} r}.$$ | ||
| + | |||
| + | Die Momente der Exponentialverteilung sind allgemein gleich $m_k = k!/λ^k.$ Daraus und aus dem Satz von Steiner ergibt sich für den Mittelwert und die Streuung: | ||
| + | $$m_1=\frac{1}{\lambda},$$ | ||
| + | $$\sigma=\sqrt{m_2-m_1^2}=\sqrt{\frac{2}{\lambda^2}-\frac{1}{\lambda^2}}=\frac{1}{\lambda}.$$ | ||
| + | |||
| + | {{Beispiel}} | ||
| + | Die Exponentialverteilung hat große Bedeutung für Zuverlässigkeitsuntersuchungen, wobei in diesem Zusammenhang auch der Begriff ''Lebensdauerverteilung'' üblich ist. Bei diesen Anwendungen ist die Zufallsgröße oft die Zeit $t$, die bis zum Ausfall einer Komponente vergeht. Desweiteren ist anzumerken, dass die Exponentialverteilung eng mit der Poissonverteilung in Zusammenhang steht. | ||
| + | {{end}} | ||
Revision as of 21:18, 29 May 2016
Einseitige Exponentialverteilung
Eine kontinuierliche Zufallsgröße $x$ nennt man (negativ-)exponentialverteilt, wenn sie nur nicht-negative Werte annehmen kann und die WDF für $x$ > 0 folgenden Verlauf hat: $$f_x(x)=\it \lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$
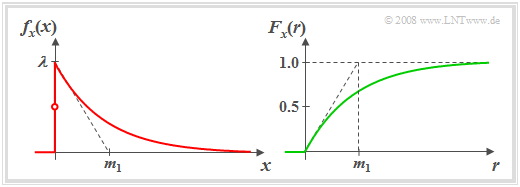
Das linke Bild zeigt die Wahrscheinlichkeitsdichtefunktion (WDF) einer exponentialverteilten Zufallsgröße $x$. Hervorzuheben ist:
- Definitionsgemäß gilt $f_{\rm x}(0) = λ/2.$
- Je größer der Verteilungsparameter $λ$ ist, um so steiler erfolgt der Abfall.
Für die Verteilungsfunktion (rechtes Bild) erhält man für $r$ > 0 durch Integration über die WDF: $$F_x(r)=1-\rm e^{\it -\lambda\hspace{0.05cm}\cdot \hspace{0.03cm} r}.$$
Die Momente der Exponentialverteilung sind allgemein gleich $m_k = k!/λ^k.$ Daraus und aus dem Satz von Steiner ergibt sich für den Mittelwert und die Streuung: $$m_1=\frac{1}{\lambda},$$ $$\sigma=\sqrt{m_2-m_1^2}=\sqrt{\frac{2}{\lambda^2}-\frac{1}{\lambda^2}}=\frac{1}{\lambda}.$$
Die Exponentialverteilung hat große Bedeutung für Zuverlässigkeitsuntersuchungen, wobei in diesem Zusammenhang auch der Begriff Lebensdauerverteilung üblich ist. Bei diesen Anwendungen ist die Zufallsgröße oft die Zeit $t$, die bis zum Ausfall einer Komponente vergeht. Desweiteren ist anzumerken, dass die Exponentialverteilung eng mit der Poissonverteilung in Zusammenhang steht.