Difference between revisions of "Theory of Stochastic Signals/Generalization to N-Dimensional Random Variables"
| Line 34: | Line 34: | ||
Die Matrix $\mathbf{K}$ zeigt bei reellen mittelwertfreien Gauß–Größen folgende weitere Eigenschaften: | Die Matrix $\mathbf{K}$ zeigt bei reellen mittelwertfreien Gauß–Größen folgende weitere Eigenschaften: | ||
| − | *Das Element der $i$-ten Zeile und $j$-ten Spalte lautet mit den beiden Streuungen $σ_i$ und $σ_j$ und dem Korrelationskoeffizienten $ρ_{ij}$. Formelmäßig gilt $K_{ij} = σ_i · σ_j · ρ_{ij} = K_{ji}.$ | + | *Das Element der $i$-ten Zeile und $j$-ten Spalte lautet mit den beiden Streuungen $σ_i$ und $σ_j$ und dem [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen#Korrelationskoeffizient|Korrelationskoeffizienten]] $ρ_{ij}$. Formelmäßig gilt $K_{ij} = σ_i · σ_j · ρ_{ij} = K_{ji}.$ |
*Berücksichtigt man noch die Beziehung $ρ_{ii} =$ 1, so erhält man für die Kovarianzmatrix: | *Berücksichtigt man noch die Beziehung $ρ_{ii} =$ 1, so erhält man für die Kovarianzmatrix: | ||
$${\mathbf{K}} =\left[ K_{ij} \right] = \left[ \begin{array}{cccc} | $${\mathbf{K}} =\left[ K_{ij} \right] = \left[ \begin{array}{cccc} | ||
| Line 88: | Line 88: | ||
{{Beispiel}} | {{Beispiel}} | ||
| − | Wir betrachten wie im Beispiel | + | Wir betrachten wie im Beispiel im letzten Abschnitt wieder eine 4D-Zufallsgröße $\mathbf{x}$, deren Kovarianzmatrix nur auf der Hauptdiagonalen besetzt ist: |
$${\mathbf{K}} = \left[ | $${\mathbf{K}} = \left[ | ||
\begin{array}{cccc} | \begin{array}{cccc} | ||
| Line 119: | Line 119: | ||
\hspace{0.1cm}+\hspace{0.1cm}\frac{x_2^2}{2\sigma_2^2}\hspace{0.1cm}+\hspace{0.1cm}\frac{x_3^2}{2\sigma_3^2}\hspace{0.1cm}+\hspace{0.1cm}\frac{x_4^2}{2\sigma_4^2}) | \hspace{0.1cm}+\hspace{0.1cm}\frac{x_2^2}{2\sigma_2^2}\hspace{0.1cm}+\hspace{0.1cm}\frac{x_3^2}{2\sigma_3^2}\hspace{0.1cm}+\hspace{0.1cm}\frac{x_4^2}{2\sigma_4^2}) | ||
\right]} .$$ | \right]} .$$ | ||
| − | Ein Vergleich mit Kapitel 4.2 zeigt, dass es sich um eine 4D-Zufallsgröße mit statistisch unabhängigen und unkorrelierten Komponenten handelt, da folgende Bedingung erfüllt ist: | + | Ein Vergleich mit [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen#Wahrscheinlichkeitsdichte-_und_Verteilungsfunktion_.281.29|Kapitel 4.2]] zeigt, dass es sich um eine 4D-Zufallsgröße mit statistisch unabhängigen und unkorrelierten Komponenten handelt, da folgende Bedingung erfüllt ist: |
$$\mathbf{f_x}(\mathbf{x})= \mathbf{f_{x1}}(\mathbf{x_1}) | $$\mathbf{f_x}(\mathbf{x})= \mathbf{f_{x1}}(\mathbf{x_1}) | ||
\cdot\mathbf{f_{x2}}(\mathbf{x_2}) | \cdot\mathbf{f_{x2}}(\mathbf{x_2}) | ||
| Line 125: | Line 125: | ||
\cdot\mathbf{f_{x4}}(\mathbf{x_4}) .$$ | \cdot\mathbf{f_{x4}}(\mathbf{x_4}) .$$ | ||
| − | Der Fall korrelierter Komponenten wird in Aufgaben zu diesem Kapitel eingehend behandelt. | + | Der Fall korrelierter Komponenten wird in [[Aufgaben:4.15_WDF_und_Korrelationsmatrix|Aufgaben zu diesem Kapitel]]eingehend behandelt. |
{{end}} | {{end}} | ||
Die folgenden Links verweisen auf Seiten mit Grundlagen der Matrizenrechnung am Kapitelende: | Die folgenden Links verweisen auf Seiten mit Grundlagen der Matrizenrechnung am Kapitelende: | ||
| + | |||
Determinante einer Matrix | Determinante einer Matrix | ||
| Line 206: | Line 207: | ||
Dagegen ist die Anzahl der möglichen Quantisierungswerte bei der gedrehten Zufallsgröße $\mathbf{ξ}$ um den Faktor 1.341 · 0.447 ≈ 0.6 geringer. Das bedeutet: Allein durch die Drehung des Koordinatensystems um 45° ⇒ ''Transformation der zweidimensionalen Zufallsgröße'' wurde eine Datenreduktion um 40% erreicht. | Dagegen ist die Anzahl der möglichen Quantisierungswerte bei der gedrehten Zufallsgröße $\mathbf{ξ}$ um den Faktor 1.341 · 0.447 ≈ 0.6 geringer. Das bedeutet: Allein durch die Drehung des Koordinatensystems um 45° ⇒ ''Transformation der zweidimensionalen Zufallsgröße'' wurde eine Datenreduktion um 40% erreicht. | ||
| − | Die Ausrichtung entsprechend den Hauptdiagonalen wurde für den zweidimensionalen Fall bereits auf der Seite Drehung des Koordinatensystems im Kapitel 4.2 behandelt, und zwar basierend auf geometrischen und trigonometrischen Überlegungen. Die Lösung des Problems mit Eigenwert und Eigenvektor ist äußerst elegant und zudem problemlos auf beliebig große Dimensionen $N$ erweiterbar. | + | Die Ausrichtung entsprechend den Hauptdiagonalen wurde für den zweidimensionalen Fall bereits auf der Seite [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen#Drehung_des_Koordinatensystems_.281.29|Drehung des Koordinatensystems]] im Kapitel 4.2 behandelt, und zwar basierend auf geometrischen und trigonometrischen Überlegungen. Die Lösung des Problems mit Eigenwert und Eigenvektor ist äußerst elegant und zudem problemlos auf beliebig große Dimensionen $N$ erweiterbar. |
{{end}} | {{end}} | ||
| Line 272: | Line 273: | ||
| − | Hierbei gibt $|\mathbf{A}| = a_{11} · a_{22} – a_{12} · a_{21}$ die Determinante an. Entsprechend gilt für $N =$ 3: | + | Hierbei gibt $|\mathbf{A}| = a_{11} · a_{22} – a_{12} · a_{21}$ die [[Stochastische_Signaltheorie/Verallgemeinerung_auf_N-dimensionale_Zufallsgrößen#Grundlagen_der_Matrizenrechnung:_Determinante_einer_Matrix|Determinante]] an. Entsprechend gilt für $N =$ 3: |
$$\left[ \begin{array}{ccc} | $$\left[ \begin{array}{ccc} | ||
b_{11} & b_{12} & b_{13}\\ | b_{11} & b_{12} & b_{13}\\ | ||
Revision as of 22:21, 26 January 2017
Contents
Korrelationsmatrix
Bisher wurden nur statistische Bindungen zwischen zwei (skalaren) Zufallsgrößen betrachtet. Für den allgemeineren Fall – einer Zufallsgröße mit $N$ Dimensionen – bietet sich zweckmäßigerweise eine Vektor- bzw. Matrixdarstellung an. Für die folgende Beschreibung wird vorausgesetzt:
- Die $N$–dimensionale Zufallsgröße wird als Vektor dargestellt:
$${\mathbf{x}} = [\hspace{0.03cm}x_1, \hspace{0.03cm}x_2, \hspace{0.1cm}... \hspace{0.1cm}, \hspace{0.03cm}x_N]^{\rm T}.$$
- Hierbei ist $\mathbf{x}$ ein Spaltenvektor, was aus dem Zusatz „T” – dies steht für „transponiert” – des angegebenen Zeilenvektors hervorgeht.
- Die $N$ Komponenten $x_i$ seien jeweils eindimensionale reelle Gaußsche Zufallsgrößen.
Statistische Bindungen zwischen den $N$ Zufallsgrößen werden durch die Korrelationsmatrix vollständig beschrieben:
$${\mathbf{R}} =\left[ R_{ij} \right] = \left[ \begin{array}{cccc}R_{11} & R_{12} & \cdots & R_{1N} \\ R_{21} & R_{22}& \cdots & R_{2N} \\ \cdots & \cdots & \cdots &\cdots \\ R_{N1} & R_{N2} & \cdots & R_{NN} \end{array} \right] .$$
Die $N^2$ Elemente dieser $N×N$-Matrix geben jeweils das gemeinsame Moment erster Ordnung zwischen zwei Komponenten an:
$$R_{ij}= {{\rm E}[x_i \cdot x_j ]} = R_{ji} .$$
In Vektorschreibweise lautet somit die Korrelationsmatrix:
$$\mathbf{R}= {\rm E[\mathbf{x} \cdot {\mathbf{x}}^{\rm T} ]} .$$
Da $\mathbf{x}$ ein Spaltenvektor mit $N$ Dimensionen ist und somit der transponierte Vektor $\mathbf{x}^{\rm T}$ ein Zeilenvektor gleicher Länge, ergibt das Produkt $\mathbf{x} · \mathbf{x}^{\rm T}$ eine $N×N$-Matrix. Dagegen wäre $\mathbf{x}^{\rm T}· \mathbf{x}$ eine 1×1-Matrix, also ein Skalar. Für den hier nicht weiter betrachteten Sonderfall komplexer Komponenten $x_i$ sind auch die Matrixelemente komplex:
$$R_{ij}= {{\rm E}[x_i \cdot x_j^{\star} ]} = R_{ji}^{\star} .$$
Die Realteile der Korrelationsmatrix sind weiterhin symmetrisch zur Hauptdiagonalen, während sich die dazugehörigen Imaginärteile durch das Vorzeichen unterscheiden.
Kovarianzmatrix
Man kommt von der Korrelationsmatrix $\mathbf{R}$ zur so genannten Kovarianzmatrix $${\mathbf{K}} =\left[ K_{ij} \right] = \left[ \begin{array}{cccc} K_{11} & K_{12} & \cdots & K_{1N} \\ K_{21} & K_{22}& \cdots & K_{2N} \\ \cdots & \cdots & \cdots & \cdots \\ K_{N1} & K_{N2} & \cdots & K_{NN} \end{array} \right] ,$$ wenn die Matrixelemente $K_{ij} = {\rm E}[(x_i – m_i) · (x_j – m_j)]$ jeweils ein Zentralmoment erster Ordnung angeben. Mit dem Vektor $\mathbf{m} = [m_1, m_2, ... , m_N]^{\rm T}$ kann somit auch geschrieben werden: $$\mathbf{K}= {{\rm E}[(\mathbf{x} - \mathbf{m}) (\mathbf{x} - \mathbf{m})^{\rm T} ]} .$$
Es soll ausdrücklich darauf hingewiesen werden, dass $m_1$ den Mittelwert der Komponente $x_1$ und $m_2$ den Mittelwert von $x_2$ bezeichnet – nicht etwa das Moment erster bzw. zweiter Ordnung.
Die Matrix $\mathbf{K}$ zeigt bei reellen mittelwertfreien Gauß–Größen folgende weitere Eigenschaften:
- Das Element der $i$-ten Zeile und $j$-ten Spalte lautet mit den beiden Streuungen $σ_i$ und $σ_j$ und dem Korrelationskoeffizienten $ρ_{ij}$. Formelmäßig gilt $K_{ij} = σ_i · σ_j · ρ_{ij} = K_{ji}.$
- Berücksichtigt man noch die Beziehung $ρ_{ii} =$ 1, so erhält man für die Kovarianzmatrix:
$${\mathbf{K}} =\left[ K_{ij} \right] = \left[ \begin{array}{cccc} \sigma_{1}^2 & \sigma_{1}\sigma_{2}\rho_{12} & \cdots & \sigma_{1}\sigma_{N}\rho_{1N} \\ \sigma_{2}\sigma_{1}\rho_{21} & \sigma_{2}^2& \cdots & \sigma_{2}\sigma_{N}\rho_{2N} \\ \cdots & \cdots & \cdots & \cdots \\ \sigma_{N}\sigma_{1}\rho_{N1} & \sigma_{N}\sigma_{2}\rho_{N2} & \cdots & \sigma_{N}^2 \end{array} \right] .$$
- Aufgrund der Beziehung $ρ_{ij} = ρ_{ji}$ ist die Kovarianzmatrix bei reellen Größen symmetrisch zur Hauptdiagonalen. Bei komplexen Größen würde dagegen $ρ_{ij} = ρ_{ji}^{\star}$ gelten.
Wir betrachten drei Kovarianzmatrizen: $${\mathbf{K}_2} = \left[ \begin{array}{cc} 1 & -0.5 \\ -0.5 & 1 \end{array} \right], \hspace{0.2cm}{\mathbf{K}_3} = 4 \cdot \left[ \begin{array}{ccc} 1 & 1/2 & 1/4\\ 1/2 & 1 & 3/4 \\ 1/4 & 3/4 & 1 \end{array}\right], \hspace{0.2cm}{\mathbf{K}_4} = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 9 & 0 \\ 0 & 0 & 0 & 16 \end{array} \right].$$
- $\mathbf{K}_2$ beschreibt eine 2D–Zufallsgröße, wobei der Korrelationskoeffizient $ρ$ zwischen den zwei Komponenten –0.5 beträgt und beide Komponenten die Streuung $σ =$ 1 aufweisen.
- Bei der 3D-Zufallsgröße gemäß $\mathbf{K}_3$ haben alle Komponenten die gleiche Streuung $σ =$ 2. Die stärksten Bindungen bestehen zwischen $x_2$ und $x_3$; wobei $ρ_{23} =$ 3/4 gilt.
- Die vier Komponenten der durch $\mathbf{K}_4$ gekennzeichneten Zufallsgröße sind unkorreliert, bei Gaußscher WDF auch statistisch unabhängig. Die Streuungen sind $σ_i = i$ für $i =$ 1, ... , 4.
Zusammenhang zwischen Kovarianzmatrix und WDF
Die Wahrscheinlichkeitsdichtefunktion einer $N$-dimensionalen Gaußschen Zufallsgröße $\mathbf{x}$ lautet: $$\mathbf{f_x}(\mathbf{x})= \frac{1}{\sqrt{(2 \pi)^N \cdot |\mathbf{K}|}}\cdot {\rm exp}{\left[-\frac{1}{2}\cdot(\mathbf{x} - \mathbf{m})^{\rm T}\cdot\mathbf{K}^{-1} \cdot(\mathbf{x} - \mathbf{m}) \right]} .$$
Hierbei bezeichnen:
- $\mathbf{x}$ den Spaltenvektor der betrachteten $N$-dimensionalen Zufallsgröße,
- $\mathbf{m}$ den Spaltenvektor der zugehörigen Mittelwerte,
- $|\mathbf{K}|$ die Determinante der $N×N$–Kovarianzmatrix $\mathbf{K}$ – eine skalare Größe,
- $\mathbf{K}^{−1}$ die Inverse von $\mathbf{K}$; diese ist ebenfalls eine $N×N$-Matrix.
Die Multiplikationen des Zeilenvektors $(\mathbf{x} – \mathbf{m})^{\rm T}$, der Matrix $\mathbf{K}^{–1}$ und des Spaltenvektors $(\mathbf{x} – \mathbf{m})$ ergibt im Argument der Exponentialfunktion erwartungsgemäß ein Skalar.
Wir betrachten wie im Beispiel im letzten Abschnitt wieder eine 4D-Zufallsgröße $\mathbf{x}$, deren Kovarianzmatrix nur auf der Hauptdiagonalen besetzt ist: $${\mathbf{K}} = \left[ \begin{array}{cccc} \sigma_{1}^2 & 0 & 0 & 0 \\ 0 & \sigma_{2}^2 & 0 & 0 \\ 0 & 0 & \sigma_{3}^2 & 0 \\ 0 & 0 & 0 & \sigma_{4}^2 \end{array} \right].$$ Deren Determinante ist $|\mathbf{K}| = σ_1^2 · σ_2^2 · σ_3^2 · σ_4^2$. Die inverse Kovarianzmatrix ergibt sich zu: $${\mathbf{K}}^{-1} \cdot {\mathbf{K}} = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\mathbf{K}}^{-1} = \left[ \begin{array}{cccc} \sigma_{1}^{-2} & 0 & 0 & 0 \\ 0 & \sigma_{2}^{-2} & 0 & 0 \\ 0 & 0 & \sigma_{3}^{-2} & 0 \\ 0 & 0 & 0 & \sigma_{4}^{-2} \end{array} \right].$$
Für mittelwertfreie Größen $(\mathbf{m = 0})$ lautet somit die WDF: $$\mathbf{f_{\rm x}}(\mathbf{x})= \frac{1}{{(2 \pi)^2 \cdot \sigma_1\cdot \sigma_2\cdot \sigma_3\cdot \sigma_4}}\cdot {\rm exp}{\left[-(\frac{x_1^2}{2\sigma_1^2} \hspace{0.1cm}+\hspace{0.1cm}\frac{x_2^2}{2\sigma_2^2}\hspace{0.1cm}+\hspace{0.1cm}\frac{x_3^2}{2\sigma_3^2}\hspace{0.1cm}+\hspace{0.1cm}\frac{x_4^2}{2\sigma_4^2}) \right]} .$$ Ein Vergleich mit Kapitel 4.2 zeigt, dass es sich um eine 4D-Zufallsgröße mit statistisch unabhängigen und unkorrelierten Komponenten handelt, da folgende Bedingung erfüllt ist: $$\mathbf{f_x}(\mathbf{x})= \mathbf{f_{x1}}(\mathbf{x_1}) \cdot\mathbf{f_{x2}}(\mathbf{x_2}) \cdot\mathbf{f_{x3}}(\mathbf{x_3}) \cdot\mathbf{f_{x4}}(\mathbf{x_4}) .$$
Der Fall korrelierter Komponenten wird in Aufgaben zu diesem Kapiteleingehend behandelt.
Die folgenden Links verweisen auf Seiten mit Grundlagen der Matrizenrechnung am Kapitelende:
Determinante einer Matrix
Inverse einer Matrix
Eigenwerte und Eigenvektoren (1)
Wir gehen weiter von einer $N×N$–Kovarianzmatrix $\mathbf{K}$ aus. Hieraus lassen sich die $N$ Eigenwerte – im Folgenden mit $λ_1 ... λ_N$ bezeichnet – wie folgt berechnen: $$|{\mathbf{K}} - \lambda \cdot {\mathbf{E}}| = 0.$$ $\mathbf{E}$ ist die Einheits-Diagonalmatrix der Dimension $N$.
Ausgehend von einer 2×2-Matrix $\mathbf{K}$ mit $K_{11} = K_{22} =$ 1 und $K_{12} = K_{21} =$ 0.8 erhält man als Bestimmungsgleichung: $${\rm det}\left[ \begin{array}{cc} 1- \lambda & 0.8 \\ 0.8 & 1- \lambda \end{array} \right] = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} (1- \lambda)^2 - 0.64 = 0.$$ Die beiden Eigenwerte sind somit $λ_1 =$ 1.8 und $λ_2 =$ 0.2.
Mit den so ermittelten Eigenwerten $λ_i (i = 1, ... , N)$ kann man die dazugehörigen Eigenvektoren $\boldsymbol{\xi_i}$ berechnen. Die $N$ vektoriellen Bestimmungsgleichungen lauten dabei:
$$({\mathbf{K}} - \lambda_i \cdot {\mathbf{E}}) \cdot
{\boldsymbol{\xi_i}} = 0\hspace{0.5cm}(i= 1, ... , N).$$
In Fortsetzung obiger Rechnung ergeben sich die beiden folgenden Eigenvektoren: $$\left[ \begin{array}{cc} 1- 1.8 & 0.8 \\ 0.8 & 1- 1.8 \end{array} \right]\cdot{\boldsymbol{\xi_1}} = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\boldsymbol{\xi_1}} = {\rm const.} \cdot\left[ \begin{array}{c} 1 \\ 1 \end{array} \right],$$ $$\left[ \begin{array}{cc} 1- 0.2 & 0.8 \\ 0.8 & 1- 0.2 \end{array} \right]\cdot{\boldsymbol{\xi_2}} = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\boldsymbol{\xi_2}} = {\rm const.} \cdot\left[ \begin{array}{c} -1 \\ 1 \end{array} \right].$$ Bringt man die Eigenvektoren in die so genannte Orthonormalfom (jeweils mit Betrag 1), so lauten sie: $${\boldsymbol{\xi_1}} = \frac{1}{\sqrt{2}} \cdot\left[ \begin{array}{c} 1 \\ 1 \end{array} \right], \hspace{0.5cm}{\boldsymbol{\xi_2}} = \frac{1}{\sqrt{2}} \cdot\left[ \begin{array}{c} -1 \\ 1 \end{array} \right].$$
Eigenwerte und Eigenvektoren (2)
Abschließend soll diskutiert werden, wie Eigenwert und Eigenvektor in der Informationstechnik genutzt werden können, beispielsweise zum Zwecke der Datenreduktion.
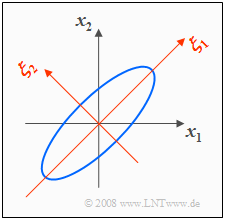 Wir gehen von den Parameterwerten des soeben betrachteten Beispiels aus.
Wir gehen von den Parameterwerten des soeben betrachteten Beispiels aus.
- Mit $σ_1 = σ_2 =$ 1 und $ρ =$ 0.8 ergibt sich die nachfolgend skizzierte 2D-WDF mit elliptischen Höhenlinien.
- Die Ellipsenhauptachse liegt hier wegen $σ_1 = σ_2$ unter einem Winkel von 45 Grad.
In der Grafik ist zusätzlich das $(ξ_1, ξ_2)$-Koordinatensystem eingezeichnet, das durch die Eigenvektoren $\mathbf{ξ}_1$ und $\mathbf{ξ}_2$ der Korrelationsmatrix aufgespannt wird. Die Eigenwerte $λ_1 =$ 1.8 und $λ_2 =$ 0.2 geben die Varianzen bezüglich des neuen Koordinatensystems an. Die Streuungen sind somit $σ_1 = \rm 1.8^{0.5}$ ≈ 1.341 und $σ_2 = \rm 0.2^{0.5}$ ≈ 0.447.
Soll eine 2D-Zufallsgröße $\mathbf{x}$ in seinen beiden Dimensionen $x_1$ und $x_2$ im Bereich zwischen $–5σ$ und $+5σ$ im Abstand $Δx =$ 0.01 quantisiert werden, so gibt es $\rm 10^6$ mögliche Quantisierungswerte $(σ_1 = σ_2 = σ =$ 1 vorausgesetzt).
Dagegen ist die Anzahl der möglichen Quantisierungswerte bei der gedrehten Zufallsgröße $\mathbf{ξ}$ um den Faktor 1.341 · 0.447 ≈ 0.6 geringer. Das bedeutet: Allein durch die Drehung des Koordinatensystems um 45° ⇒ Transformation der zweidimensionalen Zufallsgröße wurde eine Datenreduktion um 40% erreicht.
Die Ausrichtung entsprechend den Hauptdiagonalen wurde für den zweidimensionalen Fall bereits auf der Seite Drehung des Koordinatensystems im Kapitel 4.2 behandelt, und zwar basierend auf geometrischen und trigonometrischen Überlegungen. Die Lösung des Problems mit Eigenwert und Eigenvektor ist äußerst elegant und zudem problemlos auf beliebig große Dimensionen $N$ erweiterbar.
Grundlagen der Matrizenrechnung: Determinante einer Matrix
Wir betrachten die beiden quadratischen Matrizen mit Dimension $N =$ 2 bzw. $N =$ 3: $${\mathbf{A}} = \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right], \hspace{0.5cm}{\mathbf{B}} = \left[ \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{array}\right].$$
Die beiden Determinanten dieser Matrizen lauten: $$|{\mathbf{A}}| = a_{11} a\cdot a_{22} - a_{12} \cdot a_{21},$$ $$|{\mathbf{B}}| = b_{11} \cdot b_{22} \cdot b_{33} + b_{12} \cdot b_{23} \cdot b_{31} + b_{13} \cdot b_{21} \cdot b_{32} -$$ $$ - b_{11} \cdot b_{23} \cdot b_{32} - b_{12} \cdot b_{21} \cdot b_{33}- b_{13} \cdot b_{22} \cdot b_{31}.$$
Bitte beachten Sie:
- Die Determinante der Matrix $\mathbf{A}$ lässt sich geometrisch als die Fläche des durch die beiden Zeilenvektoren $(a_{11}, a_{12})$ und $(a_{21}, a_{22})$ aufgespannten Parallelogramms interpretieren.
- Die Fläche des durch die beiden Spaltenvektoren $(a_{11}, a_{21})^{\rm T}$ und $(a_{12}, a_{22})^{\rm T}$ festgelegten Parallelogramms ist ebenfalls $|\mathbf{A}|$.
- Dagegen ist die Determinante der Matrix $\mathbf{B}$ bei analoger geometrischer Interpretation als Volumen zu verstehen.
Für $N$ > 2 ist es möglich, sogenannte Unterdeterminanten zu bilden. Die Unterdeterminante einer $N×N$–Matrix bezüglich der Stelle $i, j$ ist die Determinante der $(N– {\rm 1})×(N–{\rm 1})$–Matrix, die sich ergibt, wenn man die $i$-te Zeile und die $j$-te Spalte streicht. Als Kofaktor bezeichnet man dann den Wert der Unterdeterminante gewichtet mit dem Vorzeichen $(–{\rm 1})^{i+j}$.
Ausgehend von der 3×3–Matrix $\mathbf{B}$ lauten die Kofaktoren der zweiten Zeile: $$B_{21} = -(b_{12} \cdot b_{23} - b_{13} \cdot b_{32})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j =3,$$ $$B_{22} = +(b_{11} \cdot b_{23} - b_{13} \cdot b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=4,$$ $$B_{23} = -(b_{11} \cdot b_{32} - b_{12} \cdot b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=5.$$
Die Determinante von $\mathbf{B}$ ergibt sich mit diesen Kofaktoren zu: $$|{\mathbf{B}}| = b_{21} \cdot B_{21} +b_{22} \cdot B_{22} +b_{23} \cdot B_{23}.$$ Die Determinante wurde hier nach der zweiten Zeile entwickelt. Entwickelt man $\mathbf{B}$ nach einer anderen Zeile oder Spalte, so ergibt sich für $|\mathbf{B}|$ der gleiche Zahlenwert.
Grundlagen der Matrizenrechnung: Inverse einer Matrix
Häufig benötigt man die Inverse $\mathbf{M}^{–1}$ der quadratischen Matrix $\mathbf{M}$. Die inverse Matrix $\mathbf{M}^{–1}$ besitzt die gleiche Dimension $N$ wie $\mathbf{M}$ und ist wie folgt definiert, wobei $\mathbf{E}$ die Einheitsmatrix (Diagonalmatrix) bezeichnet: $${\mathbf{M}}^{-1} \cdot {\mathbf{M}} ={\mathbf{E}} = \left[ \begin{array}{cccc} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & 1 \end{array} \right] .$$
Die Inverse der 2×2–Matrix $\mathbf{A}$ lautet demnach:
$$\left[ \begin{array}{cc}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array} \right]^{-1} = \frac{1}{|{\mathbf{A}}|} \hspace{0.1cm}\cdot \left[ \begin{array}{cc}
a_{22} & -a_{12} \\
-a_{21} & a_{11}
\end{array} \right].$$
Hierbei gibt $|\mathbf{A}| = a_{11} · a_{22} – a_{12} · a_{21}$ die Determinante an. Entsprechend gilt für $N =$ 3:
$$\left[ \begin{array}{ccc}
b_{11} & b_{12} & b_{13}\\
b_{21} & b_{22} & b_{23}\\
b_{31} & b_{32} & b_{33}
\end{array}\right]^{-1} = \frac{1}{|{\mathbf{B}}|} \hspace{0.1cm}\cdot\left[ \begin{array}{ccc}
B_{11} & B_{21} & B_{31}\\
B_{12} & B_{22} & B_{32}\\
B_{13} & B_{23} & B_{33}
\end{array}\right].$$
Die Determinante $|\mathbf{B}|$ einer 3×3–Matrix wurde auf der letzten Seite angegeben, ebenso wie die Vorschrift zur Berechnung der Kofaktoren $B_{ij}$. Diese beschreiben die Unterdeterminanten von $\mathbf{B}$, gewichtet mit den Positionsvorzeichen ${\rm (–1)}^{i+j}$. Zu beachten ist die Vertauschung der Zeilen und Spalten bei der Inversen.