Difference between revisions of "Theory of Stochastic Signals/Generalization to N-Dimensional Random Variables"
| Line 49: | Line 49: | ||
| − | The covariance matrix $\mathbf{K}$ shows the following further properties for real mean | + | The covariance matrix $\mathbf{K}$ shows the following further properties for real zero mean Gaussian variables: |
| − | *The element of $i$-th row and $j$-th column is with the two | + | *The element of $i$-th row and $j$-th column is with the two standard deviations $σ_i$ and $σ_j$ and the [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables#Correlation_coefficient|Correlation coefficient]] $ρ_{ij}$: |
:$$K_{ij} = σ_i ⋅ σ_j ⋅ ρ_{ij} = K_{ji}.$$ | :$$K_{ij} = σ_i ⋅ σ_j ⋅ ρ_{ij} = K_{ji}.$$ | ||
*Adding the relation $ρ_{ii} = 1$, we obtain for the covariance matrix: | *Adding the relation $ρ_{ii} = 1$, we obtain for the covariance matrix: | ||
| Line 80: | Line 80: | ||
* $\mathbf{K}_2$ describes a 2D random variable, where the correlation coefficient $ρ$ between the two components is $-0.5$ and both components have dispersion $σ = 1$ . | * $\mathbf{K}_2$ describes a 2D random variable, where the correlation coefficient $ρ$ between the two components is $-0.5$ and both components have dispersion $σ = 1$ . | ||
| − | *For the 3D random variable according to $\mathbf{K}_3$ all components have the same | + | *For the 3D random variable according to $\mathbf{K}_3$ all components have the same standard deviation $σ = 2$ (please note prefactor). The strongest bindings here are between $x_2$ and $x_3$, where $ρ_{23} = 3/4$ holds. |
*The four components of the random variable denoted by $\mathbf{K}_4$ are uncorrelated, with Gaussian WDF also statistically independent. The variances are $σ_i^2 = i^2$ for $i = 1$, ... , $4$ ⇒ variances $σ_i = i$. }} | *The four components of the random variable denoted by $\mathbf{K}_4$ are uncorrelated, with Gaussian WDF also statistically independent. The variances are $σ_i^2 = i^2$ for $i = 1$, ... , $4$ ⇒ variances $σ_i = i$. }} | ||
| Line 147: | Line 147: | ||
| − | == | + | ==Eigenvalues and eigenvectors== |
<br> | <br> | ||
| − | + | We further assume an $N×N$-covariance matrix $\mathbf{K}$ . | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ From the $N×N$-covariance matrix $\mathbf{K}$ the $N$ '''eigenvalues''' $λ_1$, ... , $λ_N$ can be calculated as follows: |
| − | :$$\vert {\mathbf{K} } - \lambda \cdot {\mathbf{E} }\vert | + | :$$\vert {\mathbf{K} } - \lambda \cdot {\mathbf{E} }\vert = 0.$$ |
| − | $\mathbf{E}$ | + | $\mathbf{E}$ is the unit diagonal matrix of dimension $N$.}} |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ Given a 2×2 matrix $\mathbf{K}$ with $K_{11} = K_{22} = 1$ and $K_{12} = K_{21} = 0.8$ we obtain as a determinant equation: |
:$${\rm det}\left[ \begin{array}{cc} | :$${\rm det}\left[ \begin{array}{cc} | ||
1- \lambda & 0.8 \\ | 1- \lambda & 0.8 \\ | ||
| Line 164: | Line 164: | ||
\end{array} \right] = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} | \end{array} \right] = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} | ||
(1- \lambda)^2 - 0.64 = 0.$$ | (1- \lambda)^2 - 0.64 = 0.$$ | ||
| − | + | Thus, the two eigenvalues are $λ_1 = 1.8$ and $λ_2 = 0.2$. }} | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Using the eigenvalues thus obtained $λ_i \ (i = 1$, ... , $N)$ one can compute the corresponding '''eigenvectors'''' $\boldsymbol{\xi_i}$ . |
| − | * | + | *The $N$ vectorial equations of determination are thereby: |
:$$({\mathbf{K} } - \lambda_i \cdot {\mathbf{E} }) \cdot | :$$({\mathbf{K} } - \lambda_i \cdot {\mathbf{E} }) \cdot | ||
{\boldsymbol{\xi_i} } = 0\hspace{0.5cm}(i= 1, \hspace{0.1cm}\text{...} \hspace{0.1cm} , N).$$}} | {\boldsymbol{\xi_i} } = 0\hspace{0.5cm}(i= 1, \hspace{0.1cm}\text{...} \hspace{0.1cm} , N).$$}} | ||
| − | {{GraueBox|TEXT= | + | {{GraueBox|TEXT= |
| − | $\text{ | + | $\text{Example 4:}$ Continuing the calculation in $\text{Example 3}$ yields the following two eigenvectors: |
:$$\left[ \begin{array}{cc} | :$$\left[ \begin{array}{cc} | ||
1- 1.8 & 0.8 \\ | 1- 1.8 & 0.8 \\ | ||
0.8 & 1- 1.8 | 0.8 & 1- 1.8 | ||
| − | \end{array} \right]\cdot{\boldsymbol{\xi_1} } = 0 \hspace{0.5cm}\ | + | \end{array} \right]\cdot{\boldsymbol{\xi_1} } = 0 \hspace{0.5cm}\rightarrow \hspace{0.5cm} |
{\boldsymbol{\xi_1} } = {\rm const.} \cdot\left[ \begin{array}{c} | {\boldsymbol{\xi_1} } = {\rm const.} \cdot\left[ \begin{array}{c} | ||
| − | +1 | + | +1 \\ |
+1 | +1 | ||
\end{array} \right],$$ | \end{array} \right],$$ | ||
| Line 187: | Line 187: | ||
1- 0.2 & 0.8 \\ | 1- 0.2 & 0.8 \\ | ||
0.8 & 1- 0.2 | 0.8 & 1- 0.2 | ||
| − | \end{array} \right]\cdot{\boldsymbol{\xi_2} } = 0 \hspace{0.5cm}\ | + | \end{array} \right]\cdot{\boldsymbol{\xi_2} } = 0 \hspace{0.5cm}\rightarrow \hspace{0.5cm} |
{\boldsymbol{\xi_2} } = {\rm const.} \cdot\left[ \begin{array}{c} | {\boldsymbol{\xi_2} } = {\rm const.} \cdot\left[ \begin{array}{c} | ||
| − | -1 | + | -1 \\ |
+1 | +1 | ||
\end{array} \right].$$ | \end{array} \right].$$ | ||
| − | + | Bringing the eigenvectors into the so-called orthonormal form $($each with magnitude $1)$, they are: | |
:$${\boldsymbol{\xi_1} } = \frac{1}{\sqrt{2} } \cdot\left[ \begin{array}{c} | :$${\boldsymbol{\xi_1} } = \frac{1}{\sqrt{2} } \cdot\left[ \begin{array}{c} | ||
| − | +1 | + | +1 \\ |
+1 | +1 | ||
\end{array} \right], \hspace{0.5cm}{\boldsymbol{\xi_2} } = \frac{1}{\sqrt{2} } \cdot\left[ \begin{array}{c} | \end{array} \right], \hspace{0.5cm}{\boldsymbol{\xi_2} } = \frac{1}{\sqrt{2} } \cdot\left[ \begin{array}{c} | ||
| − | -1 | + | -1 \\ |
+1 | +1 | ||
\end{array} \right].$$}} | \end{array} \right].$$}} | ||
| − | == | + | ==Use of eigenvalues in information technology== |
<br> | <br> | ||
| − | [[File:P_ID667__Sto_T_4_7_S4_ganz_neu.png |frame| | + | [[File:P_ID667__Sto_T_4_7_S4_ganz_neu.png |frame| For data compression using eigenvalue determination | right]] |
| − | + | Finally, we will discuss how eigenvalue and eigenvector can be used in information technology, for example for the purpose of data reduction. | |
| − | + | We assume the same parameter values as in $\text{Example 3}$ and $\text{Example 4}$ . | |
| − | * | + | *With $σ_1 = σ_2 = 1$ and $ρ = 0.8$ we get the 2D–PDF with elliptic contour lines sketched on the right. |
| − | * | + | *The ellipse major axis here is at an angle of $45^\circ$ because of $σ_1 = σ_2$ . |
| − | + | The graph also shows the $(ξ_1, ξ_2)$ coordinate system spanned by the eigenvectors $\mathbf{ξ}_1$ and $\mathbf{ξ}_2$ of the correlation matrix: | |
| − | * | + | *The eigenvalues $λ_1 = 1.8$ and $λ_2 = 0.2$ indicate the variances with respect to the new coordinate system. |
| − | * | + | *The variances are thus $σ_1 = \sqrt{1.8} ≈ 1.341$ and $σ_2 = \sqrt{0.2} ≈ 0.447$. |
<br clear=all> | <br clear=all> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 5:}$ Let a 2D random variable $\mathbf{x}$ in its two dimensions $x_1$ and $x_2$ in the range between $-5σ$ and $+5σ$ in distance $Δx = 0. 01$ to be quantized, there are $\rm 10^6$ possible quantization values $(σ_1 = σ_2 = σ = 1$ provided$)$. |
| − | * | + | *In contrast, the number of possible quantization values for the rotated random variable $\mathbf{ξ}$ is smaller by a factor $1.341 - 0.447 ≈ 0.6$ . |
| − | * | + | *This means: Just by rotating the coordinate system by $45^\circ$ ⇒ ''transforming the 2D–random variable'' the amount of data is reduced by about $40\%$ . |
| − | + | The alignment according to the main diagonals has already been treated for the two-dimensional case on the page [[Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables#Rotation_of_the_coordinate_system|Rotation of the Coordinate System]] , based on geometric and trigonometric considerations. | |
| − | + | The problem solution with eigenvalue and eigenvector is extremely elegant and can be easily extended to arbitrarily large dimensions $N$ .}} | |
==Basics of matrix operations: Determinant of a matrix== | ==Basics of matrix operations: Determinant of a matrix== | ||
<br> | <br> | ||
| − | + | We consider the two square matrices with dimension $N = 2$ resp. $N = 3$: | |
:$${\mathbf{A}} = \left[ \begin{array}{cc} | :$${\mathbf{A}} = \left[ \begin{array}{cc} | ||
a_{11} & a_{12} \\ | a_{11} & a_{12} \\ | ||
a_{21} & a_{22} | a_{21} & a_{22} | ||
\end{array} \right], | \end{array} \right], | ||
| − | \hspace{0.5cm}{\mathbf{B}} = | + | \hspace{0.5cm}{\mathbf{B}} = \left[ \begin{array}{ccc} |
b_{11} & b_{12} & b_{13}\\ | b_{11} & b_{12} & b_{13}\\ | ||
b_{21} & b_{22} & b_{23}\\ | b_{21} & b_{22} & b_{23}\\ | ||
| Line 238: | Line 238: | ||
\end{array}\right].$$ | \end{array}\right].$$ | ||
| − | + | The determinants of these two matrices are: | |
:$$|{\mathbf{A}}| = a_{11} \cdot a_{22} - a_{12} \cdot a_{21},$$ | :$$|{\mathbf{A}}| = a_{11} \cdot a_{22} - a_{12} \cdot a_{21},$$ | ||
| − | :$$|{\mathbf{B}}| | + | :$$|{\mathbf{B}}| = b_{11} \cdot b_{22} \cdot b_{33} + b_{12} \cdot |
| − | b_{23} \cdot b_{31} + b_{13} \cdot b_{21} \cdot b_{32} | + | b_{23} \cdot b_{31} + b_{13} \cdot b_{21} \cdot b_{32} - |
b_{11} \cdot b_{23} \cdot b_{32} - | b_{11} \cdot b_{23} \cdot b_{32} - | ||
b_{12} \cdot b_{21} \cdot b_{33}- | b_{12} \cdot b_{21} \cdot b_{33}- | ||
b_{13} \cdot b_{22} \cdot b_{31}.$$ | b_{13} \cdot b_{22} \cdot b_{31}.$$ | ||
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= |
| − | $\text{ | + | $\text{Please note:}$ |
| − | * | + | *The determinant of $\mathbf{A}$ corresponds geometrically to the area of the parallelogram spanned by the row vectors $(a_{11}, a_{12})$ and $(a_{21}, a_{22})$ . |
| − | * | + | *The area of the parallelogram defined by the two column vectors $(a_{11}, a_{21})^{\rm T}$ and $(a_{12}, a_{22})^{\rm T}$ is also $\vert \mathbf{A}\vert$. |
| − | * | + | *On the other hand, the determinant of the matrix $\mathbf{B}$ is to be understood as volume by analogous geometric interpretation}}. |
| − | + | For $N > 2$ it is possible to form so-called ''subdeterminants'' . | |
| − | * | + | *The subdeterminant of an $N×N$-matrix with respect to the place $(i, j)$ is the determinant of the $(N-1)×(N-1)$-matrix that results when the $i$-th row and the $j$-th column are deleted. |
| − | * | + | *The cofactor is then the value of the subdeterminant weighted by the sign $(-1)^{i+j}$. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 6:}$ Starting from the $3×3$ matrix $\mathbf{B}$ the cofactors of the second row are: |
| − | :$$B_{21} | + | :$$B_{21} = -(b_{12} \cdot b_{23} - b_{13} \cdot |
b_{32})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j =3,$$ | b_{32})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j =3,$$ | ||
| − | :$$B_{22} | + | :$$B_{22} = +(b_{11} \cdot b_{23} - b_{13} \cdot |
b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=4,$$ | b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=4,$$ | ||
| − | :$$B_{23} | + | :$$B_{23} = -(b_{11} \cdot b_{32} - b_{12} \cdot |
b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=5.$$ | b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=5.$$ | ||
| − | + | The determinant of $\mathbf{B}$ is obtained with these cofactors to: | |
| − | :$$\vert {\mathbf{B} } \vert | + | :$$\vert {\mathbf{B} } \vert = b_{21} \cdot B_{21} +b_{22} \cdot B_{22} |
+b_{23} \cdot B_{23}.$$ | +b_{23} \cdot B_{23}.$$ | ||
| − | * | + | *The determinant was developed here after the second line. |
| − | * | + | *Developing $\mathbf{B}$ according to another row or column, we get $\vert \mathbf{B} \vert$ of course the same numerical value.}} |
==Basics of matrix operations: Inverse of a matrix== | ==Basics of matrix operations: Inverse of a matrix== | ||
<br> | <br> | ||
| − | + | Often one needs the inverse $\mathbf{M}^{-1}$ of the square matrix $\mathbf{M}$. The inverse matrix $\mathbf{M}^{-1}$ has the same dimension $N$ as $\mathbf{M}$ and is defined as follows, where $\mathbf{E}$ denotes again the ''unit matrix'' (diagonal matrix): | |
| − | :$${\mathbf{M}}^{-1} \cdot {\mathbf{M}} ={\mathbf{E}} = | + | :$${\mathbf{M}}^{-1} \cdot {\mathbf{M}} ={\mathbf{E}} =. |
\left[ \begin{array}{cccc} 1 & 0 & \cdots & 0 \\ | \left[ \begin{array}{cccc} 1 & 0 & \cdots & 0 \\ | ||
| − | 0 & 1 & \cdots & 0 \ | + | 0 & 1 & \cdots & 0 \ \cdots & \cdots & \cdots \\ |
| − | 0 & 0 & \cdots & 1 | + | 0 & 0 & \cdots & 1 \end{array} \right] .$$ |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{example 7:}$ |
| − | + | Thus, the inverse of the $2×2$ matrix $\mathbf{A}$ is: | |
:$$\left[ \begin{array}{cc} | :$$\left[ \begin{array}{cc} | ||
a_{11} & a_{12} \\ | a_{11} & a_{12} \\ | ||
| Line 292: | Line 292: | ||
\end{array} \right].$$ | \end{array} \right].$$ | ||
| − | + | Here, there $\vert\mathbf{A}\vert = a_{11} - a_{22} - a_{12} - a_{21}$ the [[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables#Basics_of_matrix_operations:_Determinant_of_a_matrix|Determinant]] }} | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 8:}$ |
| − | + | Correspondingly, for the $3×3$-matrix $\mathbf{B}$: | |
:$$\left[ \begin{array}{ccc} | :$$\left[ \begin{array}{ccc} | ||
b_{11} & b_{12} & b_{13}\\ | b_{11} & b_{12} & b_{13}\\ | ||
| Line 303: | Line 303: | ||
b_{31} & b_{32} & b_{33} | b_{31} & b_{32} & b_{33} | ||
\end{array}\right]^{-1} = \frac{1}{\vert{\mathbf{B} }\vert} \hspace{0.1cm}\cdot\left[ \begin{array}{ccc} | \end{array}\right]^{-1} = \frac{1}{\vert{\mathbf{B} }\vert} \hspace{0.1cm}\cdot\left[ \begin{array}{ccc} | ||
| − | B_{11} & B_{21} & B_{31} | + | B_{11} & B_{21} & B_{31}\ |
B_{12} & B_{22} & B_{32}\\ | B_{12} & B_{22} & B_{32}\\ | ||
B_{13} & B_{23} & B_{33} | B_{13} & B_{23} & B_{33} | ||
\end{array}\right].$$ | \end{array}\right].$$ | ||
| − | * | + | *The determinant $\vert\mathbf{B}\vert$ of a $3×3$ matrix was given on the last page, as well as the calculation rule of the cofactors $B_{ij}$: |
| − | * | + | *These describe the subdeterminants of $\mathbf{B}$, weighted by the position signs $(-1)^{i+j}$. |
| − | * | + | *Note the swapping of rows and columns for the inverse}}. |
==Exercises on the chapter== | ==Exercises on the chapter== | ||
Revision as of 14:35, 14 March 2022
Contents
- 1 Correlation matrix
- 2 Covariance matrix
- 3 Relationship between covariance matrix and PDF
- 4 Eigenvalues and eigenvectors
- 5 Use of eigenvalues in information technology
- 6 Basics of matrix operations: Determinant of a matrix
- 7 Basics of matrix operations: Inverse of a matrix
- 8 Exercises on the chapter
Correlation matrix
So far, only statistical bindings between two (scalar) random variables have been considered For the more general case of a random variable with $N$ dimensions, a vector– or matrix representation is convenient.
For the following description it is assumed:
- The $N$-dimensional random variable is represented as a vector:
- $${\mathbf{x}} = \big[\hspace{0.03cm}x_1, \hspace{0.03cm}x_2, \hspace{0.1cm}\text{...} \hspace{0.1cm}, \hspace{0.03cm}x_N \big]^{\rm T}.$$
- Here $\mathbf{x}$ is a column vector, which can be seen from the addition $\rm T$ - this stands for "transposed" - of the specified row vector.
- Let $N$ components $x_i$ each be one-dimensional real Gaussian random variables.
$\text{definition:}$ Statistical bindings between the $N$ random variables are fully described by the correlation matrix :
- $${\mathbf{R} } =\big[ R_{ij} \big] = \left[ \begin{array}{cccc}R_{11} & R_{12} & \cdots & R_{1N} \ R_{21} & R_{22}& \cdots & R_{2N} \ \cdots & \cdots & \cdots \ R_{N1} & R_{N2} & \cdots & R_{NN} \end{array} \right] .$$
The $N^2$ elements of this $N×N$ matrix each indicate the first-order joint moment between two components:
- $$R_{ij}= { {\rm E}\big[x_i \cdot x_j \big] } = R_{ji} .$$
Thus, in vector notation, the correlation matrix is:
- $$\mathbf{R}= {\rm E\big[\mathbf{x} \cdot {\mathbf{x} }^{\rm T} \big] } .$$
Please note:
- $\mathbf{x}$ is a column vector with $N$ dimensions and the transposed vector $\mathbf{x}^{\rm T}$ a row vector of equal length ⇒ the product $\mathbf{x} ⋅ \mathbf{x}^{\rm T}$ gives a $N×N$–matrix.
- In contrast $\mathbf{x}^{\rm T}⋅ \mathbf{x}$ would be a $1×1$–matrix, i.e. a scalar.
- For the special case of complex components $x_i$ not considered further here, the matrix elements are also complex:
- $$R_{ij}= {{\rm E}\big[x_i \cdot x_j^{\star} \big]} = R_{ji}^{\star} .$$
- The real parts of the correlation matrix ${\mathbf{R} }$ are still symmetric about the main diagonal, while the imaginary parts differ by sign.
Covariance matrix
$\text{Definition:}$ One moves from the correlation matrix $\mathbf{R} =\left[ R_{ij} \right]$ to the so-called covariance matrix
- $${\mathbf{K} } =\big[ K_{ij} \big] = \left[ \begin{array}{cccc}K_{11} & K_{12} & \cdots & K_{1N} \ K_{21} & K_{22}& \cdots & K_{2N} \ \cdots & \cdots & \cdots \ K_{N1} & K_{N2} & \cdots & K_{NN} \end{array} \right] ,$$
if the matrix elements $K_{ij} = {\rm E}\big[(x_i - m_i) - (x_j - m_j)\big]$ each specify a first order central moment .
Thus, with the vector $\mathbf{m} = [m_1, m_2$, ... , $m_N]^{\rm T}$ can also be written:
- $$\mathbf{K}= { {\rm E}\big[(\mathbf{x} - \mathbf{m}) (\mathbf{x} - \mathbf{m})^{\rm T} \big] } .$$
It should be explicitly noted that $m_1$ denotes the mean value of the component $x_1$ and $m_2$ denotes the mean value of $x_2$ - not, for example, the first or second order moment.
The covariance matrix $\mathbf{K}$ shows the following further properties for real zero mean Gaussian variables:
- The element of $i$-th row and $j$-th column is with the two standard deviations $σ_i$ and $σ_j$ and the Correlation coefficient $ρ_{ij}$:
- $$K_{ij} = σ_i ⋅ σ_j ⋅ ρ_{ij} = K_{ji}.$$
- Adding the relation $ρ_{ii} = 1$, we obtain for the covariance matrix:
- $${\mathbf{K}} =\left[ K_{ij} \right] = \left[ \begin{array}{cccc} \sigma_{1}^2 & \sigma_{1}\cdot \sigma_{2}\cdot\rho_{12} & \cdots & \sigma_{1}\cdot \sigma_{N} \cdot \rho_{1N} \\ \sigma_{2} \cdot \sigma_{1} \cdot \rho_{21} & \sigma_{2}^2& \cdots & \sigma_{2} \cdot \sigma_{N} \cdot\rho_{2N} \cdot \cdots & \cdots & \cdots \sigma_{N} \cdot \sigma_{1} \cdot \rho_{N1} & \sigma_{N}\cdot \sigma_{2} \cdot\rho_{N2} & \cdots & \sigma_{N}^2 \end{array} \right] .$$
- Because of the relation $ρ_{ij} = ρ_{ji}$ the covariance matrix is always symmetric about the main diagonal for real quantities. For complex quantities, $ρ_{ij} = ρ_{ji}^{\star}$ would hold.
$\text{Example 1:}$ We consider the three covariance matrices:
- $${\mathbf{K}_2} = \left[ \begin{array}{cc} 1 & -0.5 \\ -0.5 & 1 \end{array} \right], \hspace{0.9cm}{\mathbf{K}_3} = 4 \cdot \left[ \begin{array}{ccc} 1 & 1/2 & 1/4\\ 1/2 & 1 & 3/4 \\ 1/4 & 3/4 & 1 \end{array}\right], \hspace{0.9cm}{\mathbf{K}_4} = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 9 & 0 \\ 0 & 0 & 0 & 16 \end{array} \right].$$
- $\mathbf{K}_2$ describes a 2D random variable, where the correlation coefficient $ρ$ between the two components is $-0.5$ and both components have dispersion $σ = 1$ .
- For the 3D random variable according to $\mathbf{K}_3$ all components have the same standard deviation $σ = 2$ (please note prefactor). The strongest bindings here are between $x_2$ and $x_3$, where $ρ_{23} = 3/4$ holds.
- The four components of the random variable denoted by $\mathbf{K}_4$ are uncorrelated, with Gaussian WDF also statistically independent. The variances are $σ_i^2 = i^2$ for $i = 1$, ... , $4$ ⇒ variances $σ_i = i$.
Relationship between covariance matrix and PDF
$\text{Definition:}$ The probability density function (PDF) of an $N$-dimensional Gaussian random variable $\mathbf{x}$ is:
- $$f_\mathbf{x}(\mathbf{x})= \frac{1}{\sqrt{(2 \pi)^N \cdot \vert\mathbf{K}\vert } }\hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-1/2\hspace{0.05cm}\cdot \hspace{0.05cm}(\mathbf{x} - \mathbf{m})^{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}\mathbf{K}^{-1} \hspace{0.05cm}\cdot \hspace{0.05cm}(\mathbf{x} - \mathbf{m}) } .$$
Here denote:
- $\mathbf{x}$ the column vector of the considered $N$–dimensional random variable,
- $\mathbf{m}$ the column vector of the associated mean values,
- $\mathbf{K}\vert$ the determinant of the $N×N$-covariance matrix $\mathbf{K}$ - a scalar quantity,
- $\mathbf{K}^{-1}$ the inverse of $\mathbf{K}$; this is also an $N×N$-matrix.
The multiplications of the row vector $(\mathbf{x} - \mathbf{m})^{\rm T}$, the inverse matrix $\mathbf{K}^{-1}$ and the column vector $(\mathbf{x} - \mathbf{m})$ yields a scalar in the argument of the exponential function.
$\text{Example 2:}$ We consider as in $\text{Example 1}$ again a 4D random variable $\mathbf{x}$ whose covariance matrix is occupied only on the main diagonal:
- $${\mathbf{K} } = \left[ \begin{array}{cccc} \sigma_{1}^2 & 0 & 0 & 0 \\ 0 & \sigma_{2}^2 & 0 & 0 \\ 0 & 0 & \sigma_{3}^2 & 0 \\ 0 & 0 & 0 & \sigma_{4}^2 \end{array} \right].$$
Their determinant is $\vert \mathbf{K}\vert = σ_1^2 - σ_2^2 - σ_3^2 - σ_4^2$. The inverse covariance matrix results to:
- $${\mathbf{K} }^{-1} \cdot {\mathbf{K } } = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] \hspace{0.5cm}\rightarrow \hspace{0.5cm} {\mathbf{K} }^{-1} = \left[ \begin{array}{cccc} \sigma_{1}^{-2} & 0 & 0 & 0 \\ 0 & \sigma_{2}^{-2} & 0 & 0 \\ 0 & 0 & \sigma_{3}^{-2} & 0 \\ 0 & 0 & 0 & \sigma_{4}^{-2} \end{array} \right].$$
Thus, for zero mean quantities $(\mathbf{m = 0})$ the PDF is:
- $$\mathbf{ f_{\rm x} }(\mathbf{x})= \frac{1}{ {(2 \pi)^2 \cdot \sigma_1\cdot \sigma_2\cdot \sigma_3\cdot \sigma_4} }\cdot {\rm e}^{-({x_1^2}/{2\sigma_1^2} \hspace{0.1cm}+\hspace{0.1cm}{x_2^2}/{2\sigma_2^2}\hspace{0.1cm}+\hspace{0.1cm}{x_3^2}/{2\sigma_3^2}\hspace{0.1cm}+\hspace{0.1cm}{x_4^2}/{2\sigma_4^2}) } .$$
A comparison with the chapter Probability density function and cumulative distribution function shows that it is a 4D random variable with statistically independent and uncorrelated components, since the following condition is satisfied:
- $$\mathbf{f_x}(\mathbf{x})= \mathbf{f_{x1 } }(\mathbf{x_1}) \cdot \mathbf{f_{x2} }(\mathbf{x_2}) \cdot \mathbf{f_{x3} }(\mathbf{x_3} ) \cdot \mathbf{f_{x4} }(\mathbf{x_4} ) .$$
The case of correlated components is discussed in detail in the exercises on the chapter
.
The following links refer to two pages at the end of the chapter with basics of matrix opeations:
Eigenvalues and eigenvectors
We further assume an $N×N$-covariance matrix $\mathbf{K}$ .
$\text{Definition:}$ From the $N×N$-covariance matrix $\mathbf{K}$ the $N$ eigenvalues $λ_1$, ... , $λ_N$ can be calculated as follows:
- $$\vert {\mathbf{K} } - \lambda \cdot {\mathbf{E} }\vert = 0.$$
$\mathbf{E}$ is the unit diagonal matrix of dimension $N$.
$\text{Example 3:}$ Given a 2×2 matrix $\mathbf{K}$ with $K_{11} = K_{22} = 1$ and $K_{12} = K_{21} = 0.8$ we obtain as a determinant equation:
- $${\rm det}\left[ \begin{array}{cc} 1- \lambda & 0.8 \\ 0.8 & 1- \lambda \end{array} \right] = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} (1- \lambda)^2 - 0.64 = 0.$$
Thus, the two eigenvalues are $λ_1 = 1.8$ and $λ_2 = 0.2$.
$\text{Definition:}$ Using the eigenvalues thus obtained $λ_i \ (i = 1$, ... , $N)$ one can compute the corresponding eigenvectors' $\boldsymbol{\xi_i}$ .
- The $N$ vectorial equations of determination are thereby:
- $$({\mathbf{K} } - \lambda_i \cdot {\mathbf{E} }) \cdot {\boldsymbol{\xi_i} } = 0\hspace{0.5cm}(i= 1, \hspace{0.1cm}\text{...} \hspace{0.1cm} , N).$$
$\text{Example 4:}$ Continuing the calculation in $\text{Example 3}$ yields the following two eigenvectors:
- $$\left[ \begin{array}{cc} 1- 1.8 & 0.8 \\ 0.8 & 1- 1.8 \end{array} \right]\cdot{\boldsymbol{\xi_1} } = 0 \hspace{0.5cm}\rightarrow \hspace{0.5cm} {\boldsymbol{\xi_1} } = {\rm const.} \cdot\left[ \begin{array}{c} +1 \\ +1 \end{array} \right],$$
- $$\left[ \begin{array}{cc} 1- 0.2 & 0.8 \\ 0.8 & 1- 0.2 \end{array} \right]\cdot{\boldsymbol{\xi_2} } = 0 \hspace{0.5cm}\rightarrow \hspace{0.5cm} {\boldsymbol{\xi_2} } = {\rm const.} \cdot\left[ \begin{array}{c} -1 \\ +1 \end{array} \right].$$
Bringing the eigenvectors into the so-called orthonormal form $($each with magnitude $1)$, they are:
- $${\boldsymbol{\xi_1} } = \frac{1}{\sqrt{2} } \cdot\left[ \begin{array}{c} +1 \\ +1 \end{array} \right], \hspace{0.5cm}{\boldsymbol{\xi_2} } = \frac{1}{\sqrt{2} } \cdot\left[ \begin{array}{c} -1 \\ +1 \end{array} \right].$$
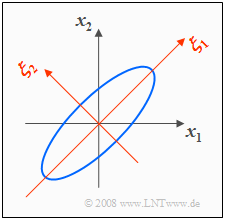
Use of eigenvalues in information technology
Finally, we will discuss how eigenvalue and eigenvector can be used in information technology, for example for the purpose of data reduction.
We assume the same parameter values as in $\text{Example 3}$ and $\text{Example 4}$ .
- With $σ_1 = σ_2 = 1$ and $ρ = 0.8$ we get the 2D–PDF with elliptic contour lines sketched on the right.
- The ellipse major axis here is at an angle of $45^\circ$ because of $σ_1 = σ_2$ .
The graph also shows the $(ξ_1, ξ_2)$ coordinate system spanned by the eigenvectors $\mathbf{ξ}_1$ and $\mathbf{ξ}_2$ of the correlation matrix:
- The eigenvalues $λ_1 = 1.8$ and $λ_2 = 0.2$ indicate the variances with respect to the new coordinate system.
- The variances are thus $σ_1 = \sqrt{1.8} ≈ 1.341$ and $σ_2 = \sqrt{0.2} ≈ 0.447$.
$\text{Example 5:}$ Let a 2D random variable $\mathbf{x}$ in its two dimensions $x_1$ and $x_2$ in the range between $-5σ$ and $+5σ$ in distance $Δx = 0. 01$ to be quantized, there are $\rm 10^6$ possible quantization values $(σ_1 = σ_2 = σ = 1$ provided$)$.
- In contrast, the number of possible quantization values for the rotated random variable $\mathbf{ξ}$ is smaller by a factor $1.341 - 0.447 ≈ 0.6$ .
- This means: Just by rotating the coordinate system by $45^\circ$ ⇒ transforming the 2D–random variable the amount of data is reduced by about $40\%$ .
The alignment according to the main diagonals has already been treated for the two-dimensional case on the page Rotation of the Coordinate System , based on geometric and trigonometric considerations.
The problem solution with eigenvalue and eigenvector is extremely elegant and can be easily extended to arbitrarily large dimensions $N$ .
Basics of matrix operations: Determinant of a matrix
We consider the two square matrices with dimension $N = 2$ resp. $N = 3$:
- $${\mathbf{A}} = \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right], \hspace{0.5cm}{\mathbf{B}} = \left[ \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{array}\right].$$
The determinants of these two matrices are:
- $$|{\mathbf{A}}| = a_{11} \cdot a_{22} - a_{12} \cdot a_{21},$$
- $$|{\mathbf{B}}| = b_{11} \cdot b_{22} \cdot b_{33} + b_{12} \cdot b_{23} \cdot b_{31} + b_{13} \cdot b_{21} \cdot b_{32} - b_{11} \cdot b_{23} \cdot b_{32} - b_{12} \cdot b_{21} \cdot b_{33}- b_{13} \cdot b_{22} \cdot b_{31}.$$
$\text{Please note:}$
- The determinant of $\mathbf{A}$ corresponds geometrically to the area of the parallelogram spanned by the row vectors $(a_{11}, a_{12})$ and $(a_{21}, a_{22})$ .
- The area of the parallelogram defined by the two column vectors $(a_{11}, a_{21})^{\rm T}$ and $(a_{12}, a_{22})^{\rm T}$ is also $\vert \mathbf{A}\vert$.
- On the other hand, the determinant of the matrix $\mathbf{B}$ is to be understood as volume by analogous geometric interpretation
.
For $N > 2$ it is possible to form so-called subdeterminants .
- The subdeterminant of an $N×N$-matrix with respect to the place $(i, j)$ is the determinant of the $(N-1)×(N-1)$-matrix that results when the $i$-th row and the $j$-th column are deleted.
- The cofactor is then the value of the subdeterminant weighted by the sign $(-1)^{i+j}$.
$\text{Example 6:}$ Starting from the $3×3$ matrix $\mathbf{B}$ the cofactors of the second row are:
- $$B_{21} = -(b_{12} \cdot b_{23} - b_{13} \cdot b_{32})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j =3,$$
- $$B_{22} = +(b_{11} \cdot b_{23} - b_{13} \cdot b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=4,$$
- $$B_{23} = -(b_{11} \cdot b_{32} - b_{12} \cdot b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=5.$$
The determinant of $\mathbf{B}$ is obtained with these cofactors to:
- $$\vert {\mathbf{B} } \vert = b_{21} \cdot B_{21} +b_{22} \cdot B_{22} +b_{23} \cdot B_{23}.$$
- The determinant was developed here after the second line.
- Developing $\mathbf{B}$ according to another row or column, we get $\vert \mathbf{B} \vert$ of course the same numerical value.
Basics of matrix operations: Inverse of a matrix
Often one needs the inverse $\mathbf{M}^{-1}$ of the square matrix $\mathbf{M}$. The inverse matrix $\mathbf{M}^{-1}$ has the same dimension $N$ as $\mathbf{M}$ and is defined as follows, where $\mathbf{E}$ denotes again the unit matrix (diagonal matrix):
- $${\mathbf{M}}^{-1} \cdot {\mathbf{M}} ={\mathbf{E}} =. \left[ \begin{array}{cccc} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \ \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & 1 \end{array} \right] .$$
$\text{example 7:}$ Thus, the inverse of the $2×2$ matrix $\mathbf{A}$ is:
- $$\left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]^{-1} = \frac{1}{\vert{\mathbf{A} }\vert} \hspace{0.1cm}\cdot \left[ \begin{array}{cc} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{array} \right].$$
Here, there $\vert\mathbf{A}\vert = a_{11} - a_{22} - a_{12} - a_{21}$ the Determinant
$\text{Example 8:}$ Correspondingly, for the $3×3$-matrix $\mathbf{B}$:
- $$\left[ \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{array}\right]^{-1} = \frac{1}{\vert{\mathbf{B} }\vert} \hspace{0.1cm}\cdot\left[ \begin{array}{ccc} B_{11} & B_{21} & B_{31}\ B_{12} & B_{22} & B_{32}\\ B_{13} & B_{23} & B_{33} \end{array}\right].$$
- The determinant $\vert\mathbf{B}\vert$ of a $3×3$ matrix was given on the last page, as well as the calculation rule of the cofactors $B_{ij}$:
- These describe the subdeterminants of $\mathbf{B}$, weighted by the position signs $(-1)^{i+j}$.
- Note the swapping of rows and columns for the inverse
.
Exercises on the chapter
Aufgabe 4.15: WDF und Korrelationsmatrix
Aufgabe 4.15Z: Aussagen der Kovarianzmatrix
Aufgabe 4.16: Eigenwerte und Eigenvektoren
Aufgabe 4.16Z: 2D- und 3D-Datenreduktion