Generation of Discrete Random Variables

Pseudorandom variables

One way to generate a binary random sequence $〈z_{\rm ν}〉 ∈ \{0, 1\}$ with good statistical properties is offered by the so-called pseudorandom generators, also known as PN generators, where "PN" stands for pseudonoise .

These have the following properties:

The binary sequence generated by such a generator is not stochastic in a strict sense, but exhibits periodic and thus deterministic properties.
If the period length $P$ is sufficiently large, the sequence appears to an observer as random with sufficiently good statistical properties for many applications.
The advantage of a pseudorandom generator over a "real" stochastic source is that the random sequence is reproducible if a few parameters are known.

$\text{Example 1:}$ The latter property also gives rise to the main applications of pseudo-noise generators:

first, the error frequency measurement in digital signal transmission,
secondly, for band spreading in CDMA (Code Division Multiple Access).

In such a Spread Spectrum System the transmit signal is modulated with a binary random sequence, whose symbol repetition frequency is significantly higher than the bit frequency. This offers the possibility of multiple channel utilization. Since the same sequence must be added in phase at the receiver, the use of reproducible PN sequences is also common here.

Detailed information on bandspreading methods can be found in the chapter UMTS - Universal Mobile Telecommunications System of the German book "Beispiele von Nachrichtensystemen" .

Realization of PN generators

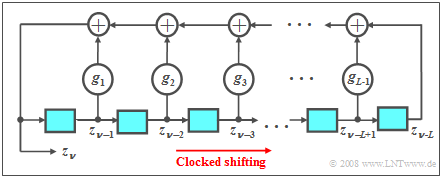
Pseudorandom generators are usually realized by feedback shift registers, where at each clock instant the content of the register is shifted one place to the right (see diagram). For the currently generated symbol, with $g_l ∈ \{0, 1\}$ and $l = 1$, ... , $L-1$:

$$z_\nu = (g_1\cdot z_{\nu-1}+g_2\cdot z_{\nu-2}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_l\cdot z_{\nu-l}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_{L-1}\cdot z_{\nu-L+1}+ z_{\nu-L})\hspace{0.1cm} \rm mod \hspace{0.2cm}2.$$

The binary values $z_{ν-1}$ to $z_{ν-L}$ generated at previous time points are stored in the memory cells of the shift register.
The coefficients $g_1$, ... , $g_{L-1}$ are also binary values, where a $1$ indicates a feedback at the corresponding location and a $0$ indicates no feedback.
Modulo-2 addition can be implemented, for example, using an XOR operation:

pseudo-noise generator

$$(x + y)\hspace{0.1cm} \rm mod\hspace{0.1cm}2 = \it x\hspace{0.1cm}\rm XOR\hspace{0.1cm} \it y = \left\{\begin{array}{*{2}{c}} \rm 0 & \rm falls\hspace{0.1cm} \it x= y,\rm 1 & \rm falls\hspace{0.1cm} \it x\neq y. \end{array} \right.$$

The statistical properties of the generated pseudonoise random sequence $〈z_{\rm ν}〉$ are essentially determined by.

the degree $L$, and
the feedback coefficients $g_{\hspace{0.05cm}l}$ $($with $l = 1$, ... , $L-1)$.

A prerequisite for the generation of a PN sequence is that not all memory elements are preallocated with zeros, otherwise the modulo-2 addition would always generate only the symbol $0$ .

To identify different PN generators one uses in the literature alternatively:

the so-called generator polynomials of the type.

$$G(D) = g_L\cdot D^L+g_{L-1}\cdot D^{L-1}+ \ \text{...} \ +g_1\cdot D+g_0 .$$

Here, always $g_0 = g_L = 1$ to be set and $D$ a formal parameter indicating a delay by one bar $(D^L$ indicates a delay by $L$ bars$)$;

the octal representation of the binary number $(g_L\ \text{ ...} \ g_2 \ g_1 \ g_0)$. It is important that here the feedback coefficients - starting from the right with $g_0$ - are combined into triples and these are written octal $(0 \ \text{...}\ 7)$.

$\text{Example 2:}$ The generator polynomial $D^4 + D^3 + 1$ belongs to a shift register of degree $L = 4$ with the following octal representation.

$$(g_4 \ g_3 \ g_2 \ g_1 \ g_0) = (11001)_{\rm bin} = (31)_{\rm oct}. $$

Folgen maximaler Länge (M-Sequenzen)

Sind nicht alle $L$ Speicherzellen des Schieberegisters mit Nullen vorbelegt, so entsteht stets eine periodische Zufallsfolge $〈z_ν\rangle$:

Die Periodenlänge $P$ dieser Folge hängt im starken Maße von den Rückkopplungskoeffizienten ab.
Für jeden Grad $L$ gibt es zumindest eine Konfiguration mit der maximalen Periodenlänge

$$P_{\rm max} = \rm 2^{\it L}-\rm 1.$$

Eine solche PN-Folge bezeichnet man auch oft als $\rm M-Sequenz$, wobei das $\rm M$ für „Maximal“ steht.

$\text{Vorerst ohne Beweis:}$

Eine $\rm M-Sequenz$ kann man daran erkennen, dass das Generatorpolynom $G(D)$ primitiv ist.
Wie im Buch Channel Coding ausführlich dargelegt wird, bezeichnet man ein Polynom $G(D)$ vom Grad $L$ als primitiv, wenn folgende Bedingung erfüllt ist:

$$\frac{(D^n+\rm 1)}{\it G(D)} \neq 0\hspace{0.5cm} {\rm f\ddot{u}r}\hspace{0.5cm}\it n<P_{\rm max} \rm = \rm 2^{\it L}-\rm 1.$$

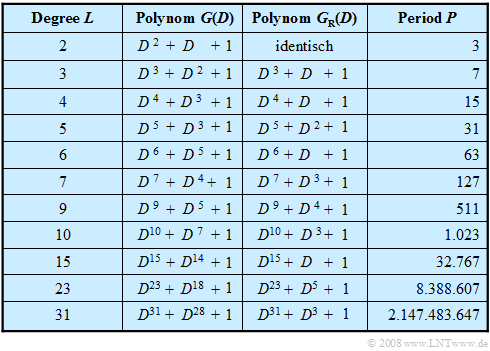
Zusammenstellung einiger günstiger Generatorpolynome

In der Tabelle sind PN-Generatoren maximaler Länge bis zum Grad $L = 31$ aufgeführt.

Die Auswahl ist auf Konfigurationen mit nur einer Anzapfung – also mit zwei Rückführungen – beschränkt.
Das bedeutet, dass die zugehörigen Polynome nur aus drei Summanden bestehen.
Für Applikationen, die eine hohe Geschwindigkeit erfordern, sind solche Generatoren sehr nützlich.

$\text{Beispiel 3:}$ Ein Schieberegister vom Grad $L = 4$ mit Oktalkennung $(31)$ und Generatorpolynom $G(D) = D^4 + D^3 + 1$ führt zu einer Folge maximaler Länge:

$$P_{\rm max} = 2^4 - 1 = 15.$$

Der mathematische Nachweis hierfür ist aufwändig:

Man muss anhand obiger Polynomdivision für $n = 1$, ... , $14$ zeigen, dass der Quotient stets ungleich Null ist.
Erst die Division $(D^{15} + 1)/G(D)$ darf ein Ergebnis ohne Rest liefern.
Hierbei ist zu berücksichtigen, dass in der Modulo-2-Algebra $+1$ und $–1$ identisch sind.

Reziproke Polynome

$\text{Definition:}$ Das zum Generatorpolynom $G(D)$ gehörige reziproke Polynom lautet:

$$G_{\rm R}(D)=D^{L}\cdot G(D^{-1}).$$

Zwischen den beiden Schiebregistern mit den Polynomen $G(D)$ bzw. $G_{\rm R}(D)$ bestehen folgende Zusammenhänge:

Liefert $G(D)$ eine Folge maximaler Länge ⇒ $P_{\rm max} = 2^L - 1$, so ist auch die Periodenlänge des reziproken Polynoms $G_{\rm R}(D)$ maximal.
Die Ausgangsfolgen reziproker Konfigurationen sind zueinander invers. Das heißt:
Die Folge von $G(D)$ – von rechts nach links gelesen – ergibt die Folge der reziproken Anordnung $G_{\rm R}(D)$.

In obiger Tabelle sind in der dritten Spalte die zu $G(D)$ zugehörigen reziproken Polynome $G_{\rm R}(D)$ bis zum Registergrad $L = 31$ angegeben.

$\text{Beispiel 4:}$ Wir betrachten wieder den Grad $L = 4$.

Ausgehend von der Schieberegisterstruktur $(31)_{\rm oct}$ erhält man für das reziproke Polynom

$$G_{\rm R}(D) = D^{\rm 4}\cdot (1+D^{-3} + D^{ -4})=D^{ 4}+D^{1}+\rm 1$$

und damit die Konfiguration mit der Oktalkennung $(23)$.

Die entsprechenden Ausgangsfolgen haben jeweils die maximale Periodenlänge $P_{\rm max} = 15$ und sind zueinander invers:
- ... $0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1$ ...
- ... $0 \ 1 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 1 \ 1 \ 1 \ 1$ ...

Das bedeutet, dass die obere Ausgangsfolge von $(31)$, von rechts nach links gelesen, die unten angegebene Folge der reziproken Anordnung $(23)$ ergibt.
Zu erkennen ist allerdings eine zyklische Phasenverschiebung um vier Binärstellen.

Die in diesem Abschnitt behandelte Thematik ist im Lernvideo Erläuterung der PN-Generatoren an einem Beispiel zusammengefasst.

Erzeugung mehrstufiger Zufallsgrößen

Viele höhere Programmiersprachen bieten Pseudo-Zufallsgeneratoren an, die reelle, zwischen $0$ und $1$ gleichverteilte Zufallszahlen $x$ liefern. Beispielsweise lautet ein entsprechender C-Funktionsaufruf:

$$x = \text{random()}.$$

Durch sukzessives Aufrufen der "Random-Funktion" entsteht eine periodisch sich wiederholende Folge reeller Zahlen, wobei alle Funktionswerte $0 \le x < 1$ gleichwahrscheinlich sind ⇒ siehe Kapitel Gleichverteilte Zufallsgrößen.

Da die Periodendauer $P$ jedoch sehr groß ist, kann diese Folge als pseudozufällig angesehen werden.
Durch Angabe eines Startwertes wird an bestimmten Stellen der Pseudozufallsfolge begonnen.

Bei der Generierung einer wertdiskreten mehrstufigen Zufallsgröße $z$ wird zweckmäßigerweise von einer solchen gleichverteilten Zufallsgröße $x$ ausgegangen.

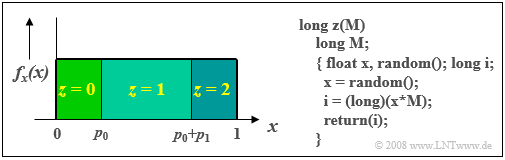
$\text{Beispiel 5:}$ Die Grafik zeigt das Prinzip für den Sonderfall $M = 3$, wobei die gewünschten Auftrittswahrscheinlichkeiten mit $p_0$, $p_1$ und $p_2$ bezeichnet sind.

Zur Erzeugung mehrstufiger Zufallsgrößen

Dann gilt:

Ist der aktuelle Wert $x$ der zwischen $0$ und $1$ gleichverteilten Zufallsgröße kleiner als $p_0$, so wird die ternäre Zufallsgröße $z = 0$ gesetzt.
Im Bereich $p_0 ≤ x < p_0 + p_1$ wird $z = 1$ ausgegeben.
Für $x \ge p_0 + p_1$ wird die Zufallsgröße zu $z =2$.

Im aufgeführten C-Programm ergibt sich für $M = 3$ und für den aktuellen Zufallswert $x = 0.57$ für das Produkt $x · M = 0.57 · 3 = 1.71$ und somit die diskrete Zufallsgröße $z = 1$. Für einen zweiten Zufallswert $x = 0.95$ würde die Funktion dagegen das Ergebnis $z = 2$ liefern.

Aus Verständnisgründen wurde hier eine umständliche Programmierung gewählt. Der angegebene C-Programmteil könnte auch kompakter geschrieben werden:

$$\text{\{ float random(); return((long) (random()*M)); \} }$$