Difference between revisions of "Theory of Stochastic Signals/Moments of a Discrete Random Variable"
| (39 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Discrete Random Variables |
| − | |Vorherige Seite= | + | |Vorherige Seite=From Random Experiment to Random Variable |
| − | |Nächste Seite= | + | |Nächste Seite=Binomial Distribution |
}} | }} | ||
| − | == | + | ==Calculation as ensemble average or time average== |
| − | + | <br> | |
| + | The probabilities and the relative frequencies provide extensive information about a discrete random variable. Reduced information is obtained by the so-called »'''moments'''« $m_k$, where $k$ represents a natural number. | ||
| − | + | {{BlueBox|TEXT= | |
| − | + | $\text{Two alternative ways of calculation:}$ | |
| − | |||
| − | |||
| − | |||
| + | Under the condition [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Ergodic_random_processes|»$\text{ergodicity}$«]] implicitly assumed here, there are two different calculation possibilities for the $k$-th order moment: | ||
| + | |||
| + | $\rm (A)$ the »'''ensemble averaging'''« or »expected value formation« ⇒ averaging over all possible values $\{ z_\mu\}$ with index $\mu = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , M$: | ||
| + | :$$m_k = {\rm E} \big[z^k \big] = \sum_{\mu = 1}^{M}p_\mu \cdot z_\mu^k \hspace{2cm} \rm with \hspace{0.1cm} {\rm E\big[\text{ ...} \big]\hspace{-0.1cm}:} \hspace{0.3cm} \rm expected\hspace{0.1cm}value ;$$ | ||
| + | $\rm (B)$ the »'''time averaging'''« over the random sequence $\langle z_ν\rangle$ with index $ν = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , N$: | ||
| + | :$$m_k=\overline{z_\nu^k}=\hspace{0.01cm}\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=\rm 1}^{\it N}z_\nu^k\hspace{1.7cm}\rm with\hspace{0.1cm}horizontal\hspace{0.1cm}line\hspace{-0.1cm}:\hspace{0.1cm}time\hspace{0.1cm}average.$$}} | ||
| − | |||
| − | + | <u>Note:</u> | |
| − | + | #Both types of calculations lead to the same asymptotic result for sufficiently large values of $N$. | |
| − | $ | + | #For finite $N$, a comparable error results as when the probability is approximated by the relative frequency. |
| − | |||
| − | {{ | + | ==First order moment – linear mean – DC component== |
| − | + | <br> | |
| − | $$m_1 = | + | {{BlueBox|TEXT= |
| − | + | $\text{Definition:}$ With $k = 1$ we obtain from the general equation the first order moment ⇒ the »'''linear mean'''«: | |
| + | :$$m_1 =\sum_{\mu=1}^{M}p_\mu\cdot z_\mu =\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=1}^{N}z_\nu.$$ | ||
| + | *The left part of this equation describes the ensemble averaging $($over all possible values$)$. | ||
| + | |||
| + | * The right equation gives the determination as time average. | ||
| + | |||
| + | *In the context of signals, this quantity is also referred to as the [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal|»$\text{direct current}$«]] $\rm (DC)$ component.}} | ||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | $ | + | [[File:P_ID49__Sto_T_2_2_S2_neu.png|right|frame|DC component $m_1$ of a binary signal]] |
| − | + | $\text{Example 1:}$ A binary signal $x(t)$ with the two possible values | |
| − | + | *$1\hspace{0.03cm}\rm V$ $($for symbol $\rm L)$, | |
| + | *$3\hspace{0.03cm}\rm V$ $($for symbol $\rm H)$ | ||
| − | |||
| − | |||
| − | |||
| − | + | as well as the occurrence probabilities $p_{\rm L} = 0.2$ and $p_{\rm H} = 0.8$ has the linear mean $($»DC component«$)$ | |
| − | $$\ | + | :$$m_1 = 0.2 \cdot 1\,{\rm V}+ 0.8 \cdot 3\,{\rm V}= 2.6 \,{\rm V}. $$ |
| − | + | This is drawn as a red line in the graph. | |
| − | + | If we determine this parameter by time averaging over the displayed $N = 12$ signal values, we obtain a slightly smaller value: | |
| + | :$$m_1\hspace{0.01cm}' = 4/12 \cdot 1\,{\rm V}+ 8/12 \cdot 3\,{\rm V}= 2.33 \,{\rm V}. $$ | ||
| + | #Here, the probabilities $p_{\rm L} = 0.2$ and $p_{\rm H} = 0.8$ were replaced by the corresponding frequencies $h_{\rm L} = 4/12$ and $h_{\rm H} = 8/12$ respectively. | ||
| + | #In this example the relative error due to insufficient sequence length $N$ is greater than $10\%$. | ||
| − | |||
| − | |||
| + | $\text{Note about our (admittedly somewhat unusual) nomenclature:}$ | ||
| − | + | We denote binary symbols here as in circuit theory with $\rm L$ $($Low$)$ and $\rm H$ $($High$)$ to avoid confusion. | |
| − | + | *In coding theory, it is useful to map $\{ \text{L, H}\}$ to $\{0, 1\}$ to take advantage of the possibilities of modulo algebra. | |
| − | '' | + | *In contrast, to describe modulation with bipolar $($antipodal$)$ signals, one better chooses the mapping $\{ \text{L, H}\}$ ⇔ $ \{-1, +1\}$. |
| − | $$ | + | }} |
| − | + | ||
| − | + | ||
| + | ==Second order moment – power – variance – standard deviation == | ||
| + | <br> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definitions:}$ | ||
| + | |||
| + | $\rm (A)$ Analogous to the linear mean, $k = 2$ obtains the »'''second order moment'''«: | ||
| + | :$$m_2 =\sum_{\mu=\rm 1}^{\it M}p_\mu\cdot z_\mu^2 =\lim_{N\to\infty}\frac{\rm 1}{\it N}\sum_{\nu=\rm 1}^{\it N}z_\nu^2.$$ | ||
| + | |||
| + | $\rm (B)$ Together with the DC component $m_1$ the »'''variance'''« $σ^2$ can be determined from this as a further parameter $($»Steiner's theorem«$)$: | ||
| + | :$$\sigma^2=m_2-m_1^2.$$ | ||
| + | $\rm (C)$ The »'''standard deviation'''« $σ$ is the square root of the variance: | ||
| + | :$$\sigma=\sqrt{m_2-m_1^2}.$$}} | ||
| + | |||
| + | |||
| + | $\text{Notes on units:}$ | ||
| + | |||
| + | #For a random signal $x(t)$ ⇒ the second moment $m_2$ gives the total power $($DC power plus AC power$)$ related to the resistance $1 \hspace{0.03cm} Ω$. | ||
| + | #If $x(t)$ describes a voltage, accordingly $m_2$ has the unit ${\rm V}^2$ and the rms value $($»root mean square«$)$ $x_{\rm eff}=\sqrt{m_2}$ has the unit ${\rm V}$. | ||
| + | #The total power for any reference resistance $R$ is calculated to $P=m_2/R$ and accordingly has the unit $\rm V^2/(V/A) = W$. | ||
| + | #If $x(t)$ describes a current waveform, then $m_2$ has the unit ${\rm A}^2$ and the rms value $x_{\rm eff}=\sqrt{m_2}$ has the unit ${\rm A}$. | ||
| + | #The total power for any reference resistance $R$ is calculated to $P=m_2\cdot R$ and accordingly has the unit $\rm A^2 \cdot(V/A) = W$. | ||
| + | #Only in the special case $m_1=0$ ⇒ the variance is $σ^2=m_2$. Then the standard deviation $σ$ coincides also with the rms value $x_{\rm eff}$ . | ||
| + | |||
| + | |||
| + | ⇒ The following $($German language$)$ learning video illustrates the defined quantities using the example of a digital signal: <br> [[Momentenberechnung bei diskreten Zufallsgrößen (Lernvideo)|»Momentenberechnung bei diskreten Zufallsgrößen»]] ⇒ »Moment Calculation for Discrete Random Variables». | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | [[File:P_ID456__Sto_T_2_2_S3_neu.png | right|frame|"Standard deviation" of a binary signal]] | ||
| + | |||
| + | $\text{Example 2:}$ | ||
| + | For a binary signal $x(t)$ with the amplitude values | ||
| + | *$1\hspace{0.03cm}\rm V$ $($for symbol $\rm L)$, | ||
| + | *$3\hspace{0.03cm}\rm V$ $($for symbol $\rm H)$ | ||
| + | |||
| + | |||
| + | and the probabilities of occurrence $p_{\rm L} = 0.2$ resp. $p_{\rm H} = 0.8$ results for the second moment: | ||
| + | :$$m_2 = 0.2 \cdot (1\,{\rm V})^2+ 0.8 \cdot (3\,{\rm V})^2 = 7.4 \hspace{0.1cm}{\rm V}^2,$$ | ||
| + | |||
| + | #The rms value $x_{\rm eff}=\sqrt{m_2}=2.72\,{\rm V}$ is independent of the reference resistance $R$ unlike the total power. | ||
| + | #For the latter, with $R=1 \hspace{0.1cm} Ω$ the value $P=m_2/R=7.4 \hspace{0.1cm}{\rm W}$, with $R=50 \hspace{0.1cm} Ω$ on the other hand, only $P=0.148 \hspace{0.1cm}{\rm W}$. | ||
| + | |||
| + | |||
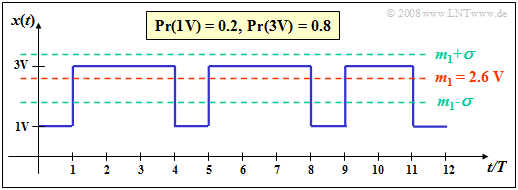
| + | With the DC component $m_1 = 2.6 \hspace{0.05cm}\rm V$ $($see [[Theory_of_Stochastic_Signals/Moments_of_a_Discrete_Random_Variable#First_order_moment_.E2.80.93_linear_mean_.E2.80.93_DC_component|$\text{Example 1})$]] it follows for | ||
| + | *the variance $ σ^2 = 7.4 \hspace{0.05cm}{\rm V}^2 - \big [2.6 \hspace{0.05cm}\rm V\big ]^2 = 0.64\hspace{0.05cm} {\rm V}^2$, | ||
| + | |||
| + | *the standard deviation $σ = 0.8 \hspace{0.05cm} \rm V$. | ||
| + | |||
| + | |||
| + | The same variance $ σ^2 = 0.64\hspace{0.05cm} {\rm V}^2$ and the same standard deviation $σ = 0.8 \hspace{0.05cm} \rm V$ result for the amplitudes $0\hspace{0.05cm}\rm V$ $($for symbol $\rm L)$ and $2\hspace{0.05cm}\rm V$ $($for symbol $\rm H)$, provided the occurrence probabilities $p_{\rm L} = 0.2$ and $p_{\rm H} = 0.8$ remain the same. Only the DC component and the total power change: | ||
| + | :$$m_1 = 1.6 \hspace{0.05cm}{\rm V}, $$ | ||
| + | :$$P = {m_1}^2 +\sigma^2 = 3.2 \hspace{0.05cm}{\rm V}^2.$$}} | ||
| + | |||
| + | |||
| + | ==Exercises for the chapter== | ||
| + | <br> | ||
| + | [[Aufgaben:Exercise_2.2:_Multi-Level_Signals|Exercise 2.2: Multi-Level Signals]] | ||
| − | [[ | + | [[Aufgaben:Exercise_2.2Z:_Discrete_Random_Variables|Exercise 2.2Z: Discrete Random Variables]] |
| − | |||
| − | |||
{{Display}} | {{Display}} | ||
Latest revision as of 19:40, 6 February 2024
Contents
Calculation as ensemble average or time average
The probabilities and the relative frequencies provide extensive information about a discrete random variable. Reduced information is obtained by the so-called »moments« $m_k$, where $k$ represents a natural number.
$\text{Two alternative ways of calculation:}$
Under the condition »$\text{ergodicity}$« implicitly assumed here, there are two different calculation possibilities for the $k$-th order moment:
$\rm (A)$ the »ensemble averaging« or »expected value formation« ⇒ averaging over all possible values $\{ z_\mu\}$ with index $\mu = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , M$:
- $$m_k = {\rm E} \big[z^k \big] = \sum_{\mu = 1}^{M}p_\mu \cdot z_\mu^k \hspace{2cm} \rm with \hspace{0.1cm} {\rm E\big[\text{ ...} \big]\hspace{-0.1cm}:} \hspace{0.3cm} \rm expected\hspace{0.1cm}value ;$$
$\rm (B)$ the »time averaging« over the random sequence $\langle z_ν\rangle$ with index $ν = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , N$:
- $$m_k=\overline{z_\nu^k}=\hspace{0.01cm}\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=\rm 1}^{\it N}z_\nu^k\hspace{1.7cm}\rm with\hspace{0.1cm}horizontal\hspace{0.1cm}line\hspace{-0.1cm}:\hspace{0.1cm}time\hspace{0.1cm}average.$$
Note:
- Both types of calculations lead to the same asymptotic result for sufficiently large values of $N$.
- For finite $N$, a comparable error results as when the probability is approximated by the relative frequency.
First order moment – linear mean – DC component
$\text{Definition:}$ With $k = 1$ we obtain from the general equation the first order moment ⇒ the »linear mean«:
- $$m_1 =\sum_{\mu=1}^{M}p_\mu\cdot z_\mu =\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=1}^{N}z_\nu.$$
- The left part of this equation describes the ensemble averaging $($over all possible values$)$.
- The right equation gives the determination as time average.
- In the context of signals, this quantity is also referred to as the »$\text{direct current}$« $\rm (DC)$ component.
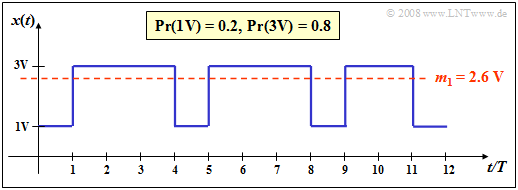
$\text{Example 1:}$ A binary signal $x(t)$ with the two possible values
- $1\hspace{0.03cm}\rm V$ $($for symbol $\rm L)$,
- $3\hspace{0.03cm}\rm V$ $($for symbol $\rm H)$
as well as the occurrence probabilities $p_{\rm L} = 0.2$ and $p_{\rm H} = 0.8$ has the linear mean $($»DC component«$)$
- $$m_1 = 0.2 \cdot 1\,{\rm V}+ 0.8 \cdot 3\,{\rm V}= 2.6 \,{\rm V}. $$
This is drawn as a red line in the graph.
If we determine this parameter by time averaging over the displayed $N = 12$ signal values, we obtain a slightly smaller value:
- $$m_1\hspace{0.01cm}' = 4/12 \cdot 1\,{\rm V}+ 8/12 \cdot 3\,{\rm V}= 2.33 \,{\rm V}. $$
- Here, the probabilities $p_{\rm L} = 0.2$ and $p_{\rm H} = 0.8$ were replaced by the corresponding frequencies $h_{\rm L} = 4/12$ and $h_{\rm H} = 8/12$ respectively.
- In this example the relative error due to insufficient sequence length $N$ is greater than $10\%$.
$\text{Note about our (admittedly somewhat unusual) nomenclature:}$
We denote binary symbols here as in circuit theory with $\rm L$ $($Low$)$ and $\rm H$ $($High$)$ to avoid confusion.
- In coding theory, it is useful to map $\{ \text{L, H}\}$ to $\{0, 1\}$ to take advantage of the possibilities of modulo algebra.
- In contrast, to describe modulation with bipolar $($antipodal$)$ signals, one better chooses the mapping $\{ \text{L, H}\}$ ⇔ $ \{-1, +1\}$.
Second order moment – power – variance – standard deviation
$\text{Definitions:}$
$\rm (A)$ Analogous to the linear mean, $k = 2$ obtains the »second order moment«:
- $$m_2 =\sum_{\mu=\rm 1}^{\it M}p_\mu\cdot z_\mu^2 =\lim_{N\to\infty}\frac{\rm 1}{\it N}\sum_{\nu=\rm 1}^{\it N}z_\nu^2.$$
$\rm (B)$ Together with the DC component $m_1$ the »variance« $σ^2$ can be determined from this as a further parameter $($»Steiner's theorem«$)$:
- $$\sigma^2=m_2-m_1^2.$$
$\rm (C)$ The »standard deviation« $σ$ is the square root of the variance:
- $$\sigma=\sqrt{m_2-m_1^2}.$$
$\text{Notes on units:}$
- For a random signal $x(t)$ ⇒ the second moment $m_2$ gives the total power $($DC power plus AC power$)$ related to the resistance $1 \hspace{0.03cm} Ω$.
- If $x(t)$ describes a voltage, accordingly $m_2$ has the unit ${\rm V}^2$ and the rms value $($»root mean square«$)$ $x_{\rm eff}=\sqrt{m_2}$ has the unit ${\rm V}$.
- The total power for any reference resistance $R$ is calculated to $P=m_2/R$ and accordingly has the unit $\rm V^2/(V/A) = W$.
- If $x(t)$ describes a current waveform, then $m_2$ has the unit ${\rm A}^2$ and the rms value $x_{\rm eff}=\sqrt{m_2}$ has the unit ${\rm A}$.
- The total power for any reference resistance $R$ is calculated to $P=m_2\cdot R$ and accordingly has the unit $\rm A^2 \cdot(V/A) = W$.
- Only in the special case $m_1=0$ ⇒ the variance is $σ^2=m_2$. Then the standard deviation $σ$ coincides also with the rms value $x_{\rm eff}$ .
⇒ The following $($German language$)$ learning video illustrates the defined quantities using the example of a digital signal:
»Momentenberechnung bei diskreten Zufallsgrößen» ⇒ »Moment Calculation for Discrete Random Variables».
$\text{Example 2:}$ For a binary signal $x(t)$ with the amplitude values
- $1\hspace{0.03cm}\rm V$ $($for symbol $\rm L)$,
- $3\hspace{0.03cm}\rm V$ $($for symbol $\rm H)$
and the probabilities of occurrence $p_{\rm L} = 0.2$ resp. $p_{\rm H} = 0.8$ results for the second moment:
- $$m_2 = 0.2 \cdot (1\,{\rm V})^2+ 0.8 \cdot (3\,{\rm V})^2 = 7.4 \hspace{0.1cm}{\rm V}^2,$$
- The rms value $x_{\rm eff}=\sqrt{m_2}=2.72\,{\rm V}$ is independent of the reference resistance $R$ unlike the total power.
- For the latter, with $R=1 \hspace{0.1cm} Ω$ the value $P=m_2/R=7.4 \hspace{0.1cm}{\rm W}$, with $R=50 \hspace{0.1cm} Ω$ on the other hand, only $P=0.148 \hspace{0.1cm}{\rm W}$.
With the DC component $m_1 = 2.6 \hspace{0.05cm}\rm V$ $($see $\text{Example 1})$ it follows for
- the variance $ σ^2 = 7.4 \hspace{0.05cm}{\rm V}^2 - \big [2.6 \hspace{0.05cm}\rm V\big ]^2 = 0.64\hspace{0.05cm} {\rm V}^2$,
- the standard deviation $σ = 0.8 \hspace{0.05cm} \rm V$.
The same variance $ σ^2 = 0.64\hspace{0.05cm} {\rm V}^2$ and the same standard deviation $σ = 0.8 \hspace{0.05cm} \rm V$ result for the amplitudes $0\hspace{0.05cm}\rm V$ $($for symbol $\rm L)$ and $2\hspace{0.05cm}\rm V$ $($for symbol $\rm H)$, provided the occurrence probabilities $p_{\rm L} = 0.2$ and $p_{\rm H} = 0.8$ remain the same. Only the DC component and the total power change:
- $$m_1 = 1.6 \hspace{0.05cm}{\rm V}, $$
- $$P = {m_1}^2 +\sigma^2 = 3.2 \hspace{0.05cm}{\rm V}^2.$$
Exercises for the chapter
Exercise 2.2: Multi-Level Signals
Exercise 2.2Z: Discrete Random Variables