Difference between revisions of "Theory of Stochastic Signals/Set Theory Basics"
| Line 206: | Line 206: | ||
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Two sets $A$ and $B$ are called '''disjoint''' oder '''incompatible''' (miteinander unvereinbar?), |
| − | * | + | *if there is no single element, |
| − | * | + | *that is contained in both $A$ and $B$ .}} |
[[File:EN_Sto_T_1_2_S7.png |frame| Disjunkte Mengen im Venndiagramm | rechts]] | [[File:EN_Sto_T_1_2_S7.png |frame| Disjunkte Mengen im Venndiagramm | rechts]] | ||
| − | + | The diagram shows two disjoint sets $A$ and $B$ in the Venn diagram. | |
| − | In | + | In this special case, the following statements hold: |
| − | * | + | |
| + | *The intersection of two disjoint sets $A$ and $B$ always yields the empty set: | ||
:$${\rm Pr}(A \cap B) = {\rm Pr}(\phi) = \rm 0.$$ | :$${\rm Pr}(A \cap B) = {\rm Pr}(\phi) = \rm 0.$$ | ||
| − | * | + | *The probability of the union set of two disjoint sets $A$ and $B$ is always equal to the sum of the two individual probabilities: |
:$${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B).$$ | :$${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B).$$ | ||
<br clear=all> | <br clear=all> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 6:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. |
| − | * $A :=$ | + | Bei unserem Standardexperiment sind die beiden Mengen |
| − | * $B :=$ | + | * $A :=$ „the outcome is smaller than $3$”$ = \{1, 2\}$ ⇒ ${\rm Pr}( A) = 2/6$, and |
| + | * $B :=$ „the outcome is greater than $3$” $ = \{4, 5,6\}$ ⇒ ${\rm Pr}( B) = 3/6$ | ||
| − | + | disjoint to each other, since $A$ and $B$ do not contain a single common element. | |
| − | * | + | *The intersection yields the empty set: ${A \cap B} = \phi$. |
| − | * | + | *The probability of the union set ${A \cup B} = \{1, 2, 4, 5, 6\}$ is equal to ${\rm Pr}( A) + {\rm Pr}(B) = 5/6.$}} |
| − | == | + | ==Addition rule== |
<br> | <br> | ||
| − | + | Only for disjoint sets $A$ and $B$ the relation ${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B)$ holds for the probability of the union set. But how is this probability calculated for general events that are not necessarily disjoint? | |
| − | [[File:EN_Sto_T_1_2_S8.png | right|frame| | + | [[File:EN_Sto_T_1_2_S8.png | right|frame| About the addition theorem of the probability calculus]] |
| − | + | Consider the right-hand Venn diagram with the intersection $A ∩ B$ shown in purple. | |
| − | * | + | *The red set contains all the elements that belong to $A$ but not to $B$. |
| − | * | + | *The elements of $B$, that are not simultaneously contained in $A$ are shown in blue. |
| − | * | + | *All red, blue, and purple surfaces together make up the union set $A ∪ B$. |
| − | + | From this set-theoretic representation, one can see the following relationships: | |
:$${\rm Pr}(A) \hspace{0.8cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$ | :$${\rm Pr}(A) \hspace{0.8cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$ | ||
:$${\rm Pr}(B) \hspace{0.8cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$ | :$${\rm Pr}(B) \hspace{0.8cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$ | ||
:$${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) \rm + {\rm Pr}(\overline{A} \cap {B}).$$ | :$${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) \rm + {\rm Pr}(\overline{A} \cap {B}).$$ | ||
| − | + | Adding the first two equations and subtracting from them the third, we get: | |
:$${\rm Pr}(A) \rm +{\rm Pr}(B) -{\rm Pr}(A \cup B) = {\rm Pr}(A \cap B).$$ | :$${\rm Pr}(A) \rm +{\rm Pr}(B) -{\rm Pr}(A \cup B) = {\rm Pr}(A \cap B).$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ By rearranging this equation, one arrives at the so-called ''Addition Rule'' for any two, not necessarily disjoint events: |
:$${\rm Pr}(A \cup B) = {\rm Pr}(A) + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$}} | :$${\rm Pr}(A \cup B) = {\rm Pr}(A) + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$}} | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 7:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. |
| − | * $A :=$ | + | Wir betrachten die beiden Mengen |
| − | * $B :=$ | + | * $A :=$ „the outcome is uneven” $= \{1, 3, 5\}$ ⇒ ${\rm Pr}(A) = 3/6$, und |
| + | * $B :=$ „the outcome is greater than $2$”$ = \{3, 4, 5, 6\}$ ⇒ ${\rm Pr}(B) = 4/6$. | ||
| − | + | This gives the following probabilities | |
| − | * | + | *of the union ⇒ ${\rm Pr}(A ∪ B) = 5/6$, and |
| − | * | + | *of the intersection ⇒ ${\rm Pr}(A ∩ B) = 2/6$. |
| − | + | The numerical values show the validity of the addition theorem: $5/6 = 3/6 + 4/6 − 2/6$.}} | |
| − | == | + | ==Complete system== |
<br> | <br> | ||
| − | + | In the last section to this chapter, we again consider more than two possible events, namely, in general, $I$. These events will be denoted by $A_i$ in what follows, and the running index is: $1 ≤ i ≤ I$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ A constellation with events $A_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_i, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_I$ is called a '''complete system''', if and only if the following two conditions are satisfied: |
| − | '''(1)''' | + | '''(1)''' All events are pairwise disjoint: |
:$$A_i \cap A_j = \it \phi \hspace{0.15cm}\rm f\ddot{u}r\hspace{0.15cm}alle\hspace{0.15cm}\it i \ne j.$$ | :$$A_i \cap A_j = \it \phi \hspace{0.15cm}\rm f\ddot{u}r\hspace{0.15cm}alle\hspace{0.15cm}\it i \ne j.$$ | ||
| − | '''(2)''' | + | '''(2)''' The union of all event sets gives the basic set: |
:$$\bigcup_{i=1}^{I} A_i = G.$$}} | :$$\bigcup_{i=1}^{I} A_i = G.$$}} | ||
| − | + | Given these two assumptions, the sum of all probabilities is then: | |
:$$\sum_{i =1}^{ I} {\rm Pr}(A_i) = 1.$$ | :$$\sum_{i =1}^{ I} {\rm Pr}(A_i) = 1.$$ | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 8:}$ The event sets $A_1 := \{1, 5\}$ and $A_2 := \{2, 3\}$ together with the set $A_3 := \{4, 6\}$ result in a complete system in the random experiment "throwing a die", but not in the experiment "throwing a roulette ball".}} |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 9:}$ Another example of a complete system is the discrete random variable $X = \{ x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ with the likelihood corresponding to the following [[Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables#Probability_mass_function_and_probability_density_function|probability function]]: |
:$$P_X(X) = \big [ \hspace{0.1cm} P_X(x_1), P_X(x_2), \hspace{0.05cm}\text{...}\hspace{0.15cm}, P_X(x_I) \hspace{0.05cm} \big ] = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_I \hspace{0.05cm} \big ] \hspace{0.05cm}$$ | :$$P_X(X) = \big [ \hspace{0.1cm} P_X(x_1), P_X(x_2), \hspace{0.05cm}\text{...}\hspace{0.15cm}, P_X(x_I) \hspace{0.05cm} \big ] = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_I \hspace{0.05cm} \big ] \hspace{0.05cm}$$ | ||
:$$\Rightarrow \hspace{0.3cm} p_1 = P_X(x_1) = {\rm Pr}(X=x_1) \hspace{0.05cm}, | :$$\Rightarrow \hspace{0.3cm} p_1 = P_X(x_1) = {\rm Pr}(X=x_1) \hspace{0.05cm}, | ||
\hspace{0.2cm}p_2 = {\rm Pr}(X=x_2) \hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.15cm},\hspace{0.2cm} p_I = {\rm Pr}(X=x_I) \hspace{0.05cm}.$$ | \hspace{0.2cm}p_2 = {\rm Pr}(X=x_2) \hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.15cm},\hspace{0.2cm} p_I = {\rm Pr}(X=x_I) \hspace{0.05cm}.$$ | ||
| − | + | The possible outcomes $x_i$ of the random variable $X$ are pairwise disjoint to each other and the sum of all likelihoods $p_1 + p_2 + \hspace{0.1cm}\text{...}\hspace{0.1cm} + \hspace{0.05cm} p_I$ always yields the result $1$.}} | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 10:}$ Let $X= \{0, 1, 2 \}$ and $P_X (X) = \big[0.2, \ 0.5, \ 0.3\big]$. Then holds: |
:$${\rm Pr}(X=0) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=1) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=2) = 0.3 \hspace{0.05cm}.$$ | :$${\rm Pr}(X=0) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=1) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=2) = 0.3 \hspace{0.05cm}.$$ | ||
| − | + | With random variable $X = \{1, \pi, {\rm e} \}$ and equal $P_X(X) = \big[0.2, \ 0.5, \ 0.3\big]$ the assignments are: | |
:$${\rm Pr}(X=1) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=\pi) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X={\rm e}) = 0.3 \hspace{0.05cm}.$$ | :$${\rm Pr}(X=1) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=\pi) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X={\rm e}) = 0.3 \hspace{0.05cm}.$$ | ||
| − | + | Hints: | |
| − | * | + | *The [[Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables#Probability_mass_function_and_probability_density_function|probability function]] $P_X(X)$ only makes statements about the probabilities, not about the set of values $\{x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ of the random variable $X$. |
| − | * | + | *This additional information is provided by the [[Theory_of_Stochastic_Signals/Probability_Density_Function_(PDF)#Definition_der_Wahrscheinlichkeitsdichtefunktion|probability density function]] (PDF).}} |
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
[[Aufgaben:1.2 Schaltlogik (D/B-Wandler)|Aufgabe 1.2: Schaltlogik (D/B-Wandler)]] | [[Aufgaben:1.2 Schaltlogik (D/B-Wandler)|Aufgabe 1.2: Schaltlogik (D/B-Wandler)]] | ||
Revision as of 00:14, 15 November 2021
Contents
Venn diagram, universal and empty set
In later chapters, we will sometimes refer to set theory . Therefore, the most important basics and definitions of this discipline will be briefly summarized here. The topic is also covered in the (German language) learning video
"Mengentheoretische Begriffe und Gesetzmäßigkeiten" ⇒ "Set Theory – Terms and Regularities"
An important tool of set theory is the Venn diagramm according to the graph:
- Applied to probability theory, here the events $A_i$ are represented as areas. For a simpler description we do not denote the events here with $A_1$, $A_2$ and $A_3$, but with $A$, $B$ and $C$ in contrast to the last chapter.
- The total area corresponds to the "universal set" (or short: "universe") $G$. The universe $G$ contains all possible outcomes and stands for the certain event, which by definition occurs with probability „one”: ${\rm Pr}(G) = 1$. For example, in the random experiment "Throwing a die", the probability for the event "The number of eyes is less than or equal to 6" is identical to one.
- In contrast, the empty set $ϕ$ does not contain a single element. In terms of events, the empty set specifies the impossible event with probability ${\rm Pr}(ϕ) = 0$ an. For example, in the experiment "Throwing a die", the probability for the event "The number of eyes is greater than 6" is identically zero.
Note that not every event $A$ with ${\rm Pr}(A) = 0$ can really never happen. For example:
- The event "The noise value $n$ is identically zero" is vanishingly small and ${\rm Pr}(n \equiv 0) = 0$, if $n$ is described by a continuous (Gaussian) random variable.
- Nevertheless, it is of course possible (although extremely unlikely) that at some point the exact noise value $n = 0$ will also occur.
Union set
Some set-theoretical relationss are explained now on the basis of the Venn diagram.
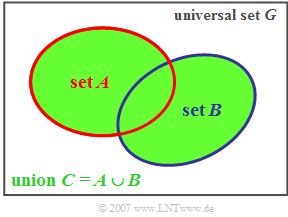
$\text{Definition:}$ The union set $C$ of two sets $A$ and $B$ contains all the elements that are contained either in set $A$ or in set $B$ or in both.
- This relationship is expressed as the following formula:
$$\ C = A \cup B \hspace{0.2cm}(= A + B).$$
- In the literature, especially in the Galois field $\rm GF(2)$ the term "sumset" is common, and the plus sign is sometimes used.
- For example, in our tutorial we use this term in the book "Channel Coding".
Using the diagram, it is easy to see the following laws of set theory:
- $$A \cup \it \phi = A \rm \hspace{3.6cm}(union \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}empty \hspace{0.15cm}set),$$
- $$A\cup G = G \rm \hspace{3.6cm}(union \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}universe),$$
- $$A\cup A = A \hspace{3.6cm}(\rm tautology),$$
- $$A\cup B = B\cup A \hspace{2.75cm}(\rm commutative \hspace{0.15cm}property),$$
- $$(A\cup B)\cup C = A\cup (B\cup C) \hspace{0.45cm}(\rm associative \hspace{0.15cm}property).$$
If nothing else is known about the event sets $A$ and $B$ then only a lower bound and an upper bound can be given for the probability of the union set:
- $${\rm Max}\big({\rm Pr} (A), \ {\rm Pr} (B)\big) \le {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B).$$
- The probability of the union set is equal to the lower bound if $A$ is a subset of $B$ or vice versa.
- The upper bound holds for disjoint sets.
$\text{Example 1:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Consider the two events
- $A :=$ "The outcome is greater than or equal to $5$"$ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$,
- $B :=$ "The outcome is even" $= \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$,
then the union set contains four elements: $(A \cup B) = \{2, 4, 5, 6 \}$ ⇒ ${\rm Pr} (A \cup B) = 4/6 = 2/3$.
- For the lower bound: ${\rm Pr} (A \cup B) \ge {\rm Max}\big({\rm Pr} (A),\ {\rm Pr} (B)\big ) = 3/6.$
- For the upper bound: $ {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B) = 5/6.$
Intersection set
Another important set-theoretic linkage is the intersection.
$\text{Definition:}$ The intersection set $C$ of two sets $A$ and $B$ contains all those elements which are contained in both the set $A$ and the set $B$.
- This relationship is expressed as the following formula:
- $$C = A \cap B \hspace{0.2cm}(= A \cdot B).$$
- In the literature, especially in the Galois field $\rm GF(2)$ the term "Cartesian product" is also common, and the multiplication sign is sometimes used.
- For example, in our tutorial we use this term in the book "Channel Coding".
In the diagram, the intersection is shown in purple. Analog to the union set, the following regularities are to be mentioned here:
- $$A \cap \it \phi = \it \phi \rm \hspace{3.75cm}(intersection \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}empty \hspace{0.15cm}set),$$
- $$A \cap G = A \rm \hspace{3.6cm}(intersection \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}universe),$$
- $$A\cap A = A \rm \hspace{3.6cm}(tautology),$$
- $$A\cap B = B\cap A \rm \hspace{2.75cm}(commutative \hspace{0.15cm}property),$$
- $$(A\cap B)\cap C = A\cap (B\cap C) \rm \hspace{0.45cm}(associative \hspace{0.15cm}property).$$
- If nothing else is known about $A$ and $B$ , then no statement can be made for the probability of the intersection.
- However, if ${\rm Pr} (A) \le 1/2$ and at the same time ${\rm Pr} (B) \le 1/2$ hold, then a lower bound and an upper bound can be given:
- $$0 \le {\rm Pr} (A ∩ B) \le {\rm Min}\ \big({\rm Pr} (A),\ {\rm Pr} (B)\big ).$$
- ${\rm Pr}(A ∩ B)$ is sometimes called the "joint probability" and is denoted by ${\rm Pr}(A, \ B)$ .
- ${\rm Pr}(A ∩ B)$ is equal to the upper bound if $A$ is a subset of $B$ or vice versa.
- The lower bound is obtained for the joint probability of disjoint sets.
$\text{Example 2:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. Consider the two events
- $A :=$ „the outcome is greater than or equal to $5$”$ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$, und
- $B :=$ „the outcome is even”$ = \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$,
The intersection contains only one element: $(A ∩ B) = \{ 6 \}$ ⇒ ${\rm Pr} (A ∩ B) = 1/6$.
- The upper bound is obtained as ${\rm Pr} (A ∩ B) \le {\rm Min}\ \big ({\rm Pr} (A), \, {\rm Pr} (B)\big ) = 2/6.$
- The lower bound of the intersection here is zero because of ${\rm Pr} (A) \le 1/2$ and ${\rm Pr} (B) \le 1/2$ .
Complementary set
$\text{Definition:}$ The complementary set of $A$ is often denoted by a straight line above the letter $(\overline{A})$ . It contains all the elements that are not contained in the set $A$ and it holds for their probability:
- $${\rm Pr}(\overline{A}) = 1- {\rm Pr}(A).$$
In the Venn diagram shown, the set complementary to $A$ is shaded. From this diagram, some set-theoretic relationships can be seen:
- The complementary set of the complementary set of $A$ is the set $A$ itself:
- $$\overline{\overline{A}} = A.$$
- The union of a set $A$ with its complementary set gives the universal set:
- $${\rm Pr}(A \cup \overline{A}) = {\rm Pr}(G) = \rm 1.$$
- The intersection of $A$ with its complementary set gives the empty set:
- $${\rm Pr}(A \cap \overline{A}) = {\rm Pr}({\it \phi}) \rm = 0.$$
$\text{Example 3:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. Starting from the set
- $A :=$ „the outcome is smaller than $5$” $= \{1, 2, 3, 4\}$ ⇒ ${\rm Pr} (A)= 2/3$
the corresponding complementary set is
- $\overline{A} :=$ „the outcome is greater than or equal to $5$”$ = \{5, 6\}$ ⇒ ${\rm Pr} (\overline{A})= 1 - {\rm Pr} (A) = 1 - 2/3 = 1/3.$
Strict subset – improper subset
$\text{Definitions:}$ One calls $A$ a strict subset of $B$ and writes for this $A ⊂ B$,
- if all elements of $A$ are also contained in $B$ ,
- but not all elements of $B$ are also contained in $A$.
In this case, the probabilities are:
- $${\rm Pr}(A) < {\rm Pr}(B).$$
This set-theoretic relation is illustrated by the sketched Venn diagram.
On the other hand, $A$ is called a subset of $B$ and uses the notation
- $$A \subseteq B = (A \subset B) \cup (A = B),$$
wenn $A$ entweder eine echte Teilmenge von $B$ ist oder wenn $A$ und $B$ gleiche Mengen sind.
- The relation ${\rm Pr} (A) \le {\rm Pr} (B)$ then applies to the probabilities.
- The equality sign is only valid for the special case $A = B$.
In addition, however, the two equations known as the laws of absorption also apply:
- $$(A \cap B) \cup A = A ,$$
- $$(A \cup B) \cap A = A,$$
since the intersection $A ∩ B$ is always a subset of $A$ , but at the same time $A$ is also a subset of the union $A ∪ B$ .
$\text{Example 4:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. Consider the two events
- $A :=$ „the outcome is uneven”$ = \{1, 3, 5\}$ ⇒ ${\rm Pr} (A)= 3/6$, und
- $B :=$ „the outcome is a prime number” $= \{1, 2, 3, 5\}$ ⇒ ${\rm Pr} (B)= 4/6$.
It can be seen that $A$ is a (strict) subset of the set $B$ . Accordingly, ${\rm Pr} (A) < {\rm Pr} (B)$ is also true.
Theorems of de Morgan
In many set theory tasks, de Morgan's two theorems are extremely useful. These are:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B},$$
- $$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$
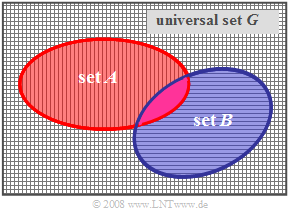
These regularities are illustrated in the diagram:
- Set $A$ is shown in red and set $B$ is shown in blue.
- The complimentary set $\overline {A}$ of $A$ is shaded in the horizontal direction.
- The complimentary set $\overline {B}$ of $B$ is hatched in the vertical direction.
- The complement $\overline{A \cup B}$ of the union ${A \cup B}$ is hatched both horizontally and vertically.
- It is thus equal to the intersection $\overline{A} \cap \overline{B}$ of the two complement sets of $A$ and $B$:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B}.$$
The second form of the de Morgan theorem can also be illustrated graphically with this Venn diagram:
- The intersection $A ∩ B$ (shown in purple in the figure) is neither horizontally nor vertically shaded.
- Accordingly, the complement $\overline{A ∩ B}$ of the intersection is hatched either horizontally, vertically, or in both directions.
- By de Morgan's second theorem, the complement of the intersection equals the union of the two complementary sets of $A$ and $B$:
- $$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$
$\text{Example 5:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. We consider the two sets
- $A : =$ „the outcome is uneven” $= \{1, 3, 5\}$,
- $B : =$ „the outcome is greater than $2$” $= \{3, 4, 5, 6\}$.
From this follow the two complementary sets
- $\overline {A} : =$ „the outcome” $= \{2, 4, 6\}$,
- $\overline {B} : =$ „the outcome is smaller than $3$” $= \{1, 2\}$.
Further, using the above theorems, we obtain the following subsets:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B} = \{2\}\hspace{0.5 cm}\rm und \hspace{0.5cm} \overline{\it A \cap \it B} =\overline{\it A} \cup \overline{\it B} = \{1,2,4,6\}.$$
Disjoint sets
$\text{Definition:}$ Two sets $A$ and $B$ are called disjoint oder incompatible (miteinander unvereinbar?),
- if there is no single element,
- that is contained in both $A$ and $B$ .
The diagram shows two disjoint sets $A$ and $B$ in the Venn diagram.
In this special case, the following statements hold:
- The intersection of two disjoint sets $A$ and $B$ always yields the empty set:
- $${\rm Pr}(A \cap B) = {\rm Pr}(\phi) = \rm 0.$$
- The probability of the union set of two disjoint sets $A$ and $B$ is always equal to the sum of the two individual probabilities:
- $${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B).$$
$\text{Example 6:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. Bei unserem Standardexperiment sind die beiden Mengen
- $A :=$ „the outcome is smaller than $3$”$ = \{1, 2\}$ ⇒ ${\rm Pr}( A) = 2/6$, and
- $B :=$ „the outcome is greater than $3$” $ = \{4, 5,6\}$ ⇒ ${\rm Pr}( B) = 3/6$
disjoint to each other, since $A$ and $B$ do not contain a single common element.
- The intersection yields the empty set: ${A \cap B} = \phi$.
- The probability of the union set ${A \cup B} = \{1, 2, 4, 5, 6\}$ is equal to ${\rm Pr}( A) + {\rm Pr}(B) = 5/6.$
Addition rule
Only for disjoint sets $A$ and $B$ the relation ${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B)$ holds for the probability of the union set. But how is this probability calculated for general events that are not necessarily disjoint?
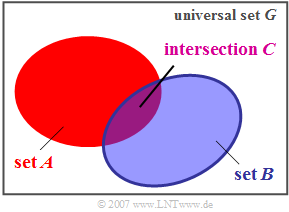
Consider the right-hand Venn diagram with the intersection $A ∩ B$ shown in purple.
- The red set contains all the elements that belong to $A$ but not to $B$.
- The elements of $B$, that are not simultaneously contained in $A$ are shown in blue.
- All red, blue, and purple surfaces together make up the union set $A ∪ B$.
From this set-theoretic representation, one can see the following relationships:
- $${\rm Pr}(A) \hspace{0.8cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$
- $${\rm Pr}(B) \hspace{0.8cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$
- $${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) \rm + {\rm Pr}(\overline{A} \cap {B}).$$
Adding the first two equations and subtracting from them the third, we get:
- $${\rm Pr}(A) \rm +{\rm Pr}(B) -{\rm Pr}(A \cup B) = {\rm Pr}(A \cap B).$$
$\text{Definition:}$ By rearranging this equation, one arrives at the so-called Addition Rule for any two, not necessarily disjoint events:
- $${\rm Pr}(A \cup B) = {\rm Pr}(A) + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$
$\text{Example 7:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. Wir betrachten die beiden Mengen
- $A :=$ „the outcome is uneven” $= \{1, 3, 5\}$ ⇒ ${\rm Pr}(A) = 3/6$, und
- $B :=$ „the outcome is greater than $2$”$ = \{3, 4, 5, 6\}$ ⇒ ${\rm Pr}(B) = 4/6$.
This gives the following probabilities
- of the union ⇒ ${\rm Pr}(A ∪ B) = 5/6$, and
- of the intersection ⇒ ${\rm Pr}(A ∩ B) = 2/6$.
The numerical values show the validity of the addition theorem: $5/6 = 3/6 + 4/6 − 2/6$.
Complete system
In the last section to this chapter, we again consider more than two possible events, namely, in general, $I$. These events will be denoted by $A_i$ in what follows, and the running index is: $1 ≤ i ≤ I$.
$\text{Definition:}$ A constellation with events $A_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_i, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_I$ is called a complete system, if and only if the following two conditions are satisfied:
(1) All events are pairwise disjoint:
- $$A_i \cap A_j = \it \phi \hspace{0.15cm}\rm f\ddot{u}r\hspace{0.15cm}alle\hspace{0.15cm}\it i \ne j.$$
(2) The union of all event sets gives the basic set:
- $$\bigcup_{i=1}^{I} A_i = G.$$
Given these two assumptions, the sum of all probabilities is then:
- $$\sum_{i =1}^{ I} {\rm Pr}(A_i) = 1.$$
$\text{Example 8:}$ The event sets $A_1 := \{1, 5\}$ and $A_2 := \{2, 3\}$ together with the set $A_3 := \{4, 6\}$ result in a complete system in the random experiment "throwing a die", but not in the experiment "throwing a roulette ball".
$\text{Example 9:}$ Another example of a complete system is the discrete random variable $X = \{ x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ with the likelihood corresponding to the following probability function:
- $$P_X(X) = \big [ \hspace{0.1cm} P_X(x_1), P_X(x_2), \hspace{0.05cm}\text{...}\hspace{0.15cm}, P_X(x_I) \hspace{0.05cm} \big ] = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_I \hspace{0.05cm} \big ] \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} p_1 = P_X(x_1) = {\rm Pr}(X=x_1) \hspace{0.05cm}, \hspace{0.2cm}p_2 = {\rm Pr}(X=x_2) \hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.15cm},\hspace{0.2cm} p_I = {\rm Pr}(X=x_I) \hspace{0.05cm}.$$
The possible outcomes $x_i$ of the random variable $X$ are pairwise disjoint to each other and the sum of all likelihoods $p_1 + p_2 + \hspace{0.1cm}\text{...}\hspace{0.1cm} + \hspace{0.05cm} p_I$ always yields the result $1$.
$\text{Example 10:}$ Let $X= \{0, 1, 2 \}$ and $P_X (X) = \big[0.2, \ 0.5, \ 0.3\big]$. Then holds:
- $${\rm Pr}(X=0) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=1) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=2) = 0.3 \hspace{0.05cm}.$$
With random variable $X = \{1, \pi, {\rm e} \}$ and equal $P_X(X) = \big[0.2, \ 0.5, \ 0.3\big]$ the assignments are:
- $${\rm Pr}(X=1) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=\pi) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X={\rm e}) = 0.3 \hspace{0.05cm}.$$
Hints:
- The probability function $P_X(X)$ only makes statements about the probabilities, not about the set of values $\{x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ of the random variable $X$.
- This additional information is provided by the probability density function (PDF).
Exercises for the chapter
Aufgabe 1.2: Schaltlogik (D/B-Wandler)
Aufgabe 1.3: Fiktive Uni Irgenwo
Aufgabe 1.3Z: Gewinnen mit Roulette?