Difference between revisions of "Theory of Stochastic Signals/Set Theory Basics"
| (71 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Probability Calculation |
| − | |Vorherige Seite= | + | |Vorherige Seite=Some Basic Definitions |
| − | |Nächste Seite= | + | |Nächste Seite=Statistical Dependence and Independence |
}} | }} | ||
| − | == | + | ==Venn diagram, universal and empty set== |
| − | In | + | <br> |
| + | In later chapters, we will sometimes refer to [https://en.wikipedia.org/wiki/Set_theory »set theory«] . Therefore, the most important basics and definitions of this discipline will be briefly summarized here. The topic is also covered in the $($German language$)$ learning video [[Mengentheoretische_Begriffe_und_Gesetzmäßigkeiten_(Lernvideo)|»Mengentheoretische Begriffe und Gesetzmäßigkeiten«]] ⇒ »Set Theory – Terms and Regularities«. | ||
| + | [[File:EN_Sto_T_1_2_S1.png | right|frame|Set representation in the Venn diagram]] | ||
| − | + | An important tool of set theory is the »'''Venn diagram'''« according to the graph: | |
| + | *Applied to probability theory, the events $A_i$ are represented here as areas. For a simpler description we do not denote the events here with $A_1$, $A_2$ and $A_3$, but with $A$, $B$ and $C$ in contrast to the last chapter. | ||
| − | + | *The total area corresponds to the »universal set« $($or short: »universe«$)$ $G$. The universe $G$ contains all possible outcomes and stands for the »'''certain event'''«, which by definition occurs with probability »one«: ${\rm Pr}(G) = 1$. For example, in the random experiment »Throwing a die«, the probability for the event »The number of eyes is less than or equal to 6« is identical to one. | |
| + | *In contrast, the »'''empty set'''« $ϕ$ does not contain a single element. In terms of events, the empty set specifies the »'''impossible event'''« with probability ${\rm Pr}(ϕ) = 0$ an. For example, in the experiment »Throwing a die«, the probability for the event »The number of eyes is greater than 6« is identically zero. | ||
| − | |||
| − | + | It should be noted that not every event $A$ with ${\rm Pr}(A) = 0$ can really never occur: | |
| + | *Thus, the probability of the event »the noise value $n$ is identical to zero» is vanishingly small and it applies ${\rm Pr}(n \equiv 0) = 0$, if $n$ is described by a continuous–valued $($Gaussian$)$ random variable. | ||
| − | + | *Nevertheless, it is of course possible $($although extremely unlikely$)$ that at some points the exact noise value $n = 0$ will also occur. | |
| − | + | ==Union set== | |
| + | <br> | ||
| + | Some set-theoretical relations are explained now on the basis of the Venn diagram. | ||
| − | == | + | {{BlaueBox|TEXT= |
| − | + | $\text{Definition:}$ The »'''union set'''« $C$ of two sets $A$ and $B$ contains all the elements that are contained either in set $A$ or in set $B$ or in both. | |
| + | [[File: EN_Sto_T_1_2_S2.png |right|frame| Union set in the Venn diagram]] | ||
| + | *This relationship is expressed as the following formula: | ||
| + | :$$\ C = A \cup B.$$ | ||
| − | {{ | + | *Using the diagram, it is easy to see the following laws of set theory: |
| − | + | :$$A \cup \it \phi = A \rm \hspace{3.6cm}(union \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}empty \hspace{0.15cm}set),$$ | |
| − | $$\ C = A \cup B \hspace{0. | + | :$$A\cup G = G \rm \hspace{3.6cm}(union \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}universe),$$ |
| − | + | :$$A\cup A = A \hspace{3.6cm}(\rm tautology),$$ | |
| + | :$$A\cup B = B\cup A \hspace{2.75cm}(\rm commutative \hspace{0.15cm}property),$$ | ||
| + | :$$(A\cup B)\cup C = A\cup (B\cup C) \hspace{0.45cm}(\rm associative \hspace{0.15cm}property).$$ | ||
| + | *If nothing else is known about the event sets $A$ and $B$ then only a lower bound and an upper bound can be given for the probability of the union set: | ||
| + | :$${\rm Max}\big({\rm Pr} (A), \ {\rm Pr} (B)\big) \le {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B).$$ | ||
| − | + | *The probability of the union set is equal to the lower bound if $A$ is a [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Proper_subset_.E2.80.93_Improper_subset|$\text{subset}$]] of $B$ or vice versa. | |
| + | *The upper bound holds for [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Disjoint_sets|»disjoint sets«]].}} | ||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 1:}$ We consider again the experiment »throwing a die«. The possible outcomes $($number of points$)$ are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. | ||
| − | + | Consider the two events | |
| − | + | * $A :=$ »The outcome is greater than or equal to $5$ « $ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$, | |
| − | $$ | + | |
| − | $ | + | * $B :=$ »The outcome is even « $= \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$, |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | then the union set contains four elements: $(A \cup B) = \{2, 4, 5, 6 \}$ ⇒ ${\rm Pr} (A \cup B) = 4/6 = 2/3$. | |
| + | *For the lower bound: ${\rm Pr} (A \cup B) \ge {\rm Max}\big({\rm Pr} (A),\ {\rm Pr} (B)\big ) = 3/6.$ | ||
| + | *For the upper bound: $ {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B) = 5/6.$}} | ||
| − | + | ==Intersection set== | |
| − | + | <br> | |
| − | + | Another important set-theoretic relation is the intersection. | |
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ The »'''intersection set'''« $C$ of two sets $A$ and $B$ contains all those elements which are contained in both the set $A$ and the set $B$. | ||
| + | [[File:EN_Sto_T_1_2_S3.png |right|frame| Intersection set in the Venn diagram]] | ||
| − | + | *This relationship is expressed as the following formula: | |
| − | + | :$$C = A \cap B.$$ | |
| − | == | + | *In the diagram, the intersection is shown in purple. Analog to the union set, the following regularities apply here: |
| − | + | :$$A \cap \it \phi = \it \phi \rm \hspace{3.75cm}(intersection \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}empty \hspace{0.15cm}set),$$ | |
| + | :$$A \cap G = A \rm \hspace{3.6cm}(intersection \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}universe),$$ | ||
| + | :$$A\cap A = A \rm \hspace{3.6cm}(tautology),$$ | ||
| + | :$$A\cap B = B\cap A \rm \hspace{2.75cm}(commutative \hspace{0.15cm}property),$$ | ||
| + | :$$(A\cap B)\cap C = A\cap (B\cap C) \rm \hspace{0.45cm}(associative \hspace{0.15cm}property).$$ | ||
| − | + | *If nothing else is known about $A$ and $B$, then no statement can be made for the probability of the intersection. | |
| − | |||
| − | |||
| − | |||
| + | *However, if ${\rm Pr} (A) \le 1/2$ and at the same time ${\rm Pr} (B) \le 1/2$ hold, then a lower and an upper bound can be given: | ||
| + | :$$0 \le {\rm Pr} (A ∩ B) \le {\rm Min}\ \big({\rm Pr} (A),\ {\rm Pr} (B)\big ).$$ | ||
| − | + | *${\rm Pr}(A ∩ B)$ is sometimes called the »joint probability« and is denoted by ${\rm Pr}(A, \ B)$. | |
| + | *${\rm Pr}(A ∩ B)$ is equal to the upper bound if $A$ is a [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Proper_subset_.E2.80.93_Improper_subset|$\text{subset}$]] of $B$ or vice versa. | ||
| + | |||
| + | *The lower bound is obtained for the joint probability of [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Disjoint_sets|»disjoint sets«]].}} | ||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 2:}$ We consider again the experiment »throwing a die«. The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. | ||
| − | + | Consider the two events | |
| − | + | * $A :=$ »The outcome is greater than or equal to $5$« $ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$, | |
| − | $$ | ||
| − | |||
| − | |||
| − | |||
| − | + | * $B :=$ »The outcome is even« $ = \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$. | |
| − | $$\ | ||
| − | |||
| − | + | The intersection contains only one element: $(A ∩ B) = \{ 6 \}$ ⇒ ${\rm Pr} (A ∩ B) = 1/6$. | |
| − | + | *The upper bound is obtained as ${\rm Pr} (A ∩ B) \le {\rm Min}\ \big ({\rm Pr} (A), \, {\rm Pr} (B)\big ) = 2/6.$ | |
| − | + | *The lower bound of the intersection is zero because of ${\rm Pr} (A) \le 1/2$ and ${\rm Pr} (B) \le 1/2$ .}} | |
| − | |||
| − | == | + | ==Complementary set== |
| − | {{Definition} | + | <br> |
| − | + | {{BlaueBox|TEXT= | |
| − | $ | + | $\text{Definition:}$ The »'''complementary set'''« of $A$ is often denoted by a straight line above the letter $(\overline{A})$ . It contains all the elements that are not contained in the set $A$ and it holds for their probability: |
| − | + | [[File:EN_Sto_T_1_2_S4Neu.png| right|frame|Complementary set in the Venn diagram]] | |
| + | :$${\rm Pr}(\overline{A}) = 1- {\rm Pr}(A).$$ | ||
| − | + | In the Venn diagram, the set complementary to $A$ is shaded. | |
| + | From this diagram, some set-theoretic relationships can be seen: | ||
| + | *The complementary of the complementary of $A$ is the set $A$ itself: | ||
| + | :$$\overline{\overline{A} } = A.$$ | ||
| + | *The union of a set $A$ with its complementary set gives the universal set: | ||
| + | :$${\rm Pr}(A \cup \overline{A}) = {\rm Pr}(G) = \rm 1.$$ | ||
| + | *The intersection of $A$ with its complementary set gives the empty set: | ||
| + | :$${\rm Pr}(A \cap \overline{A}) = {\rm Pr}({\it \phi}) \rm = 0.$$}} | ||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 3:}$ We consider again the experiment »throwing a die». The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. | ||
| − | + | *Starting from the set | |
| − | + | :$$A :=\text{ »The outcome is smaller than $5$« } = \{1, 2, 3, 4\}\ \ \text{ ⇒ } \ \ {\rm Pr} (A)= 2/3,$$ | |
| − | $$\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {{ | + | *the corresponding complementary set is |
| − | + | :$$\overline{A} :=\text{ »The outcome is greater than or equal to $5$«} = \{5, 6\} \ \ \text{ ⇒ }\ \ {\rm Pr} (\overline{A})= 1 - {\rm Pr} (A) = 1 - 2/3 = 1/3.$$}} | |
| − | |||
| − | == | + | ==Proper subset – Improper subset== |
| − | + | <br> | |
| + | {{BlaueBox|TEXT= | ||
| + | [[File:EN_Sto_T_1_2_S5.png | right|frame| Proper subset in the Venn diagram]] | ||
| + | $\text{Definitions:}$ | ||
| + | '''(1)''' One calls $A$ a »'''proper subset'''« of $B$ and writes for this relationship $A ⊂ B$, | ||
| + | *if all elements of $A$ are also contained in $B$, | ||
| − | + | *but not all elements of $B$ are contained in $A$. | |
| − | + | In this case, for the probabilities hold: | |
| − | + | :$${\rm Pr}(A) < {\rm Pr}(B).$$ | |
| − | $$\rm Pr( | ||
| − | |||
| + | This set-theoretic relationship is illustrated by the sketched Venn diagram on the right. | ||
| − | |||
| − | |||
| − | + | '''(2)''' On the other hand, $A$ is called an »'''improper subset'''« of $B$ and uses the notation | |
| − | + | :$$A \subseteq B = (A \subset B) \cup (A = B),$$ | |
| − | + | if $A$ is either a proper subset of $B$ or if $A$ and $B$ are equal sets. | |
| + | *Then applies to the probabilities: ${\rm Pr} (A) \le {\rm Pr} (B)$. | ||
| − | + | *The equality sign is only valid for the special case $A = B$.}} | |
| − | $ | ||
| − | |||
| − | + | In addition, the two equations known as the »'''absorption laws'''« also apply: | |
| − | + | :$$(A \cap B) \cup A = A ,$$ | |
| − | + | :$$(A \cup B) \cap A = A,$$ | |
| − | + | *since the intersection $A ∩ B$ is always a subset of $A$, | |
| − | + | *but at the same time $A$ is also a subset of the union $A ∪ B$. | |
| − | $ | ||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Example 4:}$ We consider again the experiment »throwing a die«. The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Consider the two events | ||
| + | * $A :=$ »The outcome is odd« $ = \{1, 3, 5\}$ ⇒ ${\rm Pr} (A)= 3/6$, | ||
| − | + | * $B :=$ »The outcome is a prime number» $ = \{1, 2, 3, 5\}$ ⇒ ${\rm Pr} (B)= 4/6$. | |
| − | |||
| − | |||
| − | + | It can be seen that $A$ is a $($proper$)$ subset of $B$. Accordingly, ${\rm Pr} (A) < {\rm Pr} (B)$ is also true. }} | |
| − | |||
| − | |||
| − | |||
| + | ==Theorems of de Morgan== | ||
| + | <br> | ||
| + | In many set-theoretical tasks, the two theorems of [https://en.wikipedia.org/wiki/Augustus_De_Morgan $\text{de Morgan}$] are extremely useful. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Theorem of de Morgan:}$ | ||
| + | [[File:EN_Sto_T_1_2_S6.png|frame| Zu den Theoremen von de Morgan | About de Morgan's theorems]] | ||
| − | + | :$$\overline{A \cup B} = \overline{A} \cap \overline{B},$$ | |
| − | $$\overline{A \cup B} = \overline{A} \cap \overline{B} | + | :$$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$ |
| − | |||
| − | + | These regularities are illustrated in the Venn diagram: | |
| − | {{ | + | #Set $A$ is shown in red and set $B$ is shown in blue. |
| − | + | #The complement $\overline {A}$ of $A$ is hatched in the horizontal direction. | |
| − | {{ | + | #The complement $\overline {B}$ of $B$ is hatched in the vertical direction. |
| + | #The complement $\overline{A \cup B}$ of the union ${A \cup B}$ is hatched both horizontally and vertically. | ||
| + | #It is thus equal to the intersection $\overline{A} \cap \overline{B}$ of the two complement sets of $A$ and $B$: | ||
| + | ::$$\overline{A \cup B} = \overline{A} \cap \overline{B}.$$}} | ||
| − | + | The second form of the de Morgan theorem can also be illustrated graphically with the same Venn diagram: | |
| − | + | #The intersection $A ∩ B$ $($shown in purple in the figure$)$ is neither horizontally nor vertically hatched. | |
| − | + | #Accordingly, the complement $\overline{A ∩ B}$ of the intersection is hatched either horizontally, vertically, or in both directions. | |
| − | + | #By de Morgan's second theorem, the complement of the intersection equals the union of the two complementary sets of $A$ and $B$: | |
| − | $ | + | ::$$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$ |
| − | |||
| − | $$\ | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 5:}$ We consider again the experiment »throwing a die«. The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. | ||
| − | + | We consider the two sets | |
| − | + | * $A : =$ »The outcome is odd« $= \{1, 3, 5\}$, | |
| − | * $A$ = | + | * $B : =$ »The outcome is greater than $2$« $= \{3, 4, 5, 6\}$. |
| − | * $B$ = | ||
| − | |||
| − | |||
| − | + | From this follow the two complementary sets | |
| − | + | * $\overline {A} : =$ »The outcome is even« $= \{2, 4, 6\}$, | |
| + | * $\overline {B} : =$ »The outcome is smaller than $3$« $= \{1, 2\}$. | ||
| − | |||
| − | + | Further, using the above theorems, we obtain the following sets: | |
| + | :$$\overline{A \cup B} = \overline{A} \cap \overline{B} = \{2\},$$ | ||
| + | :$$\overline{\it A \cap \it B} =\overline{\it A} \cup \overline{\it B} = \{1,2,4,6\}.$$}} | ||
| − | + | ==Disjoint sets== | |
| − | + | <br> | |
| − | $$ | + | {{BlaueBox|TEXT= |
| − | $$ | + | [[File:EN_Sto_T_1_2_S7.png |frame| Disjunkte Mengen im Venndiagramm | Disjoint sets in the Venn diagram]] |
| + | |||
| + | $\text{Definition:}$ Two sets $A$ and $B$ are called »'''disjoint'''« or »'''incompatible'''«, | ||
| + | |||
| + | *if there is no single element, | ||
| + | |||
| + | *that is contained in both $A$ and $B$. | ||
| − | |||
| − | |||
| − | + | The diagram shows two disjoint sets $A$ and $B$ in the Venn diagram. | |
| − | $$ | ||
| − | {{ | + | In this special case, the following statements hold: |
| − | + | ||
| − | * $A$ = | + | *The intersection of two disjoint sets $A$ and $B$ always yields the empty set: |
| − | + | :$${\rm Pr}(A \cap B) = {\rm Pr}(\phi) = \rm 0.$$ | |
| + | *The probability of the union set of two disjoint sets $A$ and $B$ is always equal to the sum of the two individual probabilities: | ||
| + | :$${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B).$$}} | ||
| + | <br clear=all> | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 6:}$ We consider again the experiment »throwing a die«. The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. | ||
| + | In our standard experiment, the two sets are now | ||
| + | * $A :=$ »The outcome is smaller than $3$ « $ = \{1, 2\}$ ⇒ ${\rm Pr}( A) = 2/6$, | ||
| + | |||
| + | * $B :=$ »The outcome is greater than $3$ « $ = \{4, 5,6\}$ ⇒ ${\rm Pr}( B) = 3/6$ | ||
| − | |||
| − | |||
| − | |||
| + | disjoint to each other, since $A$ and $B$ do not contain a single common element. | ||
| + | #The intersection yields the empty set: ${A \cap B} = \phi$. | ||
| + | #The probability of the union set ${A \cup B} = \{1, 2, 4, 5, 6\}$ is equal to ${\rm Pr}( A) + {\rm Pr}(B) = 5/6.$}} | ||
| − | + | ==Addition rule== | |
| − | {{ | + | <br> |
| + | Only for disjoint sets $A$ and $B$, the relation ${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B)$ holds for the probability of the union set. But how is this probability calculated for general events that are not necessarily disjoint? | ||
| − | + | [[File:EN_Sto_T_1_2_S8.png | right|frame| »Addition rule« of probability calculus]] | |
| − | + | Consider the right-hand Venn diagram with the intersection $A ∩ B$ shown in purple: | |
| + | #The red set contains all the elements that belong to $A$, but not to $B$. | ||
| + | #The elements of $B$, that are not simultaneously contained in $A$ are shown in blue. | ||
| + | #All red, blue, and purple surfaces together make up the union set $A ∪ B$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | From this set-theoretical representation, one can see the following relationships: | ||
| + | :$${\rm Pr}(A) \hspace{0.8cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$ | ||
| + | :$${\rm Pr}(B) \hspace{0.8cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$ | ||
| + | :$${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) + {\rm Pr}(\overline{A} \cap {B}).$$ | ||
| − | + | Adding the first two equations and subtracting from them the third, we get: | |
| − | $$\rm | + | :$${\rm Pr}(A) +{\rm Pr}(B) -{\rm Pr}(A \cup B) = {\rm Pr}(A \cap B).$$ |
| − | {{ | + | {{BlaueBox|TEXT= |
| − | + | $\text{Definition:}$ By rearranging this equation, one arrives at the so-called »'''addition rule'''« for any two, not necessarily disjoint events: | |
| − | {{ | + | :$${\rm Pr}(A \cup B) = {\rm Pr}(A) + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$}} |
| − | + | {{GraueBox|TEXT= | |
| − | $ | + | $\text{Example 7:}$ We consider again the experiment »throwing a die«. The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. |
| − | |||
| − | |||
| − | + | We consider the two sets | |
| + | * $A :=$ »The outcome is odd « $= \{1, 3, 5\}$ ⇒ ${\rm Pr}(A) = 3/6$, | ||
| + | |||
| + | * $B :=$ »The outcome is greater than $2$ « $ = \{3, 4, 5, 6\}$ ⇒ ${\rm Pr}(B) = 4/6$. | ||
| − | |||
| − | |||
| − | |||
| − | + | This gives the following probabilities | |
| − | $${\rm Pr}(X=1) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=\pi) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X={\rm e}) = 0.3 \hspace{0.05cm}.$$ | + | *of the union ⇒ ${\rm Pr}(A ∪ B) = 5/6$, and |
| − | + | ||
| − | + | *of the intersection ⇒ ${\rm Pr}(A ∩ B) = 2/6$. | |
| + | |||
| + | |||
| + | The numerical values show the validity of the addition rule: | ||
| + | :$$5/6 = 3/6 + 4/6 − 2/6.$$}} | ||
| + | |||
| + | ==Complete system== | ||
| + | <br> | ||
| + | In the last section to this chapter, we consider again more than two possible events, namely, in general, $I$. These events will be denoted by $A_i$ ⇒ the running index $i$ can be in the range $1 ≤ i ≤ I$. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ A constellation with events $A_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_i, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_I$ is called a »'''complete system'''«, if and only if the following two conditions are satisfied: | ||
| + | |||
| + | '''(1)''' All events are pairwise disjoint: | ||
| + | :$$A_i \cap A_j = \it \phi \hspace{0.25cm}\rm for\hspace{0.15cm}all\hspace{0.25cm}\it i \ne j.$$ | ||
| + | '''(2)''' The union of all event sets gives the universal set: | ||
| + | :$$\bigcup_{i=1}^{I} A_i = G.$$}} | ||
| + | |||
| + | |||
| + | Given these two assumptions, the sum of all probabilities is then: | ||
| + | :$$\sum_{i =1}^{ I} {\rm Pr}(A_i) = 1.$$ | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 8:}$ | ||
| + | *The sets $A_1 := \{1, 5\}$ and $A_2 := \{2, 3\}$ together with the set $A_3 := \{4, 6\}$ result in a complete system in the random experiment »throwing a die«, | ||
| + | |||
| + | * but not in the experiment »throwing a roulette ball«.}} | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 9:}$ Another example of a complete system is the discrete random variable $X = \{ x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ with the likelihood corresponding to the following [[Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables#Probability_mass_function_and_probability_density_function|»probability mass function«]] $\rm (PMF)$: | ||
| + | :$$P_X(X) = \big [ \hspace{0.1cm} P_X(x_1),\ P_X(x_2), \hspace{0.05cm}\text{...}\hspace{0.15cm},\ P_X(x_I) \hspace{0.05cm} \big ] = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_I \hspace{0.05cm} \big ] \hspace{0.05cm}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} p_1 = P_X(x_1) = {\rm Pr}(X=x_1) \hspace{0.05cm}, | ||
| + | \hspace{0.2cm}p_2 = {\rm Pr}(X=x_2) \hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.15cm},\hspace{0.2cm} p_I = {\rm Pr}(X=x_I) \hspace{0.05cm}.$$ | ||
| + | |||
| + | *The possible outcomes $x_i$ of the random variable $X$ are pairwise disjoint to each other. | ||
| + | |||
| + | *The sum of all likelihoods $p_1 + p_2 + \hspace{0.1cm}\text{...}\hspace{0.1cm} + \hspace{0.05cm} p_I$ always yields the result $1$.}} | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 10:}$ Let $X= \{0, 1, 2 \}$ and $P_X (X) = \big[0.2, \ 0.5, \ 0.3\big]$. Then holds: | ||
| + | :$${\rm Pr}(X=0) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=1) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=2) = 0.3 \hspace{0.05cm}.$$ | ||
| + | |||
| + | With random variable $X = \{1, \pi, {\rm e} \}$ and the same $P_X(X) = \big[0.2, \ 0.5, \ 0.3\big]$ the assignments are: | ||
| + | :$${\rm Pr}(X=1) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=\pi) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X={\rm e}) = 0.3 \hspace{0.05cm}.$$ | ||
| + | |||
| + | $\text{Hints:}$ | ||
| + | *The [[Information_Theory/Some_Preliminary_Remarks_on_Two-Dimensional_Random_Variables#Probability_mass_function_and_probability_density_function|»probability mass function«]] $P_X(X)$ only makes statements about probabilities, not about the set of values $\{x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ of the random variable $X$. | ||
| + | |||
| + | *This additional information is provided by the [[Theory_of_Stochastic_Signals/Probability_Density_Function_(PDF)#Definition_of_the_probability_density_function|»probability density function«]] $\rm (PDF)$.}} | ||
| + | |||
| + | ==Exercises for the chapter== | ||
| + | <br> | ||
| + | [[Aufgaben:Exercise_1.2:_Switching_Logic_(D/B_Converter)|Exercise 1.2: Switching Logic (D/B Converter)]] | ||
| + | |||
| + | [[Aufgaben:Exercise_1.2Z:_Sets_of_Digits|Exercise 1.2Z: Sets of Digits]] | ||
| + | |||
| + | [[Aufgaben:Exercise_1.3:_Fictional_University_Somewhere|Exercise 1.3: Fictional University Somewhere]] | ||
| + | |||
| + | [[Aufgaben:Exercise_1.3Z:_Winning_with_Roulette%3F|Exercise 1.3Z: Winning with Roulette?]] | ||
| + | |||
{{Display}} | {{Display}} | ||
Latest revision as of 16:41, 5 February 2024
Contents
Venn diagram, universal and empty set
In later chapters, we will sometimes refer to »set theory« . Therefore, the most important basics and definitions of this discipline will be briefly summarized here. The topic is also covered in the $($German language$)$ learning video »Mengentheoretische Begriffe und Gesetzmäßigkeiten« ⇒ »Set Theory – Terms and Regularities«.
An important tool of set theory is the »Venn diagram« according to the graph:
- Applied to probability theory, the events $A_i$ are represented here as areas. For a simpler description we do not denote the events here with $A_1$, $A_2$ and $A_3$, but with $A$, $B$ and $C$ in contrast to the last chapter.
- The total area corresponds to the »universal set« $($or short: »universe«$)$ $G$. The universe $G$ contains all possible outcomes and stands for the »certain event«, which by definition occurs with probability »one«: ${\rm Pr}(G) = 1$. For example, in the random experiment »Throwing a die«, the probability for the event »The number of eyes is less than or equal to 6« is identical to one.
- In contrast, the »empty set« $ϕ$ does not contain a single element. In terms of events, the empty set specifies the »impossible event« with probability ${\rm Pr}(ϕ) = 0$ an. For example, in the experiment »Throwing a die«, the probability for the event »The number of eyes is greater than 6« is identically zero.
It should be noted that not every event $A$ with ${\rm Pr}(A) = 0$ can really never occur:
- Thus, the probability of the event »the noise value $n$ is identical to zero» is vanishingly small and it applies ${\rm Pr}(n \equiv 0) = 0$, if $n$ is described by a continuous–valued $($Gaussian$)$ random variable.
- Nevertheless, it is of course possible $($although extremely unlikely$)$ that at some points the exact noise value $n = 0$ will also occur.
Union set
Some set-theoretical relations are explained now on the basis of the Venn diagram.
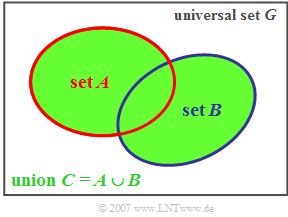
$\text{Definition:}$ The »union set« $C$ of two sets $A$ and $B$ contains all the elements that are contained either in set $A$ or in set $B$ or in both.
- This relationship is expressed as the following formula:
- $$\ C = A \cup B.$$
- Using the diagram, it is easy to see the following laws of set theory:
- $$A \cup \it \phi = A \rm \hspace{3.6cm}(union \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}empty \hspace{0.15cm}set),$$
- $$A\cup G = G \rm \hspace{3.6cm}(union \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}universe),$$
- $$A\cup A = A \hspace{3.6cm}(\rm tautology),$$
- $$A\cup B = B\cup A \hspace{2.75cm}(\rm commutative \hspace{0.15cm}property),$$
- $$(A\cup B)\cup C = A\cup (B\cup C) \hspace{0.45cm}(\rm associative \hspace{0.15cm}property).$$
- If nothing else is known about the event sets $A$ and $B$ then only a lower bound and an upper bound can be given for the probability of the union set:
- $${\rm Max}\big({\rm Pr} (A), \ {\rm Pr} (B)\big) \le {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B).$$
- The probability of the union set is equal to the lower bound if $A$ is a $\text{subset}$ of $B$ or vice versa.
- The upper bound holds for »disjoint sets«.
$\text{Example 1:}$ We consider again the experiment »throwing a die«. The possible outcomes $($number of points$)$ are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Consider the two events
- $A :=$ »The outcome is greater than or equal to $5$ « $ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$,
- $B :=$ »The outcome is even « $= \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$,
then the union set contains four elements: $(A \cup B) = \{2, 4, 5, 6 \}$ ⇒ ${\rm Pr} (A \cup B) = 4/6 = 2/3$.
- For the lower bound: ${\rm Pr} (A \cup B) \ge {\rm Max}\big({\rm Pr} (A),\ {\rm Pr} (B)\big ) = 3/6.$
- For the upper bound: $ {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B) = 5/6.$
Intersection set
Another important set-theoretic relation is the intersection.
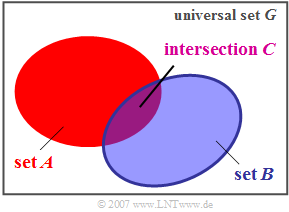
$\text{Definition:}$ The »intersection set« $C$ of two sets $A$ and $B$ contains all those elements which are contained in both the set $A$ and the set $B$.
- This relationship is expressed as the following formula:
- $$C = A \cap B.$$
- In the diagram, the intersection is shown in purple. Analog to the union set, the following regularities apply here:
- $$A \cap \it \phi = \it \phi \rm \hspace{3.75cm}(intersection \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}empty \hspace{0.15cm}set),$$
- $$A \cap G = A \rm \hspace{3.6cm}(intersection \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}universe),$$
- $$A\cap A = A \rm \hspace{3.6cm}(tautology),$$
- $$A\cap B = B\cap A \rm \hspace{2.75cm}(commutative \hspace{0.15cm}property),$$
- $$(A\cap B)\cap C = A\cap (B\cap C) \rm \hspace{0.45cm}(associative \hspace{0.15cm}property).$$
- If nothing else is known about $A$ and $B$, then no statement can be made for the probability of the intersection.
- However, if ${\rm Pr} (A) \le 1/2$ and at the same time ${\rm Pr} (B) \le 1/2$ hold, then a lower and an upper bound can be given:
- $$0 \le {\rm Pr} (A ∩ B) \le {\rm Min}\ \big({\rm Pr} (A),\ {\rm Pr} (B)\big ).$$
- ${\rm Pr}(A ∩ B)$ is sometimes called the »joint probability« and is denoted by ${\rm Pr}(A, \ B)$.
- ${\rm Pr}(A ∩ B)$ is equal to the upper bound if $A$ is a $\text{subset}$ of $B$ or vice versa.
- The lower bound is obtained for the joint probability of »disjoint sets«.
$\text{Example 2:}$ We consider again the experiment »throwing a die«. The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Consider the two events
- $A :=$ »The outcome is greater than or equal to $5$« $ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$,
- $B :=$ »The outcome is even« $ = \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$.
The intersection contains only one element: $(A ∩ B) = \{ 6 \}$ ⇒ ${\rm Pr} (A ∩ B) = 1/6$.
- The upper bound is obtained as ${\rm Pr} (A ∩ B) \le {\rm Min}\ \big ({\rm Pr} (A), \, {\rm Pr} (B)\big ) = 2/6.$
- The lower bound of the intersection is zero because of ${\rm Pr} (A) \le 1/2$ and ${\rm Pr} (B) \le 1/2$ .
Complementary set
$\text{Definition:}$ The »complementary set« of $A$ is often denoted by a straight line above the letter $(\overline{A})$ . It contains all the elements that are not contained in the set $A$ and it holds for their probability:
- $${\rm Pr}(\overline{A}) = 1- {\rm Pr}(A).$$
In the Venn diagram, the set complementary to $A$ is shaded.
From this diagram, some set-theoretic relationships can be seen:
- The complementary of the complementary of $A$ is the set $A$ itself:
- $$\overline{\overline{A} } = A.$$
- The union of a set $A$ with its complementary set gives the universal set:
- $${\rm Pr}(A \cup \overline{A}) = {\rm Pr}(G) = \rm 1.$$
- The intersection of $A$ with its complementary set gives the empty set:
- $${\rm Pr}(A \cap \overline{A}) = {\rm Pr}({\it \phi}) \rm = 0.$$
$\text{Example 3:}$ We consider again the experiment »throwing a die». The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
- Starting from the set
- $$A :=\text{ »The outcome is smaller than $5$« } = \{1, 2, 3, 4\}\ \ \text{ ⇒ } \ \ {\rm Pr} (A)= 2/3,$$
- the corresponding complementary set is
- $$\overline{A} :=\text{ »The outcome is greater than or equal to $5$«} = \{5, 6\} \ \ \text{ ⇒ }\ \ {\rm Pr} (\overline{A})= 1 - {\rm Pr} (A) = 1 - 2/3 = 1/3.$$
Proper subset – Improper subset
$\text{Definitions:}$
(1) One calls $A$ a »proper subset« of $B$ and writes for this relationship $A ⊂ B$,
- if all elements of $A$ are also contained in $B$,
- but not all elements of $B$ are contained in $A$.
In this case, for the probabilities hold:
- $${\rm Pr}(A) < {\rm Pr}(B).$$
This set-theoretic relationship is illustrated by the sketched Venn diagram on the right.
(2) On the other hand, $A$ is called an »improper subset« of $B$ and uses the notation
- $$A \subseteq B = (A \subset B) \cup (A = B),$$
if $A$ is either a proper subset of $B$ or if $A$ and $B$ are equal sets.
- Then applies to the probabilities: ${\rm Pr} (A) \le {\rm Pr} (B)$.
- The equality sign is only valid for the special case $A = B$.
In addition, the two equations known as the »absorption laws« also apply:
- $$(A \cap B) \cup A = A ,$$
- $$(A \cup B) \cap A = A,$$
- since the intersection $A ∩ B$ is always a subset of $A$,
- but at the same time $A$ is also a subset of the union $A ∪ B$.
$\text{Example 4:}$ We consider again the experiment »throwing a die«. The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Consider the two events
- $A :=$ »The outcome is odd« $ = \{1, 3, 5\}$ ⇒ ${\rm Pr} (A)= 3/6$,
- $B :=$ »The outcome is a prime number» $ = \{1, 2, 3, 5\}$ ⇒ ${\rm Pr} (B)= 4/6$.
It can be seen that $A$ is a $($proper$)$ subset of $B$. Accordingly, ${\rm Pr} (A) < {\rm Pr} (B)$ is also true.
Theorems of de Morgan
In many set-theoretical tasks, the two theorems of $\text{de Morgan}$ are extremely useful.
$\text{Theorem of de Morgan:}$
- $$\overline{A \cup B} = \overline{A} \cap \overline{B},$$
- $$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$
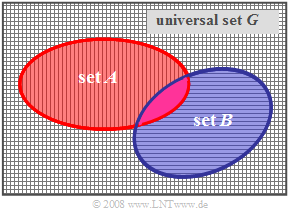
These regularities are illustrated in the Venn diagram:
- Set $A$ is shown in red and set $B$ is shown in blue.
- The complement $\overline {A}$ of $A$ is hatched in the horizontal direction.
- The complement $\overline {B}$ of $B$ is hatched in the vertical direction.
- The complement $\overline{A \cup B}$ of the union ${A \cup B}$ is hatched both horizontally and vertically.
- It is thus equal to the intersection $\overline{A} \cap \overline{B}$ of the two complement sets of $A$ and $B$:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B}.$$
The second form of the de Morgan theorem can also be illustrated graphically with the same Venn diagram:
- The intersection $A ∩ B$ $($shown in purple in the figure$)$ is neither horizontally nor vertically hatched.
- Accordingly, the complement $\overline{A ∩ B}$ of the intersection is hatched either horizontally, vertically, or in both directions.
- By de Morgan's second theorem, the complement of the intersection equals the union of the two complementary sets of $A$ and $B$:
- $$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$
$\text{Example 5:}$ We consider again the experiment »throwing a die«. The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
We consider the two sets
- $A : =$ »The outcome is odd« $= \{1, 3, 5\}$,
- $B : =$ »The outcome is greater than $2$« $= \{3, 4, 5, 6\}$.
From this follow the two complementary sets
- $\overline {A} : =$ »The outcome is even« $= \{2, 4, 6\}$,
- $\overline {B} : =$ »The outcome is smaller than $3$« $= \{1, 2\}$.
Further, using the above theorems, we obtain the following sets:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B} = \{2\},$$
- $$\overline{\it A \cap \it B} =\overline{\it A} \cup \overline{\it B} = \{1,2,4,6\}.$$
Disjoint sets
$\text{Definition:}$ Two sets $A$ and $B$ are called »disjoint« or »incompatible«,
- if there is no single element,
- that is contained in both $A$ and $B$.
The diagram shows two disjoint sets $A$ and $B$ in the Venn diagram.
In this special case, the following statements hold:
- The intersection of two disjoint sets $A$ and $B$ always yields the empty set:
- $${\rm Pr}(A \cap B) = {\rm Pr}(\phi) = \rm 0.$$
- The probability of the union set of two disjoint sets $A$ and $B$ is always equal to the sum of the two individual probabilities:
- $${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B).$$
$\text{Example 6:}$ We consider again the experiment »throwing a die«. The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
In our standard experiment, the two sets are now
- $A :=$ »The outcome is smaller than $3$ « $ = \{1, 2\}$ ⇒ ${\rm Pr}( A) = 2/6$,
- $B :=$ »The outcome is greater than $3$ « $ = \{4, 5,6\}$ ⇒ ${\rm Pr}( B) = 3/6$
disjoint to each other, since $A$ and $B$ do not contain a single common element.
- The intersection yields the empty set: ${A \cap B} = \phi$.
- The probability of the union set ${A \cup B} = \{1, 2, 4, 5, 6\}$ is equal to ${\rm Pr}( A) + {\rm Pr}(B) = 5/6.$
Addition rule
Only for disjoint sets $A$ and $B$, the relation ${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B)$ holds for the probability of the union set. But how is this probability calculated for general events that are not necessarily disjoint?
Consider the right-hand Venn diagram with the intersection $A ∩ B$ shown in purple:
- The red set contains all the elements that belong to $A$, but not to $B$.
- The elements of $B$, that are not simultaneously contained in $A$ are shown in blue.
- All red, blue, and purple surfaces together make up the union set $A ∪ B$.
From this set-theoretical representation, one can see the following relationships:
- $${\rm Pr}(A) \hspace{0.8cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$
- $${\rm Pr}(B) \hspace{0.8cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$
- $${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) + {\rm Pr}(\overline{A} \cap {B}).$$
Adding the first two equations and subtracting from them the third, we get:
- $${\rm Pr}(A) +{\rm Pr}(B) -{\rm Pr}(A \cup B) = {\rm Pr}(A \cap B).$$
$\text{Definition:}$ By rearranging this equation, one arrives at the so-called »addition rule« for any two, not necessarily disjoint events:
- $${\rm Pr}(A \cup B) = {\rm Pr}(A) + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$
$\text{Example 7:}$ We consider again the experiment »throwing a die«. The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
We consider the two sets
- $A :=$ »The outcome is odd « $= \{1, 3, 5\}$ ⇒ ${\rm Pr}(A) = 3/6$,
- $B :=$ »The outcome is greater than $2$ « $ = \{3, 4, 5, 6\}$ ⇒ ${\rm Pr}(B) = 4/6$.
This gives the following probabilities
- of the union ⇒ ${\rm Pr}(A ∪ B) = 5/6$, and
- of the intersection ⇒ ${\rm Pr}(A ∩ B) = 2/6$.
The numerical values show the validity of the addition rule:
- $$5/6 = 3/6 + 4/6 − 2/6.$$
Complete system
In the last section to this chapter, we consider again more than two possible events, namely, in general, $I$. These events will be denoted by $A_i$ ⇒ the running index $i$ can be in the range $1 ≤ i ≤ I$.
$\text{Definition:}$ A constellation with events $A_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_i, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_I$ is called a »complete system«, if and only if the following two conditions are satisfied:
(1) All events are pairwise disjoint:
- $$A_i \cap A_j = \it \phi \hspace{0.25cm}\rm for\hspace{0.15cm}all\hspace{0.25cm}\it i \ne j.$$
(2) The union of all event sets gives the universal set:
- $$\bigcup_{i=1}^{I} A_i = G.$$
Given these two assumptions, the sum of all probabilities is then:
- $$\sum_{i =1}^{ I} {\rm Pr}(A_i) = 1.$$
$\text{Example 8:}$
- The sets $A_1 := \{1, 5\}$ and $A_2 := \{2, 3\}$ together with the set $A_3 := \{4, 6\}$ result in a complete system in the random experiment »throwing a die«,
- but not in the experiment »throwing a roulette ball«.
$\text{Example 9:}$ Another example of a complete system is the discrete random variable $X = \{ x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ with the likelihood corresponding to the following »probability mass function« $\rm (PMF)$:
- $$P_X(X) = \big [ \hspace{0.1cm} P_X(x_1),\ P_X(x_2), \hspace{0.05cm}\text{...}\hspace{0.15cm},\ P_X(x_I) \hspace{0.05cm} \big ] = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_I \hspace{0.05cm} \big ] \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} p_1 = P_X(x_1) = {\rm Pr}(X=x_1) \hspace{0.05cm}, \hspace{0.2cm}p_2 = {\rm Pr}(X=x_2) \hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.15cm},\hspace{0.2cm} p_I = {\rm Pr}(X=x_I) \hspace{0.05cm}.$$
- The possible outcomes $x_i$ of the random variable $X$ are pairwise disjoint to each other.
- The sum of all likelihoods $p_1 + p_2 + \hspace{0.1cm}\text{...}\hspace{0.1cm} + \hspace{0.05cm} p_I$ always yields the result $1$.
$\text{Example 10:}$ Let $X= \{0, 1, 2 \}$ and $P_X (X) = \big[0.2, \ 0.5, \ 0.3\big]$. Then holds:
- $${\rm Pr}(X=0) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=1) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=2) = 0.3 \hspace{0.05cm}.$$
With random variable $X = \{1, \pi, {\rm e} \}$ and the same $P_X(X) = \big[0.2, \ 0.5, \ 0.3\big]$ the assignments are:
- $${\rm Pr}(X=1) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=\pi) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X={\rm e}) = 0.3 \hspace{0.05cm}.$$
$\text{Hints:}$
- The »probability mass function« $P_X(X)$ only makes statements about probabilities, not about the set of values $\{x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ of the random variable $X$.
- This additional information is provided by the »probability density function« $\rm (PDF)$.
Exercises for the chapter
Exercise 1.2: Switching Logic (D/B Converter)
Exercise 1.3: Fictional University Somewhere
Exercise 1.3Z: Winning with Roulette?