Exercise 1.08Z: BPSK Error Probability

• Return to book

Numerical values of function  ${\rm Q}(x)$

We assume the optimal baseband transmission system for binary signals with

• bipolar amplitude coefficients  $a_{\nu} \in \{–1, +1\}$,

• rectangular transmitted signal with signal values  $\pm s_{0}$  and bit duration  $T_{\rm B}$,

• AWGN noise with noise power density  $N_{0}$,

• receiver filter according to the matched filter principle,

• decision with the optimal threshold  $E = 0$.

Unless otherwise specified,  you should also assume the following numerical values:

$$s_0 = 4\,{\rm V},\hspace{0.2cm} T_{\rm B} = 1\,{\rm ns},\hspace{0.2cm}N_0 = 2 \cdot 10^{-9}\, {\rm V^2/Hz} \hspace{0.05cm}.$$

The bit error probability of this  "baseband system"  has already been given in the chapter  "Error Probability for Baseband Transmission"  $($Index:  $\rm BB)$:

$$p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}.$$

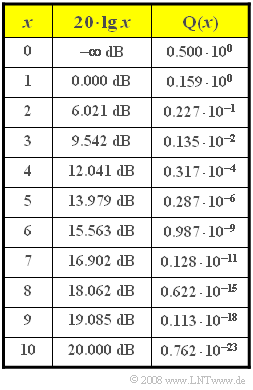
Here,  $\sigma_{d}$  denotes the noise rms value at the decision device and  ${\rm Q}(x)$  denotes the complementary Gaussian error function,  which is given here in tabular form.  This error probability can also be expressed in the form

$$p_{\rm BB} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ),$$

where  $E_{\rm B}$  denotes  "energy per bit."

The error probability of a comparable transmission system with  "Binary Phase Shift Keying" is  $($Index:  $\rm BPSK)$:

$$p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )\hspace{0.2cm}{\rm with}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/{T_{\rm B}}}.$$

Notes:

• The exercise belongs to the chapter  "Linear Digital Modulation - Coherent Demodulation".

• Reference is also made to the chapter  "Error Probability for Baseband Transmission".

• You can check the results with the HTML5/JavaScript applet  "Complementary Gaussian Error Functions".

• Since the signal value  $s_{0}$  is specified here in  "volts"  and no specification is made for the reference resistance,  $E_{\rm B}$  has the unit "$\rm V^{2}/Hz$".

Questions

1

Let  $s_{0} = 4 \, \rm V$.  What is the error probability  $p_{\rm BB}$  of the baseband system?

$p_{\rm BB} \ = \ $ $\ \%$

2

What is the energy per bit for the baseband system with  $s_{0} = 4 \, \rm V$?

$E_{\rm B} \ = \ $ $\ \cdot 10^{-8}\ \rm V^{2}s$

3

What is the error probability  $p_{\rm BB}$  at half the transmission amplitude   $(s_{0} = 2 \, \rm V)$?

$p_{\rm BB} \ = \ $ $\ \%$

4

Give the error probability of the BPSK depending on the quotient  $E_{\rm B}/N_{0}$.  Which result is correct?

	$p_{\rm BPSK} = {\rm Q}\big [(E_{\rm B}/N_{0})^{1/2}\big ]$,
	$p_{\rm BPSK} = {\rm Q}\big [(2 \cdot E_{\rm B}/N_{0})^{1/2}\big ]$,
	$p_{\rm BPSK} = {\rm Q}\big [(4\cdot E_{\rm B}/N_{0})^{1/2}\big ]$.

5

What are the error probabilities for the BPSK and  $E_{\rm B}/N_{0} = 8$  resp.  $E_{\rm B}/N_{0} = 2$?

$E_{\rm B}/N_{0} = 8\text{:}\hspace{0.4cm} p_{\rm BPSK} \ = \ $ $\ \%$

$E_{\rm B}/N_{0} = 2\text{:}\hspace{0.4cm} p_{\rm BPSK} \ = \ $ $\ \%$

Solution

Solution

(1)  The noise rms value is given here by

$$\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}= \sqrt{\frac{2 \cdot 10^{-9}\,{\rm V^2/Hz}}{2 \cdot 1\,{\rm ns}}}= 1\,{\rm V}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}p_{\rm BB} = {\rm Q}\left ({s_0}/{\sigma_d } \right )= {\rm Q}(4)= 0.317 \cdot 10^{-4}\hspace{0.1cm}\underline {= 0.00317 \%}.$$

(2)  For the baseband system:

$$E_{\rm B} = s_0^2 \cdot T_{\rm B}= (4\,{\rm V})^2 \cdot 10^{-9}\,{\rm s}\hspace{0.1cm}\underline {= 1.6 \cdot 10^{-8}\,{\rm V^2s}}.$$

• Of course, the additional given equation gives the exact same error probability:

$$p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 16 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(4)= 0.317 \cdot 10^{-4}.$$

• A comparison with question  (4)  of  "Exercise 1.8"  shows that  $E_{\rm B}/N_{0} = 8$  is not  (exactly)  equal to  $10 \cdot \lg E_{\rm B}/N_{0} = 9 \ \rm dB$. 
• In the first case  $p_{\rm BB} = 0.317 \cdot 10^{–4}$ is obtained,  in the second  $p_{\rm BB} = 0.336 \cdot 10^{-4}$.

(3)  At half the transmission amplitude  $s_{0} = 2 \ \rm V$,  the energy per bit decreases to a quarter and the following equations apply:

$$p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{\sigma_d } \right )= {\rm Q}\left ( \frac{2\,{\rm V}}{1\,{\rm V}} \right )\hspace{0.1cm}\underline {= {\rm Q}(2)= 2.27 \%},$$

$$p_{\rm BB} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{\frac{2 \cdot 4 \cdot 10^{-9}\,{\rm V^2s}}{2 \cdot 10^{-9}\, {\rm V^2/Hz} }} \hspace{0.1cm}\right ) = {\rm Q}(2)= 2.27 \%.$$

(4)  Considering only half the energy  $E_{\rm B} = s^{2}_{0} \cdot T_{\rm B}/2$,  we obtain with  $\sigma^{2}_{d} = N_{0}/T_{\rm B}$  and

$$p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{\sigma_d } \right )= {\rm Q}\left ( \sqrt{{s_0^2 \cdot T_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }}\hspace{0.1cm}\right )$$

the exact same result as for the optimal baseband system   ⇒   solution 2.

(5)  Of course,  this also gives the exact same results as for the baseband transmission:

$${ E_{\rm B}}/{N_0 }= 8{\rm :} \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{16}) = {\rm Q}(4)\hspace{0.1cm}\underline {= 0.00317 \%},$$

$${ E_{\rm B}}/{N_0 }= 2{\rm :} \hspace{0.2cm}p_{\rm BPSK} = {\rm Q}(\sqrt{4}) = {\rm Q}(2) \hspace{0.1cm}\underline {= 2.27 \%}.$$