Exercise 1.4: AMI and MMS43 Code

Modified AMI code and MMS43 code

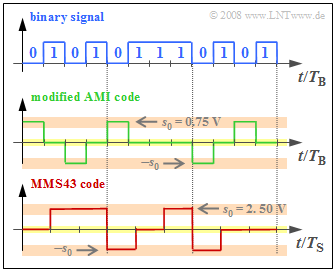
Two different ternary transmission codes are used with ISDN, which are to be clarified in the diagram at an exemplary binary input signal.

The upper diagram shows twelve bits $($each with bit duration $T_{\rm B})$.

On the $\rm S_{0}$ interface $($between NTBA and terminal equipment$)$, the $\text{modified AMI code}$ is used. The difference to the conventional AMI code is the swapping $0 \Leftrightarrow 1$ of the binary input signal.

In contrast, the $\text{MMS43 code}$ $($Modified Monitoring Sum 4B3T$)$ is used on the $\rm U_{K0}$ interface, where four binary symbols are replaced by three ternary symbols $($voltage values $0 \ {\rm V}, +2.5 \ {\rm V}$ and $-2.5 \ {\rm V})$. The assignment is done depending on the previously coded symbols.

Notes:

The exercise belongs to the chapter "ISDN Basic Access".

Information on the MMS43 code can be found in the chapter "Block Coding with 4B3T Codes" of the book "Digital Signal Transmission".

Information on the AMI code can be found in the chapter "Symbolwise Coding with Pseudo-Ternary Codes" of the same book.

Questions

	Symbol duration $T_{\rm S}$ and bit duration $T_{\rm B}$ of the binary signal are the same.
	The encoding is done symbol-by-symbol.
	Each binary "0" is represented by $0 \hspace{0.1cm} \rm V$.
	The binary "1" is alternately represented by $+s_{0}$ and $-s_{0}$.

$r_{\rm AMI} \ = \ $

$\ \%$

$P_{\rm S, \ AMI} \ = \ $

$\ \rm mW$

	Symbol duration $T_{\rm S}$ and bit duration $T_{\rm B}$ of the binary signal are the same.
	The encoding is done block-by-block.
	Each binary "0" is represented by $0 \hspace{0.1cm} \rm V$.

$r_{\rm MMS43} \ = \ $

$\ \%$

$R_{\rm U_{K0}} \ = \ $

$\ \rm ternary \ symbols/second$

$P_{\rm S,\ MMS43} \ = \ $

$\ \rm mW$

Solution

(1) The first two statements are correct:

The modified AMI code is a pseudo-ternary code with $T_{\rm S} = T_{\rm B}$ and symbol-wise coding. The stated assignments apply to the conventional AMI code.

On the other hand, in the modified AMI code the binary "1" is represented by the voltage value $0 \ \rm V$ and the binary "0" alternately by $+s_{0}$ resp. $-s_{0}$, where for $s_{0} = 0.75 \ \rm V$ is to be set.

(2) The equivalent bit rate of the AMI encoded signal is $R_{\rm C} = {\rm log_2}\hspace{0.05cm}(3)/T_{\rm S}$.

The bit rate of the redundancy-free binary source signal is equal to $R_{\rm B} = 1/T_{\rm B}$.

With $T_{\rm S} = T_{\rm B}$, according to the chapter "Basics of Coded Transmission" of the book "Digital Signal Transmission", we obtain for the (relative) redundancy of the modified AMI code:

$$r_{\rm AMI} = \frac{R_{\rm C}-R_{\rm B}}{R_{\rm C}} = 1 - \frac{1}{{\rm ld}\,(3)} \hspace{0.15cm}\underline{\approx 36.9\,\%} \hspace{0.05cm}.$$

(3) Using the unit impedance $R = 1 \ \rm \Omega $, the following applies to the transmit power $($with the unit $\rm V^{2})$:

$$P_{\rm S,\,AMI} = {1}/{2} \cdot {s_0}^2 = {1}/{2} \cdot {0.75\,{\rm V}}^2 \approx 0.28\,{\rm V^2} \hspace{0.05cm}.$$

Here it is considered that the AMI encoded signal is equal to $0 \ \rm V$ in half of the time.

Finally, considering the impedance $R = 100 \ \rm \Omega$, we get:

$$P_{\rm S,\,AMI} = \frac{0.28\,{\rm V^2}}{100\,\Omega} \hspace{0.15cm}\underline{ = 2.8\,{\rm mW}} \hspace{0.05cm}.$$

(4) The MMS43 code actually operates in blocks, with $m_{q} = 4$ binary symbols replaced by $m_{c} = 3 $ ternary symbols:

$$4 \cdot T_{\rm B} = 3 \cdot T_{\rm S}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm S} = {4}/{3} \cdot T_{\rm B} \hspace{0.05cm}.$$

That means: The first solution does not apply as well as the last one. Only solution 2 is correct:

In block coding, the binary symbol "0" cannot be uniformly replaced by the same code symbol. Rather, the encoding can be described as follows, assuming the running digital sum ${\it \Sigma}_{0} = 0$ at the beginning $($see graphic in the information section$)$:

$$\mathbf{0 1 0 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{0 + +}\hspace{0.2cm}({\it \Sigma}_1 = 2)\hspace{0.05cm},$$

$$ \mathbf{0 1 1 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{- \,0 \,\,+}\hspace{0.2cm}({\it \Sigma}_2 = 2)\hspace{0.05cm},$$

$$ \mathbf{0 1 0 1} \hspace{0.1cm} \ \Rightarrow \ \hspace{0.1cm}\mathbf{- \,0\,\,\, 0}\hspace{0.2cm}({\it \Sigma}_3 = 1) \hspace{0.05cm}.$$

"Exercise 1.4Z" discusses the MMS43 code in more detail.

(5) The MMS43 code belongs to the class of 4B3T codes. For these it is valid:

$$R_{\rm B} = \frac{1}{T_{\rm B}}, \hspace{0.2cm} R_{\rm C} = \frac{{\rm ld}\,(3)}{T_{\rm S}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}r_{\rm MMS43} = 1 - \frac{R_{\rm B}}{R_{\rm C}} = 1 - \frac{T_{\rm S}/T_{\rm B}}{{\rm ld}\,(3)} = 1 - \frac{4/3}{{\rm log_2}\,(3)} \hspace{0.15cm}\underline{\approx 15.9\,\%} \hspace{0.05cm}.$$

(6) The following number of ternary symbols are transmitted on the $\rm U_{K0}$ bus per millisecond:

Channel B1: $64$ binary symbols ⇒ $48$ ternary symbols,
Channel B2: $64$ binary symbols ⇒ $48$ ternary symbols,
D channel: $16$ binary symbols ⇒ $12$ ternary symbols,
Synchronization and control symbols ⇒ $12$ ternary symbols.

As a sum, this results in $120$ ternary symbols per millisecond or $\underline{120,000}$ ternary symbols per second.

(7) Considering the note in the information section and the larger transmission amplitude $s_{0} = 2.5 \ \rm V$ compared to the (modified) AMI code, we obtain:

$$P_{\rm S,\,MMS43} = \frac{2}{3} \cdot \frac{{s_0}^2}{R} = \frac{2}{3} \cdot \frac{({2.5\,{\rm V}})^2}{100\,{\rm \Omega}} \hspace{0.15cm}\underline{\approx 4.2\,{\rm mW}} \hspace{0.05cm}.$$