Exercise 1.4Z: Complex Nyquist Spectrum
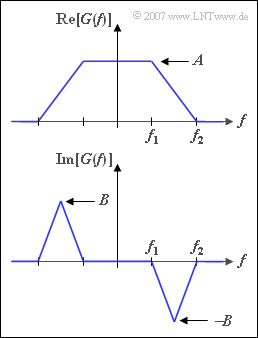
Consider a pulse $g(t)$ with spectrum $G(f)$ according to the sketch. One recognizes from this representation:
- The real part of $G(f)$ is trapezoidal with the corner frequencies $f_{1} = 3 \, \rm kHz$ and $f_{2} = 7 \, \rm kHz$. In the range $|f| < f_{1}$:
- $${\rm Re}\big[G(f)\big] = A = 10^{-4} \, \rm V/Hz.$$
- The imaginary part of $G(f)$ is always assumed to be ${\rm Im}\big[G(f)\big] =0$ for subtasks (1) to (5). In this case $g(t)$ is certainly a Nyquist pulse.
- From subtask (6), the imaginary part ${\rm Im}[G(f)]$ in the range $f_{1} \leq | f | \leq f_{2}$ has a triangular shape with the values $\pm B$ at the triangle peaks.
It is necessary to check whether the pulse $g(t)$ satisfies the first Nyquist condition even with complex spectrum:
- $$g(\nu T) = \left\{ \begin{array}{c} g_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} \nu = 0 \hspace{0.05cm}, \\ \nu \ne 0 \hspace{0.1cm}. \\ \end{array}$$
In the course of this exercise, reference is made to the following descriptive quantities:
- The Nyquist frequency gives the symmetry point of the rolloff:
- $$f_{\rm Nyq}= \frac{1}{2T}= \frac{f_1 +f_2 } {2 }\hspace{0.05cm}.$$
- The rolloff factor is a measure of the transition steepness:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Properties of Nyquist Systems".
- The inverse Fourier transform $g(t)$ of a trapezoidal Nyquist spectrum with rolloff factor $r$ can be assumed to be known:
- $$g ( t )= g_0 \cdot {\rm sinc} \left ( { t}/{T}\right)\cdot {\rm sinc} \left ( { r \cdot t}/{T}\right),\hspace{0.3cm} {\rm sinc}(x)= \sin(\pi \cdot x)/(\pi \cdot x).$$
- A triangular low–pass spectrum $G(f)$ limited to $| f | < f_{0}$ and where $G(f = 0) = B$, after inverse Fourier transform, leads to the time function
- $$g ( t )= B \cdot f_0 \cdot {\rm sinc}^2 \left ( { f_0 \cdot t}\right)\hspace{0.05cm},\hspace{0.3cm} {\rm sinc}(x)= \sin(\pi \cdot x)/(\pi \cdot x).$$
Questions
Solution
- $$f_{\rm Nyq}= \frac{f_1 +f_2 } {2 }= \frac{3\, {\rm kHz} + 7\, {\rm kHz}} {2 } \hspace{0.1cm}\underline { = 5\, {\rm kHz}} \hspace{0.05cm}.$$
(2) The rolloff factor is also determined by the two corner frequencies $f_{1}$ and $f_{2}$:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } = \frac{7\, {\rm kHz} - 3\, {\rm kHz}} {7\, {\rm kHz} + 3\, {\rm kHz} }\hspace{0.1cm}\underline { = 0.4 }\hspace{0.05cm}.$$
(3) For a pulse with real low–pass spectrum, the maximum is always at $t = 0$ and it holds:
- $$g_0 = g(t=0) = \int_{-\infty}^{+\infty}G(f) \,{\rm d} f = A \cdot 2 f_{\rm Nyq} = 10^{-4 }\,\frac{\rm V}{\rm Hz}\cdot 2 \cdot 5 \cdot10^{3} \,{\rm Hz}\hspace{0.1cm}\underline { = 1\,{\rm V}}\hspace{0.05cm}.$$
(4) For the Nyquist pulse, the equidistant zero crossings occur at the interval $T = 1/(2f_{\rm Nyq}) = 100 \, \rm µ s$. From this one obtains directly:
- $$g(t= 100\,{\rm µ s}) = \ \hspace{0.1cm}\underline { g(T) = 0,}$$
- $$g(t= 200\,{\rm µ s}) = \ \hspace{0.1cm}\underline {g(2T) = 0} \hspace{0.05cm}.$$
This result also follows from the given equation with $r = 0.4$:
- $$g ( t )= g_0 \cdot {\rm sinc} \left ( { t}/{T}\right)\cdot {\rm sinc} \left ( {0.4 \cdot t}/{T}\right) \hspace{0.05cm}.$$
Responsible for satisfying the first Nyquist condition is the first term.
(5) According to the equation given in (4):
- $$g(t= 250\,{\rm µ s})= g_0 \cdot {\rm sinc} ( {1 })\cdot {\rm sinc} ( 2.5 )\hspace{0.1cm}\underline { = 0} \hspace{0.05cm}.$$
This zero is due to the second term and does not lie in the Nyquist time grid $\nu T$
(6) For the following derivation, let $g(t)= g_{\rm R}(t) + g_{\rm I}(t) \hspace{0.05cm},$ where $g_{\rm R}(t)$ is due to the real part and $g_{\rm I}(t)$ is due to the imaginary part of $G(f)$.
- The first part is calculated exactly as in point (4):
- $$g_{\rm R} ( t )= g_0 \cdot {\rm sinc} \left ( { t}/{T}\right)\cdot {\rm sinc} \left ( { 0.4 \cdot t}/{T}\right) \hspace{0.05cm}.$$
- To satisfy the first Nyquist criterion, the following must hold for the imaginary part with $1/T = 10 \, \rm kHz$:
- $$\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G \left ( f - {k}/{T} \right)\right]= 0 \hspace{0.05cm}.$$
- With the given corner frequencies $f_{1} = 3 \, \rm kHz$ and $f_{2} = 7 \ \rm kHz$, the two triangles are around $\pm 5\, \rm kHz$, so the above equation is satisfied.
- The same is true for $f_{1} = 4.5\, \rm kHz$ and $f_{2} = 5.5 \, \rm kHz$.
- In contrast, the triangle peaks with $f_{1} = 3\, \rm kHz$ and $f_{2} = 5 \, \rm kHz$ are at $\pm 4 \ \rm kHz$.
- In this case the triangle functions do not cancel due to the periodic continuation and the Nyquist condition is not fulfilled.
Therefore the correct solutions are 1 and 3.
(7) With the result $g_{\rm R}(2.5T) = 0$ from (3), it follows $g(2.5T) = g_{\rm I}(2.5T)$, where $g_{\rm I}(t)$ is the inverse Fourier transform of ${\rm j}\cdot \ G_{\rm I}(f)$. It holds:
- $${\rm j} \cdot G_{\rm I}(f) = {\rm j} \cdot\left[ \delta(f + f_{\rm Nyq}) - \delta(f - f_{\rm Nyq})\right] \star D(f) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} g_{\rm I}(t) = 2 \cdot {\rm sin} ( 2 \pi\cdot f_{\rm Nyq} \cdot t )\cdot d(t)\hspace{0.05cm}.$$
- The sine function enforces the required zero crossings at multiples of $T = 100 \, \rm µ s$.
- $D(f)$ is a triangular function around $f = 0$ with $D(f = 0) = B$ and one-sided width $f_{0}= f_{2} - f_{\rm Nyq} = f_{\rm Nyq} - f_{1} = 2 \, \rm kHz$.
- For the associated time function we can thus write according to the specification:
- $$g_{\rm I}(t ) = 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2 \pi\cdot f_{\rm Nyq} \cdot t)\cdot {\rm sinc}^2( f_{\rm 0} \cdot t) \hspace{0.05cm}.$$
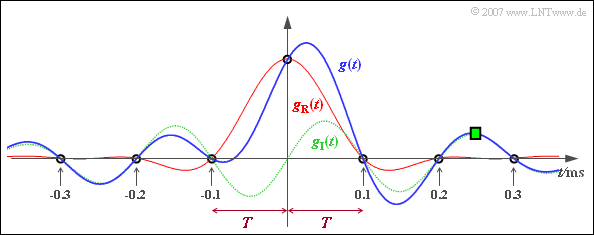
- In particular, for time $t = 250 \, \rm µ s$ (green square):
- $$g(t = 2.5 T) = g_{\rm I}(t = 2.5 T) = \ 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2.5 \pi )\cdot {\rm sinc}^2(0.5)= \ \frac{8}{\pi^2} \cdot B \cdot f_0 = \ \frac{8}{\pi^2} \cdot 10^{-4 }\,\frac{\rm V}{\rm Hz}\cdot 2 \cdot 10^{3} \,{\rm Hz}\hspace{0.1cm}\underline {= 0.162\,{\rm V}} \hspace{0.05cm}.$$
The diagram shows the change of the time function due to the imaginary part (green time course):
- The result is now an asymmetric function curve $g(t)$, shown in blue.
- However, the zero crossings of $g_{\rm R}(t)$ at the distance $T$ remain.