Exercise 2.11Z: Arithmetic Coding once again

• Return to book

Preset interval ranges

Here we consider arithmetic coding  $(\rm AC)$.  All necessary information about this type of entropy coding can be found in  Exercise 2.11.

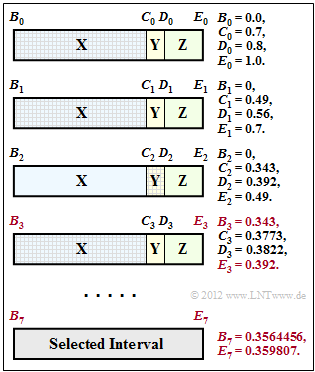
The graph is also the result of Exercise 2.11.  The numerical values for coding steps 3 and 7 that are important for the current task are highlighted in colour:

• The interval for  $N= 3$  $($symbol sequence  $\rm XXY)$  starts at  $B_3 = 0.343$  and goes up to  $E_3 = 0.392$.
• The interval limits for  $N= 7$  $($symbol sequence  $\rm XXYXXXZ)$  are  $B_7 = 0.3564456$  and  $E_7 =0.359807$.

This task is only about assigning binary sequences to the selected intervals. Procedure:

• The interval  $I$  is determined by the beginning  $B$, the end  $E$,  the interval width  ${\it \Delta} = E-B$  as well as the interval centre  $M = (B+E)/2$.
• The interval  $I$  is characterised by the binary representation  (with limited resolution)  of any real number value  $r \in I$.  For example, one chooses  $r \approx M$.
• The required number of bits results from the interval width according to the following equation  (the open square brackets mean  "round up"):

$$N_{\rm bits} = \left\lceil{\rm log_2} \hspace{0.15cm} 1/{\it \Delta} \right\rceil+1\hspace{0.05cm}. $$

For example, for  $N_{\rm bits} = 5$  the binary code  01001  stands for the following real-valued number  $r$:

$$r = 0 \cdot 2^{-1}+1 \cdot 2^{-2}+0 \cdot 2^{-3}+0 \cdot 2^{-4}+1 \cdot 2^{-5} = 0.28125 \hspace{0.05cm}. $$

Hints:

• The exercise belongs to the chapter  Further source coding methods.
• In particular, reference is made to the page  Arithmetic Coding.
• Further information on the topic can also be found in this  Wikipedia article.

Questions

1

How many bits are used to represent the source symbol sequence  $\rm XXY$   ⇒   $N = 3$ ?

$N_\text{bits} \ = \ $

2

Which arithmetic code  $\rm (AC)$  applies to this case?

	$\rm AC = $  01011,
	$\rm AC = $  010111,
	$\rm AC = $  110111.

3

How many bits are used to represent the source symbol sequence  $\rm XXYXXXZ$   ⇒   $N = 7$ ?

$N_\text{bits} \ = \ $

4

Is  01011100001  a valid code for the source symbol sequence  $\rm XXYXXXZ$?

	Yes.
	No.

5

Which statements apply to arithmetic coding in general?

	It is a common coding of entire sequences.
	A computer with 32-bit architecture limits the sequence length  $N$.
	This problem can be circumvented by integer realisation.
	Integer realisation increases the coding speed.

Solution

Solution

(1)  The selected interval begins at  $B_3 = 0.343$  and ends at  $E_3 = 0.392$.

• The interval width is therefore  ${\it \Delta}_3 = 0.049$  and thus the following applies with the logarithm to base 2:

$$N_{\rm bits} = {\rm log_2} \hspace{0.15cm} \left\lceil \frac{1}{0.049}\right\rceil+1\hspace{0.15cm}\underline{= 6} \hspace{0.05cm}.$$

(2)  The selected interval results in  $I = \big[0.343, \ 0.392\big)$.

• The middle lies at  $M_3 = 0.3675$.
• To determine the arithmetic code, we try to reach the centre of the interval as well as possible by using a binary representation.
• Since we do not have a corresponding tool for solving this task at the moment, we assume the following secondary calculations:

 $H_4 = 2^{-2} + 2^{-4} = 0.3125$   ⇒   does not belong to interval  $I$.

 $H_5 = H_4 +2^{-5} = 0.34375 \in I$   ⇒   binary representation:   0.01011  ⇒  Code:   01011.

 $H_6 = H_5 +2^{-6} = 0.359375 \in I$   ⇒   binary representation:   0.010111  ⇒  Code:   010111.

 $H_7 = H_6 +2^{-7} = 0.3671875 \in I$   ⇒   binary representation:   0.0101111  ⇒  Code:   0101111.

 $H_{12} = H_7 +2^{-12} = 0.3674316406 \in I$   ⇒   binary representation:   0.010111100001  ⇒  Code:   010111100001.

The corresponding 6–bit code is therefore  $\rm AC =$  010111   ⇒   Correct is  solution suggestion 2.

(3)  Here, with the beginning  $B_7 = 0.3564456$  and the end  $E_7 = 0.359807$  the interval width is  ${\it \Delta}_7 = 0.0033614$  and thus

$$N_{\rm bits} = \left\lceil {\rm log_2} \hspace{0.15cm} \frac{1}{0.0033614} \right\rceil + 1\hspace{0.15cm} = \left\lceil {\rm log_2} \hspace{0.15cm} 297.5 \right\rceil + 1\hspace{0.15cm} \underline{= 11} \hspace{0.05cm}.$$

(4)  The binary representation of the code  01011100001  results in

$$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-6}+ 2^{-11} = 0.3598632813 > E_7 \hspace{0.05cm}.$$

• The correct answer is therefore NO.  The valid arithmetic code is  $\rm AC =$  01011011101, because of

$$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-7}+ 2^{-8}+ 2^{-9}+ 2^{-11} =0.3579101563 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} B_7 \le 0.3579101563 < E_7.$$

(5)  All statements are correct. See also   this Wikipedia article.