Exercise 2.13: Decoding at RSC (7, 3, 5) to Base 8

ELP allocation schemes for $r = 1, \ r = 2, \ r = 3$

In the "Exercise 2.12" we used the so-called Petersen algorithm

for error correction respective

for decoding

the Reed–Solomon code $(7, \, 4, \, 4)_8$ which can due to the minimum distance $d_{\rm min} = 4$ $(t = 1)$ only correct one symbol error.

In this exercise we now consider the ${\rm RSC} \, (7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5 \ \Rightarrow \ t = 2$, whose parity-check matrix is as follows:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4}\\ 1 & \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2} & \alpha^{6} & \alpha^{3} \end{pmatrix} .$$

The received word under consideration $\underline{y} = (\alpha^2, \, \alpha^3, \, \alpha, \, \alpha^5, \, \alpha^4, \, \alpha^2, \, 1)$ results in the syndrome

$$\underline{s} = \underline{y} \cdot \mathbf{H}^{\rm T} = (0, \, 1, \, \alpha^5, \, \alpha^2).$$

The further decoding procedure is done according to the following theory pages:

Step $\rm (B)$: "Set up/evaluate the ELP coefficient vector"; "ELP" stands for "Error Locator Polynomial".

Step $\rm (C)$: "Localization of error positions",

Step $\rm (D)$: "Final error correction".

Hints:

This exercise belongs to the chapter "Error correction According to Reed–Solomon Coding".

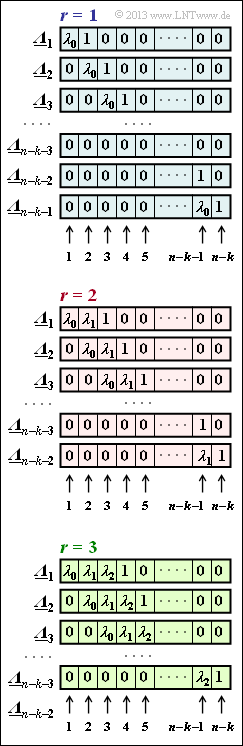
In the above graphic you can see the assignments of the "ELP coefficients" ${\it \underline{\Lambda}}_l$ assuming that there are symbol errors in the received words $r = 1, \ r = 2$ respectively. $r = 3$ .

Questions

Solution

(1) Correct are the proposed solutions 1 and 2:

The ${\rm RSC} \, (7, \, 3, \, 5)_8$ can correct up to $t = 2$ symbol errors.

The actual symbol error count $r$ must not be larger.

Conversion tables for $\rm GF(2^3)$

(2) Assuming $r = 1$, the $n-k-1$ governing equations ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ for $\lambda_0$ are as follows :

$$\lambda_0 \cdot 0 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} 1 = 0 \hspace{0.75cm} \Rightarrow \hspace{0.3cm} \lambda_0 \hspace{0.15cm} {\rm unspecified} \hspace{0.05cm},$$

$$\lambda_0 \cdot 1 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \alpha^5 = 0 \hspace{0.55cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^5 \hspace{0.05cm},$$

$$\lambda_0 \cdot \alpha^5 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \alpha^2 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{-3} = \alpha^4 \hspace{0.05cm}.$$

The assumption $r = 1$ would be justified only if the same $\lambda_0$ value resulted from all these three equations.

This is not the case here ⇒ Answer NO.

(3) Assuming the occupation for $r = 2$, we obtain two equations of determination for $\lambda_0$ and $\lambda_1$:

$$\lambda_0 \cdot 0 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \lambda_1 \cdot 1 +\alpha^5 = 0 \hspace{0.38cm} \Rightarrow \hspace{0.3cm} \lambda_1 = \alpha^5 \hspace{0.05cm},$$

$$\lambda_0 \cdot 1 \hspace{-0.15cm} \ + \ \hspace{-0.15cm} \lambda_1 \cdot \alpha^5 +\alpha^2 = 0 \hspace{0.15cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{5+5} +\alpha^2 = \alpha^{3} +\alpha^2 =\alpha^{5} \hspace{0.05cm}.$$

The system of equations can be solved under the assumption $r = 2$ ⇒ Answer YES.

The results $\lambda_0 = \lambda_1 = \alpha^5$ obtained here are processed in the next subtask.

(4) With the result $\lambda_0 = \lambda_1 = \alpha^5$, the error locator polynomial $($"key equation"$)$ is:

$${\it \Lambda}(x)=x \cdot \big ({\it \lambda}_0 + {\it \lambda}_1 \cdot x + x^2 \big ) =x \cdot \big (\alpha^5 + \alpha^5 \cdot x + x^2 )\hspace{0.05cm}.$$

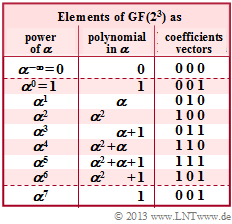
This function has zeros for $x = \alpha^2$ and $x = \alpha^3$:

$${\it \Lambda}(x = \alpha^2 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^2 \cdot \big ( \alpha^5 + \alpha^7 + \alpha^4 \big ) = \alpha^2 \cdot \big ( \alpha^5 + 1 + \alpha^4 \big )= 0\hspace{0.05cm},$$

$${\it \Lambda}(x = \alpha^3 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^3 \cdot \big ( \alpha^5 + \alpha^8 + \alpha^6 \big ) = \alpha^3 \cdot \big ( \alpha^5 + \alpha + \alpha^6 \big )= 0\hspace{0.05cm}.$$

Falsified are consequently the symbols at positions 2 and 3 ⇒ Solutions 3 and 4.

(5) After the result of the subtask (4) only the last two proposed solutions come into question:

$$\underline{e} = (0, \, 0, \, e_2, \, e_3, \, 0, \, 0, \, 0).$$

The approach is therefore accordingly $\underline{e} \cdot \mathbf{H}^{\rm T} = \underline{s}$:

$$(0, 0, e_2, e_3, 0, 0, 0) \cdot \begin{pmatrix} 1 & 1 & 1 & 1\\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1\\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^5\\ \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^2\\ \alpha^5 & \alpha^{3} & \alpha^{1} & \alpha^6\\ \alpha^6 & \alpha^{5} & \alpha^{4} & \alpha^3 \end{pmatrix} \hspace{0.15cm}\stackrel{!}{=} \hspace{0.15cm} (0, 1, \alpha^5, \alpha^2) \hspace{0.05cm}. $$

$$\Rightarrow \hspace{0.3cm} e_2 \cdot \alpha^{2} \hspace{-0.15cm} \ + \ \hspace{-0.15cm} e_3 \cdot \alpha^{3} = 0 \hspace{0.05cm}, \hspace{0.8cm} e_2 \cdot \alpha^{4} + e_6 \cdot \alpha^{3} = 1\hspace{0.05cm},\hspace{0.8cm} e_2 \cdot \alpha^{6} \hspace{-0.15cm} \ + \ \hspace{-0.15cm} e_3 \cdot \alpha^{2} = \alpha^{5} \hspace{0.05cm}, \hspace{0.6cm} e_2 \cdot \alpha^{1} + e_6 \cdot \alpha^{5} = \alpha^{2} \hspace{0.05cm}. $$

All four equations are satisfied with $e_2 = 1$ as well as $e_3 = \alpha^6$ ⇒ Proposed solution 3:

$$\underline {e} = (0, \hspace{0.05cm}0, \hspace{0.05cm}1, \hspace{0.05cm}\alpha^6, \hspace{0.05cm}0, \hspace{0.05cm}0, \hspace{0.05cm}0) $$

With $\alpha + 1 = \alpha^3$ and $\alpha^5 + \alpha^6 = \alpha$ we get from the given received word $\underline{y} = (\alpha^2, \, \alpha^3, \, \alpha, \, \alpha^5, \, \alpha^4, \, \alpha^2, \, 1)$ to the decoding result

$$\underline {z} = (\alpha^2, \hspace{0.05cm}\alpha^3, \hspace{0.05cm}\alpha^3, \hspace{0.05cm}\alpha, \hspace{0.05cm}\alpha^4, \hspace{0.05cm}\alpha^2, \hspace{0.05cm}1) \hspace{0.05cm}. $$

In the "Exercise 2.7" it was shown that this is a valid code word of ${\rm RSC} \, (7, \, 3, \, 5)_8$.

The corresponding information word is $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$.

	Symbol 0,
	Symbol 1,
	Symbol 2,
	Symbol 3,
	Symbol 4,
	Symbol 5,
	Symbol 6.

	$\underline{e} = (1, \, 0, \, 0, \, 0, \, 0, \, 0, \, \alpha^6)$,
	$\underline{e} = (\alpha^6, \, 0, \, 0, \, 0, \, 0, \, 0, \, 1)$,
	$\underline{e} = (0, \, 0, \, 1, \, \alpha^6, \, 0, \, 0, \, 0)$,
	$\underline{e} = (0, \, 0, \, \alpha^6, \, 1, \, 0, \, 0, \, 0)$.

	The schema highlighted in blue $(r = 1)$.
	The schema highlighted in red $(r = 2)$.
	The scheme highlighted in green $(r = 3)$.

	YES.
	NO.

	YES.
	NO.