Exercise 3.10Z: BSC Channel Capacity

Entropies of "BC" and "BSC"

The channel capacity $C$ was defined by Claude E. Shannon as the maximum mutual information, whereby the maximization refers solely to the source statistics:

$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$

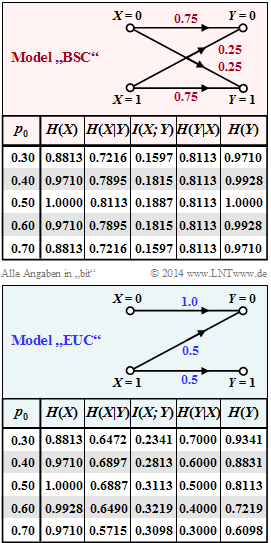
In the binary channel with the probability function $P_X(X) = \big [p_0, \ p_1 \big]$ only one parameter is optimizable, for example $p_0$ . The probability for a $1$ is thus also fixed: $p_1 = 1 - p_0.$

The upper graph (reddish background) summarises the results for the asymmetric binary channel with $ε_0 = 0.01$ and $ε_1 = 0.2$ , which was also considered in the theory section.

The maximization leads to the result $p_0 = 0.55$ ⇒ $p_1 = 0.45$ , and one obtains for the channel capacity:

$C_{\rm BC} = \hspace{-0.05cm} \max_{P_X(X)} \hspace{0.1cm} I(X;Y) \big |_{p_0 \hspace{0.05cm} = \hspace{0.05cm}0.55} \hspace{0.05cm}=\hspace{0.05cm} 0.5779\,{\rm bit} \hspace{0.05cm}.$

In the lower graph (blue background), the same information-theoretical quantities are given for the Binary Symmetric Channel $\rm (BSC)$ with the falsification probabilities $ε_0 = ε_1 = ε = 0.1$ , which was also assumed for Exercise 3.10.

In the present exercise you are

to analyze the entropies $H(X)$ , $H(Y)$ , $H(X|Y)$ and $H(Y|X)$ ,
to optimize the source parameter $p_0$ with respect to maximum mutual information $I(X; Y)$ ,
to determine the channel capacity $C(ε)$ ,
to give a closed equation for $C(ε)$ by generalization for the BSC channel model $($ initially for $ε = 0.1)$ .

Hints:

The exercise belongs to the chapter Application to digital signal transmission.
Reference is made in particular to the page Channel capacity of a binary channel.

Questions

	The equivocation results in $H(X\|Y) = H_{\rm bin}(ε)$ .
	The irrelevance results in $H(Y\|X) = H_{\rm bin}(ε)$ .
	The irrelevance results in $H(Y\|X) = H_{\rm bin}(p_0)$ .

	The channel capacity is equal to the maximum mutual information.
	For the BSC, maximization leads to the result $p_0 = p_1 = 0.5$ .
	For $p_0 = p_1 = 0.5$ , $H(X) = H(Y) = 1 \ \rm bit$ .

$ε = 0.0\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \$

$\ \rm bit$

$ε = 0.1\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \$

$\ \rm bit$

$ε = 0.5\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \$

$\ \rm bit$

$ε = 1.0\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \$

$\ \rm bit$

$ε = 0.9\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \$

$\ \rm bit$

Solution

(1) The proposed solution 2 is correct, as the following calculation shows:

$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = p_0 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} + p_0 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} +p_1 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + p_1 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon}$

$\Rightarrow \hspace{0.3cm} H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = (p_0 + p_1) \cdot \left [ \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} \right ] \hspace{0.05cm}.$

With $p_0 + p_1 = 1$ and the binary entropy function $H_{\rm bin}$ , one obtains the proposed result: $H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H_{\rm bin}(\varepsilon)\hspace{0.05cm}.$
For $ε = 0.1$ we get $H(Y|X) = 0.4690 \ \rm bit$ . The same value stands for $p_0=0.50$ in the given table.
From the table one can also see that for the BSC model (blue background) as well as for the more general (asymmetric) BC model (red background)
the equivocation $H(X|Y)$ depends on the source symbol probabilities $p_0$ and $p_1$ . It follows that proposed solution 1 cannot be correct.
The irrelevance $H(Y|X)$ is independent of the source statistics, so that solution proposal 3 can also be excluded.

(2) All given alternative solutions are correct:

The channel capacity is defined as the maximum mutual information, where the maximization has to be done with respect to $P_X = (p_0, p_1)$ :

$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$

The equation is generally valid, i.e. also for the unbalanced binary channel highlighted in red.
The mutual information can be calculated, for example, as $I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$ ,
where according to subtask (1) the term $H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$ is independent of $p_0$ or $p_1 = 1- p_0$ .
The maximum mutual information thus results exactly when the sink entropy $H(Y)$ is maximum. This is the case for $p_0 = p_1 = 0.5$ :

$H(X) = H(Y) = 1 \ \rm bit.$

Binary entropy function and BSC channel capacity

(3) According to the subtasks (1) and (2) one obtains for the BSC channel capacity:

$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$

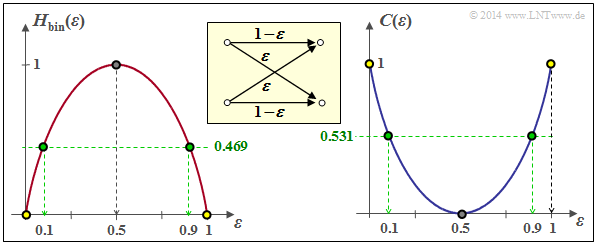
The graph shows the binary entropy function on the left and the channel capacity on the right. One obtains:

for $ε = 0.0$ (error-free channel):
$C = 1\ \rm (bit)$ ⇒ dot with yellow filling,
for $ε = 0.1$ (considered so far):
$C = 0.531\ \rm (bit)$ ⇒ dot with green filling,
for $ε = 0.5$ (completely disturbed):
$C = 0\ \rm (bit)$ ⇒ dot with grey filling.

(4) From the graph one can see that from an information-theoretical point of view $ε = 1$ is identical to $ε = 0$ :

$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}1} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0} \hspace{0.15cm} \underline {=1\,{\rm (bit)}} \hspace{0.05cm}.$

The channel only carries out a renaming here. This is called "mapping".
Every $0$ becomes a $1$ and every $1$ becomes a $0$ . Accordingly:

$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.9} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.1} \hspace{0.15cm} \underline {=0.531\,{\rm (bit)}} \hspace{0.05cm}$