Exercise 3.1: Probabilities when Rolling Dice
From LNTwww
(Redirected from Aufgabe 3.1: Wahrscheinlichkeiten beim Würfeln)
Sum $S= R + B$ of two dice
We consider the random experiment »rolling one or two dice«. Both dice are fair (the six possible outcomes are equally probable) and distinguishable by their colors:
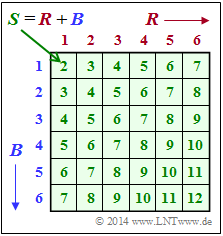
- The random quantity $R = \{1, \ 2,\ 3,\ 4,\ 5,\ 6 \}$ denotes the number of eyes of the red cube.
- The random quantity $B = \{1,\ 2,\ 3,\ 4,\ 5,\ 6 \}$ denotes the number of eyes of the blue cube.
- The random quantity $S =R + B$ stands for the sum of both dice.
In this exercise different probabilities are to be computed with reference to the random variables $R$, $B$ and $S$,
whereby the scheme indicated above can be helpful. This includes the sum $S$ as a function of $R$ and $B$.
Hints:
- The exercise belongs to the chapter Some preliminary remarks on 2D random variables.
- In particular, the subject matter of the chapter Probability Calculation in the book "Theory of Stochastic Signals" is repeated here.
Questions
Solution
(1) Assuming fair dice, the probability that
a "6" is rolled with the red die:
- $$\underline{{\rm Pr}(R=6) = 1/6} = 0.1667 \hspace{0.05cm},$$
- that a "1" or a "2" is rolled with the blue die:
- $$\underline{{\rm Pr}(B\le 2) = 1/3} = 0.3333 \hspace{0.05cm},$$
- that both dice show the same number of points:
- $$\underline{{\rm Pr}(R=B) = 6/36} = 0.1667 \hspace{0.05cm}.$$
The latter is based on the 2D representation on the specification sheet and on the "Classical Definition of Probability" corresponding to $K/M$:
- $K = 6$ of the total $M = 36$ equally probable elementary events $R \cap B$ can be assigned to the event $R=B$ derived from this.
- These lie on the diagonal. Dice players speak in this case of a "double".
(2) The solution is again based on the Classical Definition of Probability:
- In $K = 2$ of the $M = 36$ elementary fields there is a "3" ⇒ ${\rm Pr}(S = 3) = 2/36\hspace{0.15cm}\underline{ = 0.0556}.$
- In $K = 6$ of the $M = 36$ elementary fields there is a "7" ⇒ ${\rm Pr}(S = 7) = 6/36\hspace{0.15cm}\underline{ = 0.1667}.$
- In $K = 18$ of the $M = 36$ fields there is an odd number ⇒ ${\rm Pr}(S\text{ is odd}) = 18/36\hspace{0.15cm}\underline{ = 0.5}.$
- This last result could be obtained in another way:
- $${\rm Pr}(S\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}) = {\rm Pr}\big [(R\hspace{0.12cm}{\rm is \hspace{0.15cm} odd}) \cap (B\hspace{0.12cm}{\rm is\hspace{0.12cm} even}) \big ] + {\rm Pr}\big [(R\hspace{0.12cm}{\rm is\hspace{0.12cm} even}) \cap (B\hspace{0.12cm}{\rm is\hspace{0.12cm} odd})\big ]\hspace{0.05cm}. $$
- With ${\rm Pr}(R\hspace{0.12cm}{\rm is\hspace{0.12cm} even}) = {\rm Pr} (R\hspace{0.12cm}{\rm is\hspace{0.12cm} odd}) = {\rm Pr}(B\hspace{0.12cm}{\rm is\hspace{0.12cm} even})= {\rm Pr}(B\hspace{0.12cm}{\rm is\hspace{0.12cm} odd}) = 1/2$ it also follows:
- $${\rm Pr}(S\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}) = 1/2 \cdot 1/2 + 1/2 \cdot 1/2 = 1/2 \hspace{0.05cm}.$$
(3) The probability for the event that at least one of the two dice shows a "6" is:
- $${\rm Pr}\big [(R= 6) \cup (B= 6) \big ] = K/M = 11/36 \hspace{0.15cm} \underline{= 0.3056} \hspace{0.05cm}.$$
- The second probability stands alone for the "double sixes":
- $${\rm Pr}\big [(R= 6) \cap (B= 6) \big ] = K/M = 1/36 \hspace{0.15cm} \underline{= 0.0278} \hspace{0.05cm}.$$
(4) The result for $L = 1$ has already been determined in subtask (3) :
- $$p_1 = {\rm Pr}\big [(R= 6) \cup (B= 6) \big ] = {11}/{36} \hspace{0.15cm} \underline{= 0.3056} \hspace{0.05cm}.$$
- The probability $p_2$ can be expressed with $p_1$ as follows:
- $$p_2 = (1 - p_1) \cdot p_1 = \frac{25}{36} \cdot \frac{11}{36} \hspace{0.15cm} \underline{= 0.2122} \hspace{0.05cm}. $$
- In words, the probability that a "6" is rolled for the first time in the second roll is equal to the probability that no "6" was rolled in the first roll ⇒ probability $1-p_1$, but there is at least one "6" in the second roll ⇒ probability $p_1$.
- Correspondingly, for the probability "first 6 in the third throw":
- $$p_3 = (1 - p_1)^2 \cdot p_1 = \frac{25}{36} \cdot \frac{25}{36} \cdot\frac{11}{36} \hspace{0.15cm} \underline{= 0.1474} \hspace{0.05cm}.$$
(5) By extending the sample solution to subtask (4) , we obtain:
- $$\text{Pr(}L\text{ is even | first „6”)}\ = p_2 \hspace{-0.05cm}+ \hspace{-0.05cm}p_4 \hspace{-0.05cm}+ \hspace{-0.05cm} p_6 \hspace{-0.05cm}+ \hspace{-0.05cm} \text{...} = (1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1) \cdot p_1 \hspace{-0.05cm}+ \hspace{-0.05cm} (1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1)^3 \cdot p_1 \hspace{-0.05cm}+ \hspace{-0.05cm}(1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1)^5 \cdot p_1 \hspace{-0.05cm}+ \hspace{-0.05cm} \text{...} = (1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1) \cdot p_1 \cdot \left [ 1 \hspace{-0.05cm}+ \hspace{-0.05cm} (1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1)^2 \hspace{-0.05cm}+ \hspace{-0.05cm} (1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1)^4 +\text{...}\hspace{0.05cm} \right ] \hspace{0.05cm}. $$
- Accordingly, we obtain for the probability of the complementary event:
- $${\rm Pr}(L\text{ is odd | first „6”)} = p_1 + p_3 + p_5 + \text{...} = p_1 \cdot \left [ 1 + (1 - p_1)^2 + (1 - p_1)^4 + \text{...} \hspace{0.15cm} \right ] \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{{\rm Pr}(L\text{ is odd | first „6”)}) } {{\rm Pr}(L\text{ is even | first „6”)})} = \frac{1}{1 - p_1} \hspace{0.05cm}. $$
- Further, must hold::
- $${\rm Pr}(L \text{ is even | first „6”)} + {\rm Pr}(L \text{ is odd | first „6”)} = 1$$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr}(L \text{ is even | first „6”)} \cdot \left [ 1 + \frac{1}{1 - p_1} \right ] = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}(L\hspace{0.15cm}{\rm is\hspace{0.15cm} even}) = \frac{1 - p_1}{2 - p_1} = \frac{25/36}{61/36} = \frac{25}{61} \hspace{0.15cm} \underline{= 0.4098} \hspace{0.05cm}.$$
