Exercise 3.7: Comparison of Two Convolutional Encoders

• Return to book

Two convolutional encoders with parameters  $n = 2, \ k = 1, \ m = 2$

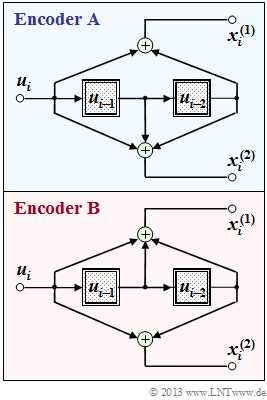
The graph shows two rate  $1/2$  convolutional encoders,  each with memory  $m = 2$:

• The encoder  $\rm A$  has the transfer function matrix $\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$.

• In encoder  $\rm B$  the two filters  $($top and bottom$)$  are interchanged,  and it holds:

$$\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2).$$

The lower encoder  $\rm B$  has already been treated in detail in the theory part.

In the present exercise, 

• you are first to determine the state transition diagram for encoder  $\rm A$, 

• and then work out the differences and the similarities between the two state diagrams.

Hints:

• This exercise belongs to the chapter  "Code description with state and trellis diagram".

• Reference is made in particular to the sections

•   "State definition for a memory register"  and.
•   "Representation in the state transition diagram".

Questions

1

  $\underline{u} = (0, \, 1, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$  holds.  Which sequences does encoder  $\rm A$ generate?

	$\underline{x}^{(1)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$,
	$\underline{x}^{(1)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$,
	$\underline{x}^{(2)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$,
	$\underline{x}^{(2)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$.

2

Which of the above state transitions exist in encoder  $\rm A$?

	$s_i = S_0, \ u_i = 0 \ ⇒ \ s_{i+1} = S_0; \hspace{1cm} s_i = S_0, \ u_i = 1 \ ⇒ \ s_{i+1} = S_1$.
	$s_i = S_1, \ u_i = 0 \ ⇒ \ s_{i+1} = S_2; \hspace{1cm} s_i = S_1, \ u_i = 1 \ ⇒ \ s_{i+1} = S_3$.
	$s_i = S_2, \ u_i = 0 \ ⇒ \ s_{i+1} = S_0; \hspace{1cm} s_i = S_2, \ u_i = 1 \ ⇒ \ s_{i+1} = S_1$.
	$s_i = S_3, \ u_i = 0 \ ⇒ \ s_{i+1} = S_2; \hspace{1cm} s_i = S_3, \ u_i = 1 \ ⇒ \ s_{i+1} = S_3$.

3

How do the two state transition diagrams differ?

	Other state transitions are possible.
	All eight transitions have different code sequences.
	Differences exist only for the code sequences  "$(01)$"  and  "$(10)$".

Solution

Solution

Calculation of the code sequence

(1)  The calculation is based on the equations

$$x_i^{(1)} = u_i + u_{i–2},$$

$$x_i^{(2)} = u_i + u_{i–1} + u_{i–2}.$$

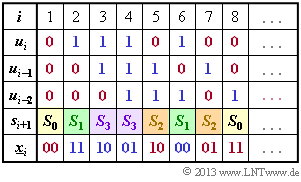
• Initially,  the two memories  $(u_{i–1}$  and  $u_{i–2})$  are preallocated with zeros   ⇒   $s_1 = S_0$.

• With  $u_1 = 0$,  we get  $\underline{x}_1 = (00)$  and  $s_2 = S_0$.

• With  $u_2 = 1$,  one obtains the output  $\underline{x}_2 = (11)$  and the new state  $s_3 = S_3$.

From the adjacent calculation scheme one recognizes the correctness of the  proposed solutions 1 and 4.

State transition diagram of encoder  $\rm A$

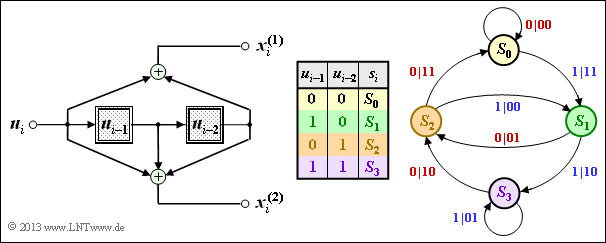
(2)  All proposed solutions  are correct:

• This can be seen by evaluating the table at subtask  (1).

• The results are shown in the adjacent graph.

State transition diagram of encoder  $\rm B$

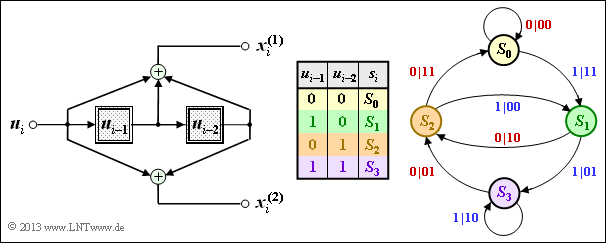
(3)  Correct is only  statement 3:

• The state transition diagram of encoder  $\rm B$  is sketched on the right.  For derivation and interpretation,  see section "Representation in the state transition diagram".

• If we swap the two output bits  $x_i^{(1)}$  and  $x_i^{(2)}$,  we get from the convolutional encoder  $\rm A$  to the convolutional encoder  $\rm B$  $($and vice versa$)$.