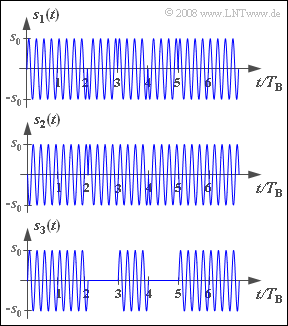
Exercise 4.7Z: Signal Shapes for ASK, BPSK and DPSK

Specified transmitted signals

The figure shows, starting from the same source signal $q(t)$, the transmitted signals with

Amplitude Shift Keying $\rm (ASK)$,
Binary Phase Shift Keying $\rm (BPSK)$,
Differential Phase Shift Keying $\rm (DPSK)$.

The transmitted signals are generally designated here as $s_1(t)$, $s_2(t)$ and $s_3(t)$. The assignment to the given modulation methods is to be done by you.

In addition, the respective average energy per bit ⇒ $E_{\rm B}$ in "Ws" is to be specified for all signals, whereby the following assumptions can be made:

The (maximum) envelope of all carrier frequency modulated signals is $s_0 = 2\ \rm V$.
The bit rate of the redundancy-free source signal is $R_{\rm B} = 1 \ \rm Mbit/s$.
The modulators operate with a working resistance of $R = 50 \ \rm Ω$.

For example, for (bipolar) baseband transmission with symbol duration $T_{\rm } = 1/R_{\rm }$ would be:

$$ E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{R} = \frac {(2\,{\rm V})^2 \cdot 10^{-6} \,{\rm s}}{50 \,{\rm V/A}}= 8 \cdot 10^{-8} \,{\rm Ws}= 0.08 \,\,{\rm µ Ws}.$$

Notes:

The exercise belongs to the chapter Linear Digital Modulation.
However, reference is also made to the chapter Basics of Coded Transmission in the book "Digital Signal Transmission".
The powers are given in $\rm V^2$; they thus refer to the reference resistor $R = 1 \ \rm \Omega$.

Questions

Solution

(1) Solution 3 is correct:

The ASK signal results from the multiplication of the here sinusoidal carrier signal $z(t)$ with the unipolar source signal $q(t)$.
It is obvious that $s_3(t)$ describes such an ASK signal.
The unipolar amplitude coefficients of the source signal are $1,\ 1,\ 0,\ 1,\ 0,\ 1,\ 1$.

(2) Compared to the bipolar baseband transmission, the following changes can be seen in ASK:

The energy is halved because of multiplication by the sinusoidal signal.
Since $q(t)$ is assumed to be redundancy-free, in half the time $s_3(t) = 0$, which halves the energy again.

This gives:

$$E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{4 \cdot R} = \frac {(2\,{\rm V})^2 \cdot 10^{-6} \,{\rm s}}{4 \cdot 50 \,{\rm V/A}}= 2 \cdot 10^{-8} \,{\rm Ws}\hspace{0.15cm}\underline {= 0.02 \,\,{\rm µ Ws}}.$$

(3) Solution 1 is correct:

Phase jumps are typical for BPSK.
Since the same source signal was always assumed, these phase jumps occur exactly when there is a symbol change in the ASK signal $s_3(t)$.

(4) Of the changes mentioned under (2) compared to baseband transmission, only the first one is applicable for BPSK. Thus:

$$E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{2 \cdot R} \hspace{0.15cm}\underline {= 0.04 \,\,{\rm µ Ws}}.$$

(5) As can already be assumed, the correct answer is $s_2(t)$ ⇒ solution 2:

The DPSK modulator operates as follows, assuming $m_0 = -1$:

$$ m_0 = -1, \hspace{0.1cm}a_1 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_1 = -1,$$

$$m_1 = -1, \hspace{0.1cm}a_2 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_2 = -1,$$

$$m_2 = -1, \hspace{0.1cm}a_3 = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_3 = +1,$$

$$m_3 = +1, \hspace{0.1cm}a_4 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_4 = +1,$$

$$m_4 = +1, \hspace{0.1cm}a_5 = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_5 = -1,$$

$$m_5 = -1, \hspace{0.1cm}a_6 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_6 = -1, \,\,{\rm etc.}$$

(6) A comparison of the two signals $s_1(t)$ and $s_2(t)$ shows that nothing changes with respect to the signal energy.

It follows: DPSK has exactly the same signal energy as BPSK:

$$E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{2 \cdot R} \hspace{0.15cm}\underline {= 0.04 \,\,{\rm µ Ws}}.$$

	$s_1(t),$
	$s_2(t),$
	$s_3(t).$

	$s_1(t),$
	$s_2(t),$
	$s_3(t)$.