Exercise 1.3: Rayleigh Fading
Rayleigh fading should be used when
- there is no direct connection between transmitter and receiver, and
- the signal reaches the receiver through many paths, but their transit times are approximately the same.
An example of such a Rayleigh channel occurs in urban mobile communications when narrow-band signals are used with ranges between $50$ and $100$ meters.
Looking at the radio signals $s(t)$ and $r(t)$ in the equivalent low-pass range $($that is, around the frequency $f = 0)$, the signal transmission is described completely by the equation
- $$r(t)= z(t) \cdot s(t)$$
The multiplicative fading coefficient
- $$z(t)= x(t) + {\rm j} \cdot y(t)$$
is always complex and has the following characteristics:
- The real part $x(t)$ and the imaginary part $y(t)$ are Gaussian mean-free random variables, both with equal variance $\sigma^2$. Within the components $x(t)$ and $y(t)$ there may be statistical dependence, but this is not relevant for the solution of the present task. We assume that $x(t)$ and $y(t)$ are uncorrelated.
- The magnitude $a(t) = |z(t)|$ has a Rayleigh PDF, from which the name "Rayleigh Fading" is derived:
- $$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^ { -a^2/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for}\hspace{0.15cm} a \ge 0 \\ {\rm for}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm}.$$
- The squared magnitude $p(t) = a(t)^2 = |z(t)|^2$ is exponentially distributed according to the equation
- $$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^ { -p/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for}\hspace{0.15cm} p \ge 0 \\ {\rm for}\hspace{0.15cm} p < 0 \\ \end{array} \hspace{0.05cm}.$$
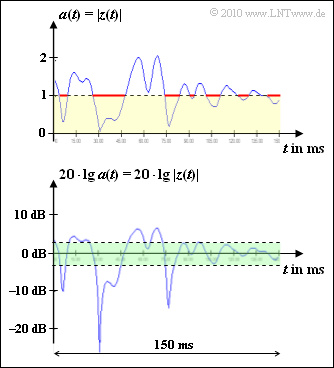
Measurements have shown that the time intervals with $a(t) ≤ 1$ $($highlighted in yellow in the graphic$)$ add up to $\text{59 ms}$ $($intervals highlighted in red$).$ Being the total measurement time $\text{150 ms}$, the probability that the magnitude of the Rayleigh fading is less than or equal to $1$ is
- $${\rm Pr}(a(t) \le 1) = \frac{59\,\,{\,{\rm ms}}}{150\,\,{\rm ms}} = 39.4 \% \hspace{0.05cm}.$$
In the lower graph, the value range between $\text{-3 dB}$ and $\text{+3 dB}$ of the logarithmic Rayleigh coefficient $20 \cdot {\rm lg} \ a(t)$ is highlighted in green. The subtask (4) refers to this.
Notes:
- This task belongs to chapter Probability density of Rayleigh fading of this book.
- A similar topic is treated with a different approach in chapter Further distributions of the book "Stochastic Signal Theory".
- To check your results, you can use the interactive applet PDF, CDF and Moments of Special Distributions of the book "Stochastic Signal Theory".
Questions
Solution
- $${\rm Max} \left [ 20 \cdot {\rm lg}\hspace{0.15cm}a(t) \right ] = 20 \cdot {\rm lg}\hspace{0.15cm}(2) \hspace{0.15cm} \underline{\approx 6\,\,{\rm dB}} \hspace{0.05cm}.$$
(2) The maximum value of the square $p(t) = a(t)^2$ is
- $${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{=4} \hspace{0.05cm}.$$
- The logarithmic representation of the squared magnitude $p(t)$ is identical to the logarithmic representation of the magnitude $a(t)$.
- Since $p(t)$ is a power quantity:
- $${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{= 4} \hspace{0.05cm}.$$
- The maximum value is thus also $\underline{\approx 6\,\,{\rm dB}}$.
(3) The condition $a(t) ≤ 1$ is equivalent to the requirement $p(t) = a(t)^2 ≤ 1$.
- The absolute square is known to be exponentially distributed, and for $p ≥ 0$ we have
- $$f_p(p) = \frac{1}{2\sigma^2} \cdot {\rm e}^{ -p/(2\sigma^2)} \hspace{0.05cm}.$$
- It follows:
- $${\rm Pr}(p(t) \le 1) = \frac{1}{2\sigma^2} \cdot \int_{0}^{1}{\rm e}^{ -p/(2\sigma^2)} \hspace{0.15cm}{\rm d}p = 1 - {\rm e}^{ -1/(2\sigma^2)} = 0.394$$
- $$\Rightarrow \hspace{0.3cm} {\rm e}^{ -1/(2\sigma^2)} =0.606 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma^2 = \frac{1}{2 \cdot {\rm ln}\hspace{0.1cm}(0.606)} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{\sigma = 1} \hspace{0.05cm}.$$
The graph shows
- on the left side the probability ${\rm Pr}(p(t) ≤ 1)$,
- on the right side the probability ${\rm Pr}(0.5 \le p(t) ≤ 2)$.
(4) From $10 \cdot {\rm lg} \ p_1 = \ -3 \ \ \rm dB$ follows $p_1 = 0.5$. The upper limit of the integration range results from the condition $10 \cdot {\rm lg} \ p_2 = +3 \ \ \rm dB$, so $p_2 = 2$.
- This gives, according to the above graph:
$${\rm Pr}(-3\,\,{\rm dB}\le 10 \cdot {\rm lg}\hspace{0.15cm}p(t) \le +3\,\,{\rm dB}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{0.5}^{2}f_p(p)\hspace{0.15cm}{\rm d}p = \left [ - {\rm e}^{ -{p}/(2\sigma^2)}\hspace{0.15cm} \right ]_{0.5}^{2} ={\rm e}^{-0.25}- {\rm e}^{-1} \approx 0.779 - 0.368 \hspace{0.15cm} \underline{ = 0.411} \hspace{0.05cm}.$$