Contents
A very general description of the mobile communication channel
To simplify the notation, the addition "TP" (Tiefpass ⇒ low-pass) is omitted in the following. Thus the real signal $s(t) = 1$ is present at the input of the mobile radio channel and the output signal $r(t)$ is complex-valued. Additional noise processes are excluded.
The radio signal $s(t)$ can reach the receiver via a large number of paths, whereby the individual signal components are attenuated in different ways and delayed for different lengths. In general, it is possible to express the received signal (in the equivalent low-pass range) without taking thermal noise into account as it follows:
- \[r(t)= \sum_{k=1}^{K} \alpha_{k}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{k}(t)} \cdot s(t - \tau_{k}) \hspace{0.05cm}.\]
The following designations are used here:
- The time dependent attenuation factor on the $k$–th path is $\alpha_k(t)$.
- The time dependent phase progression on the $k$–th path is $\phi_k(t)$.
- The time dependent runtime on the $k$–th path is $\tau_k(t)$.
The number $K$ of (at least slightly) different paths is usually very large and unsuitable for direct modeling.
- The model can be simplified considerably by combining paths with approximately equal delays.
- So you only distinguish between $M$ main paths, which are characterized by large differences in distance and thus noticeable differences in delay:
- \[r(t)= \sum_{m=1}^{M} \hspace{0.1cm} \sum_{n=1}^{N_m} \alpha_{m,\hspace{0.04cm}n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{m,\hspace{0.04cm}n}(t)} \cdot s(t - \tau_{m,\hspace{0.04cm}n}) \hspace{0.05cm}.\]
The two equations given so far are identical. A simplification results only if one replaces for each main path $m \in \{1, \hspace{0.04cm}\text{...}\hspace{0.04cm}, M\}$ the $N_m$ delays, which differ slightly due to reflections at fine structures as well as possibly due to diffraction and refraction phenomena, by a mean delay:
- \[\tau_{m} = \frac{1}{N_m} \cdot \sum_{n=1}^{N_m} \tau_{m,\hspace{0.04cm}n} \hspace{0.05cm}.\]
$\text{Conclusion:}$ This gives the following intermediate result for mobile radio: The »received signal in the equivalent low-pass range« can be represented as
- \[r(t)= \sum_{m=1}^{M} z_m(t) \cdot s(t - \tau_{m}) \hspace{0.5cm} {\rm with} \hspace{0.5cm} z_m(t) = \sum_{n=1}^{N_m} \alpha_{m,\hspace{0.04cm}n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi_{m,\hspace{0.04cm}n}(t)} \hspace{0.05cm}.\]
Frequency-selective fading vs. non-frequency-selective fading
Based on the equation just derived
- \[r(t)= \sum_{m=1}^{M} z_m(t) \cdot s(t - \tau_{m}) \hspace{0.5cm} {\rm with} \hspace{0.5cm} z_m(t) = \sum_{n=1}^{N_m} \alpha_{m,\hspace{0.04cm}n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi_{m,\hspace{0.04cm}n}(t)} \hspace{0.05cm}\]
two important special cases can be derived:
- If there is more than one main path $(M \ge 2)$, one speaks of multipath propagation. As will be shown in the second main chapter ⇒ "Frequency-selective transmission channels" then – depending on the frequency – constructive or destructive overlaps up to complete extinction occur.
- For some frequencies, multipath propagation proves to be favourable, for others, very unfavourable. This effect is called »frequency selective fading«.
With only one main path $(M = 1)$ the above equation is simplified as follows $($in this case the index "$m = 1$" will be omitted$)$:
- \[r(t)= z(t) \cdot s(t - \tau) \hspace{0.05cm}.\]
The delay $\tau$ causes here a constant transmission time for all frequencies, which does not need to be considered further.
$\text{Conclusion:}$ For $M=1$ there is no superposition of signal components with noticeable differences in propagation time, thus also no frequency dependence of the total signal:
- \[r(t)= z(t) \cdot s(t) \hspace{0.5cm} {\rm with} \hspace{0.5cm} z(t) = \sum_{n=1}^{N} \alpha_{n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{n}(t)} \hspace{0.05cm}. \]
One speaks in this case of »non-frequency selective fading« or »Flat Fading« or »Rayleigh Fading«.
Modeling of non-frequency-selective fading
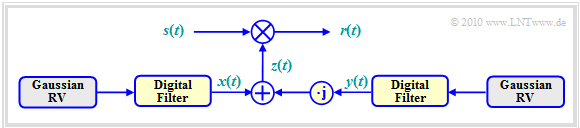
The figure shows the model for generating non-frequency selective fading ⇒ Rayleigh fading.
- The received signal $r(t)$ is obtained by multiplying the transmitted signal $s(t)$ by the time function $z(t)$.
- It should be remembered again that all signals or time functions $s(t)$, $z(t)$ and $r(t)$ refer to the equivalent low-pass range.
We now look at the multiplicative error $z(t)\ne 1$ according to this Rayleigh model more precisely. For the complex coefficient applies according to the last section:
- \[z(t) = \sum_{n=1}^{N} \alpha_{n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.04cm}\cdot \hspace{0.04cm} \phi_{n}(t) }= \sum_{n=1}^{N} \alpha_{n}(t) \cdot \cos\hspace{-0.1cm}\big [ \phi_{n}( t) \big ] + {\rm j}\cdot \sum_{n=1}^{N} \alpha_{n}(t) \cdot \sin\hspace{-0.1cm}\big [ \phi_{n}( t)\big ] \hspace{0.05cm}. \]
It should be noted about this equation and the above graph:
- The time dependent attenuation $\alpha_{n}(t)$ and the time dependent phase $\phi_{n}(t)$ depend on the environmental conditions.
- $\phi_{n}(t)$ captures the slightly different delays on the $N$ paths and the $\text{Doppler effect}$ due to the movement.
- The time function $z(t)$ is a complex quantity whose real and imaginary part denoted in the following as $x(t)$ and $y(t)$ .
- A deterministic description of the random variable $z(t) = x(t) + {\rm j}\cdot y(t)$ is not possible; the functions $x(t)$ and $y(t)$ must be modeled by stochastic processes.
- If the number $N$ of the (slightly) different delays is sufficiently large, then according to the $\text{Central Limit Theorem}$ for this $\text{Gaussian Random Variable}$.
- The two components $x(t)$ and $y(t)$ are each mean-free and have the same variance $\sigma^2$:
- \[{\rm E}[x(t)] = {\rm E}\big[y(t)\big] = 0\hspace{0.05cm}, \hspace{0.8cm}{\rm E}\big[x^2(t)\big] = {\rm E}\big[y^2(t)\big] = \sigma^2 \hspace{0.05cm}.\]
- We observe the orthogonality of the real part and the imaginary part (both cosine and sine of the same argument). Thus the two components are also uncorrelated. Only in the case of Gaussian random variables does the statistical independence of $x(t)$ and $y(t)$ follow from this.
- Because of the Doppler effect, however, there are statistical dependencies within the real part $x(t)$ and within the imaginary part $y(t)$. These two quantities are created in the above model by two $\text{Digital Filters}$.
Exemplary signal curves with Rayleigh fading
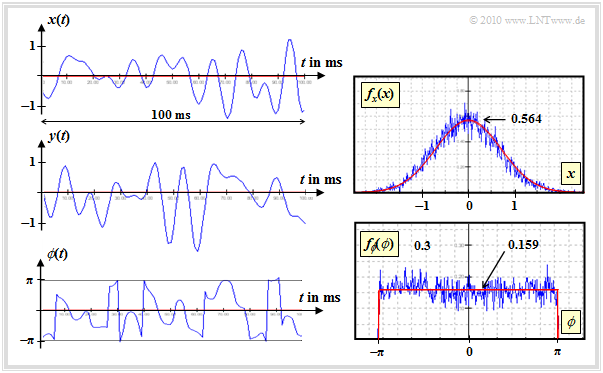
The following graphs show signal curves of $\text{100 ms}$ duration and the corresponding density functions. These are screen shots of the Windows program "Mobile Radio Channel" from the (former) practical course "Simulation of Digital Transmission Systems" at the TU Munich.
$\text{Example 1:}$ In the following, exemplary signal curves for Rayleigh fading and the corresponding probability density functions are shown. These time curve representations can be interpreted as follows:
- The real part is Gaussian distributed (see upper right graph), as shown in the signal $x(t)$. Red is the Gaussian PDF $f_x(x)$ and blue is the histogram obtained by simulation over $10\hspace{0.05cm}000$ samples.
- The parameter used was a $\text{maximum Doppler frequency}$ of $f_{\rm D, \ max} = 100 \ \rm Hz$. Therefore there are statistical bindings within the functions $x(t)$ and $y(t)$. More details about the Doppler effect can be found in the next chapter.
- The PDF $f_y(y)$ of the imaginary part is identical to $f_x(x)$. The variance is $\sigma_x^2 =\sigma_y^2 = 0. 5 \ (=\sigma^2)$. Between $x(t)$ and $y(t)$ there are no statistical bindings; the signals are orthogonal.
- The phase $\phi(t)$ is equally distributed between $\pm\pi$. As can be guessed from the jumping points in the phase function, $\phi(t)$ can also assume larger values. During the creation of the histogram, however, the ranges $(2k+1)\cdot \pi$ were projected to the value range of $-\pi$ ... $+\pi$ $(k$ integer$)$.
- The equally distributed phase can be understood by means of the (not shown) 2D–PDF. This is rotationally symmetrical and accordingly there is no preferred direction:
- \[f_{x,\hspace{0.02cm}y}(x, y) = \frac{1}{2\pi \cdot \sigma^2} \cdot {\rm e}^{ -(x^2 + y^2)/(2\sigma^2)} .\]
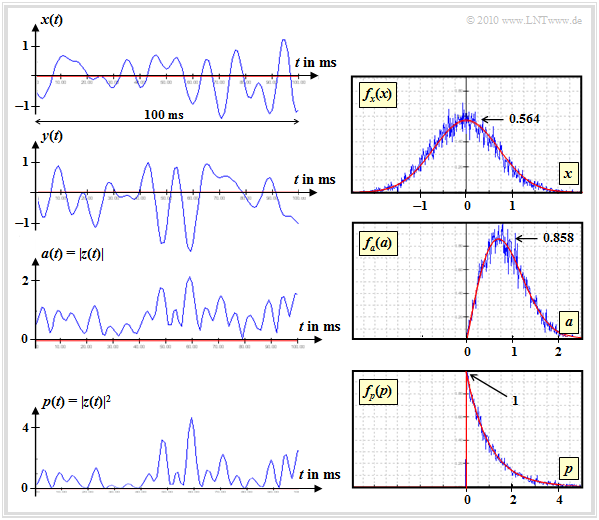
$\text{Example 2}$ in continuation to $\text{Example 1}$:
This graphic shows on the
- left: the real part $x(t)$ and the imaginary part $y(t)$ of $z(t)$ ;
- right: the PDF $f_x(x)$; the PDF $f_y(y)$ has exactly the same form.
Underneath it are the gradient and PDF
- of the magnitude $a(t) =\vert z(t)\vert$ and
- of the square $p(t) =a^2(t) =\vert z(t)\vert^2$.
From these descriptions it is clear:
- The magnitude $a(t) =\vert z(t)\vert$ has a $\text{Rayleigh PDF}$ ⇒ hence the name "Rayleigh fading":
- \[f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^{-a^2/(2\sigma^2)} \\ 0 \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm for}\hspace{0.1cm} a\hspace{-0.05cm} \ge \hspace{-0.05cm}0, \\ {\rm for}\hspace{0.1cm} a \hspace{-0.05cm}<\hspace{-0.05cm} 0. \\ \end{array} \]
- For the moments of first and second order and the variance of the absolute value function $a(t)$ applies:
- \[{\rm E}\big [a \big] = \sigma \cdot \sqrt {{\pi}/{2}}\hspace{0.05cm},\hspace{0.5cm}{\rm E}\big[a^2 \big] = 2 \cdot \sigma^2\]
- \[ \Rightarrow \hspace{0.3cm} {\rm Var}\big[a \big] = \sigma_a^2 = \sigma^2 \cdot \left ( 2 - {\pi}/{2}\right ) \hspace{0.05cm}. \]
- The PDF of the absolute value square $p(t)$ is given by $\text{nonlinear transformation}$ the PDF $f_a(a)$ ⇒ $f_p(p)$ is exponentially distributed:
- \[f_p(p) \hspace{-0.05cm}=\hspace{-0.05cm} \left\{ \begin{array}{c} (2\sigma^2)^{-1} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm e}^{-p^2\hspace{-0.05cm}/(2\sigma^2)} \\ 0 \end{array} \right.\hspace{0.05cm} \begin{array}{*{1}c} {\rm for}\hspace{0.15cm} p \hspace{-0.05cm}\ge \hspace{-0.05cm}0, \\ {\rm for}\hspace{0.15cm} p\hspace{-0.05cm} < \hspace{-0.05cm}0. \\ \end{array} \]
Further information about the Rayleigh fading can be found in the
"Exercise 1.3" and the "Exercise 1.3Z".
Exercises for the chapter
Exercise 1.3Z: Rayleigh Fading Revisited