Exercise 1.5: Rectangular-in-Frequency Low-Pass Filter

Table with values of the $\rm si$–function and the $\rm Si$–function

We consider an ideal, rectangular low-pass filter – also called a Küpfmüller low-pass filter,

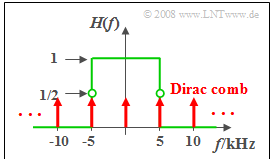
which passes all frequencies $f < 5 \ \rm kHz$ in an undistorted way ⇒ $H(f) = 1$,
and completely suppresses all spectral components above $5 \ \rm kHz$ ⇒ $H(f) = 0$.

Exactly at the cut-off frequency $f_{\rm G} = 5 \ \rm kHz$ the value of the transfer function is equal to $1/2$.

Various signals are applied to the input of the low-pass filter:

a narrow rectangular pulse of suitable height which can be approximated by a "Dirac":

$$x_1(t) = 10^{-3}\hspace{0.1cm}{\rm Vs} \cdot {\rm \delta}(t),$$

a Dirac pulse, i.e., a sum of Dirac functions evaluated at the respective time interval of $T_{\rm A}$:

$$x_2(t) = 10^{-3}\hspace{0.1cm}{\rm Vs} \cdot \sum_{\nu = -\infty}^{+\infty}{\rm \delta}(t - \nu \cdot T_{\rm A}),$$

where the associated spectrum with $f_{\rm A} = 1/T_{\rm A}$ is:

$$X_2(f) = \frac{10^{-3}\hspace{0.1cm}{\rm Vs}}{T_{\rm A}} \cdot\sum_{\mu = -\infty}^{+\infty}{\rm \delta}(f - \mu \cdot f_{\rm A}),$$

a step function at time $t = 0$:

$$x_3(t) = 10\hspace{0.1cm}{\rm V} \cdot \gamma(t) = \left\{ \begin{array}{c} 0 \\ 5\hspace{0.1cm}{\rm V} \\ 10\hspace{0.1cm}{\rm V} \\ \end{array} \right.\quad \quad\begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}{ t < 0,} \\{ t = 0,} \\ { t > 0,} \\ \end{array}$$

an $\rm si$–shaped pulse with equivalent duration $T$:

$$x_4(t) = 10\hspace{0.1cm}{\rm V} \cdot {\rm si}(\pi \cdot {t}/{T}) \hspace{0.5cm} {\rm mit} \hspace{0.5cm} {\rm si}(x) = {\rm sin}(x)/x .$$

Please note:

The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
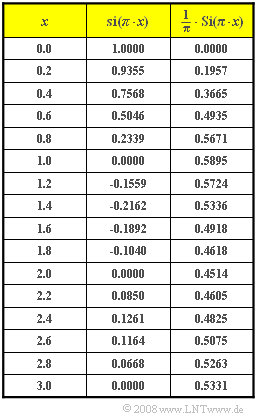
The table lists the function values of the sinc function ${\rm si}(πx)$ and the sine integral function ${\rm Si}(πx)$:

$${\rm Si}(\pi x) = \int_{ 0 }^{ x } {{\rm si} ( \pi \xi )} \hspace{0.1cm}{\rm d}\xi \hspace{0.5cm}{\rm mit } \hspace{0.5cm} {\rm si}(x) =\sin(x)/x.$$

Questions

$y_1(t = 0) \ = \ $

$\rm V$

$y_1(t = 50 {\: \rm µ s}) \ = \ $

$\rm V$

$y_2(t = 0) \ = \ $

$\rm V$

$T_{\rm A} = 199 \ {\rm µ s} \text{:}\hspace{0.4cm} y_2(t = 0) \ = \ $

$\rm V$

$T_{\rm A} = 201 \ {\rm µ s} \text{:}\hspace{0.4cm} y_2(t = 0) \ = \ $

$\rm V$

$y_3(t = 0) \ = \ $

$\rm V$

$t_{\rm max} \ = \ $

$\rm µ s$

$y_3(t_{\rm max}) \ = \ $

$\rm V$

$y_4(t = 0) \ = \ $

$\rm V$

$y_4(t = 0) \ = \ $

$\rm V$

Solution

(1) With $Δf = 10 \ \rm kHz$, the impulse response of the ideal low-pass filter is given by:

$$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t ).$$

The output signal differs from this by the weighting factor $\rm 10^{–3} \ \rm Vs$:

$$y_1(t) = 10^{-3}\hspace{0.1cm}{\rm Vs} \cdot 10^{4}\hspace{0.1cm}{\rm Hz} \cdot {\rm si}(\pi \cdot \Delta f \cdot t ) = 10\hspace{0.1cm}{\rm V} \cdot {\rm si}(\pi \cdot \Delta f \cdot t )$$

$$ \Rightarrow \hspace{0.2cm}y_1(t = 0) \hspace{0.15cm}\underline{=10\hspace{0.1cm}{\rm V}},\hspace{0.5cm}y_1(t = 50\hspace{0.1cm}{\rm µ s}) =10\hspace{0.1cm}{\rm V} \cdot {\rm si} \left( {\pi}/{2} \right) \hspace{0.15cm}\underline{= 6.37\hspace{0.1cm}{\rm V}}.$$

Dirac pulse and rectangular filter

(2) The spectrum $X_2(f)$ contains discrete lines at an interval of $f_{\rm A} = 1/T_{\rm A} = 5 \ \rm kHz$, each with weight $5 \ \rm V$.

The spectrum $Y_2(f)$ thus consists of one spectral line at $f = 0$ with weight $5 \ \rm V$ and one each at $±5 \ \rm kHz$ with weight $2.5 \ \rm V$. Hence, the following is true for the time signal:

$$ y_2(t) = 5 \hspace{0.1cm}{\rm V} + 5\hspace{0.1cm}{\rm V} \cdot{\rm cos}(2 \pi \cdot f_{\rm A} \cdot t ) = 10\hspace{0.1cm}{\rm V} \cdot {\rm cos}^2(\pi \cdot f_{\rm A} \cdot t ).$$

$$ \Rightarrow \hspace{0.3cm} y_2(t= 0) \hspace{0.15cm} \underline{ = 10\hspace{0.1cm}{\rm V}} .$$

(3) Due to $T_{\rm A} = 199 \ \rm µ s $ , $f_{\rm A} > 5 \ \rm kHz$ holds. Because of $H(f_{\rm A}) = 0$ the spectrum consists of only one spectral line at $f = 0$ with weight $5.025 \ \rm V$ and the following constant curve is obtained

$$ \Rightarrow \hspace{0.3cm} y_2(t) \rm \underline{\: = 5.025 \ \rm V}.$$

If $T_{\rm A}$ is further decreased, the output still yields a direct signal but with larger signal value (proportional to $1/T_{\rm A}$).

In contrast to this, with $T_{\rm A} = 201 \ \rm µ s $ the sampling frequency is slightly smaller than the cut-off frequency of the filter $(5 \ \rm kHz)$ and the spectral function of the output signal is:

$$Y_2(f) = 4.975\hspace{0.1cm}{\rm V} \cdot \big[ {\rm \delta}(f ) + {\rm \delta}(f + f_{\rm A}) + {\rm \delta}(f - f_{\rm A})\big].$$

From this it follows for the time signal:

$$y_2(t ) = 4.975\hspace{0.1cm}{\rm V} + 9.95\hspace{0.1cm}{\rm V} \cdot {\rm cos}(2 \pi \cdot f_{\rm A} \cdot t ) \hspace{0.2cm} \Rightarrow \hspace{0.2cm}y_2(t = 0) \hspace{0.15cm}\underline{=14.925\hspace{0.1cm}{\rm V}}.$$

Nothing changes in the fundamental curve as long as $ 200 \ {\rm µ s} < T_{\rm A} < 400 \ {\rm µ s} $ holds.
However, different amplitudes arise as a result depending on $T_{\rm A}$ . For $T_{\rm A} ≥ 400 \ {\rm µ s}$ additional spectral lines are added.

Impulse response and step response

(4) The output signal $y_3(t)$ now goes according to the sine integral function:

$$y_3(t = 0) = 10\hspace{0.1cm}{\rm V} \cdot \Delta f \cdot \int_{ - \infty }^{ t } \hspace{-0.3cm} {{\rm si} ( \pi \Delta f \tau )} \hspace{0.1cm}{\rm d}\tau = 10\hspace{0.1cm}{\rm V} \cdot \big[ {1}/{2} + {1}/{\pi}\cdot {\rm Si} ( \pi \Delta f t )\big].$$

$$ \Rightarrow \hspace{0.3cm} y_3(t= 0) \hspace{0.15cm} \underline{ = 5\hspace{0.1cm}{\rm V}} .$$

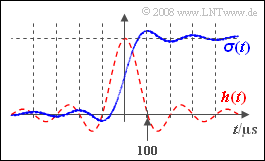
(5) It is obvious that $y_3(t)$ attains its maximum when the ${\rm si}$–function intersects the abscissa for the first time at positive times (see sketch). So, it must hold::

$$t_{\rm max} = 1/Δf \rm \underline{\: = 100 \: µ s}.$$

The signal value is obtained according to the table on the information page and is

$$y_3(t = t_{\rm max}) = 10\hspace{0.1cm}{\rm V} \cdot \big[ {1}/{2} + {1}/{\pi}\cdot {\rm Si} ( \pi )\big]= 10\hspace{0.1cm}{\rm V} \cdot \big[ 0.5 + 0.5895 \big] \hspace{0.15cm}\underline{= 10.895 \hspace{0.1cm}{\rm V}} .$$

At later times $t$ , $y_3(t)$ slowly adjusts to its final value $10 \ \rm V$.

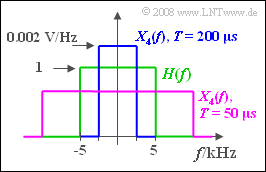
Rectangular spectra at the input of the rectangular filter

(6) The spectral function $X_4(f)$ is rectangular like $H(f)$ and for $|f| > 2.5 \ \rm kHz$ always zero.

This means that $Y_4(f ) = X_4(f)$ holds and so does $y_4(t) = x_4(t)$.
Thus, $y_4(t = 0) \rm \underline{\: = 10 \: \rm V}$.

(7) Due to $T = 50 \ \rm µ s$ , $X_4(f)$ has the width $20 \ \rm kHz$ and the height $0.5 · 10 ^{-3} \ \rm V/Hz$.

The spectral function $Y_4(f)$ has the same height after being multiplied by $H(f)$ .
The width $10 \ \rm kHz$ is now determined exclusively by $H(f)$ :

$$y_4(t) = 0.5 \cdot 10^{-3}\hspace{0.1cm}{ {\rm V} }/{ {\rm Hz} } \cdot 10 \hspace{0.1cm}{\rm kHz} \cdot {\rm si}(\pi \Delta f t ) = 5\hspace{0.1cm}{\rm V} \cdot {\rm si}(\pi \Delta f t )$$

$$ \Rightarrow \hspace{0.3cm}y_4(t = 0) \hspace{0.15cm}\underline{=5\hspace{0.1cm}{\rm V} }.$$