Exercise 1.6: Rectangular-in-Time Low-Pass Filter
From LNTwww
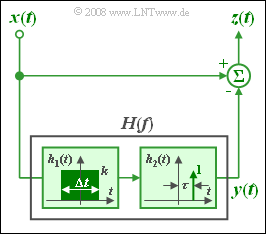
We consider below the constellation shown in the graph:
- The frequency response $H(f) = H_1(f) · H_2(f)$ in the lower branch is determined by the impulse responses of its two subcomponents.
- Here, $h_1(t)$ is constantly equal to $k$ in the reange from $-1\ \rm ms$ to $+1\ \rm ms$ and zero outside.
- At the range limits, half the value is valid in each case.
- The time variable drawn in the figure is thus $Δt = 2 \ \rm ms$.
The impulse response of the second system function $H_2(f)$ is:
- $$h_2(t) = \delta(t - \tau).$$
The frequency response between the signals $x(t)$ and $z(t)$ is of high-pass character and generally:
- $$H_{\rm HP}(f) = 1 - H_1(f) \cdot {\rm e}^{-{\rm j\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi}f \tau}.$$
- For the subtasks (1) to (4) the following holds: $τ = 0$ ⇒ $H(f) = H_1(f)$.
- However, using $τ = 0$ this can also be formulated as follows $(Δt = 2 \ \rm ms)$:
- $$H_{\rm HP}(f) = 1 - {\rm si}( \pi \cdot {\rm \Delta}t \cdot f).$$
- With no effect on the solution of the problem, note that this equation is not applicable for $τ ≠ 0$ because of:
- $$|H_{\rm HP}(f)|\hspace{0.09cm} \ne \hspace{0.09cm}1 - |H_1(f)| .$$
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- In particular, reference is made to the page Slit low-pass filter.
Questions
Solution
(1) The condition $H(f = 0) = 1$ means that the area of the impulse response is equal to $1$ . From this it follows that:
- $$k = {1}/{\Delta t} \hspace{0.15cm}\underline{= 500\hspace{0.1cm}{ 1/{\rm s}}} .$$
(2) Approaches 2 and 4 are correct:
- The output signal $y(t)$ is obtained as the convolution product of $x(t)$ and $h(t)$.
- Convolution of two rectangles of equal width results in a triangle with its maximum at $t = 0$:
- $$y(t = 0 ) = 1\hspace{0.05cm}{\rm V}\cdot \int_{ - 1\,{\rm ms} }^{ 1\,{\rm ms} } {k \hspace{0.1cm}}{\rm d}\tau = 1\hspace{0.05cm}{\rm V}\cdot \int_{ - 1\,{\rm ms} }^{ 1\,{\rm ms} } {\frac{1}{2\,{\rm ms}} \hspace{0.1cm}}{\rm d}\tau= 1\hspace{0.05cm}{\rm V}.$$
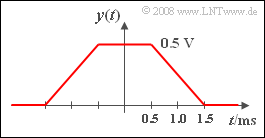
(3) Approach 3 is correct:
- Convolution of two rectangles of different widths results in the trapezoidal output signal as shown in the sketch.
- The maximum value occurs in the constant range from $-0.5 \hspace{0.05cm} \rm ms$ to $+0.5 \hspace{0.05cm} \rm ms$ and is
- $$y(t = 0 ) = 1\hspace{0.05cm}{\rm V} \cdot \frac{1}{2\,{\rm ms}} \hspace{0.05cm}\cdot 1\,{\rm ms} = 0.5\hspace{0.05cm}{\rm V}.$$
(4) Approaches 2, 3 and 4 are correct:
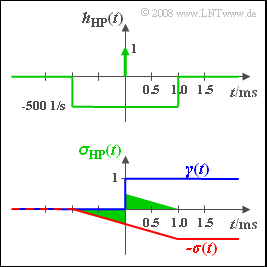
- The impulse response of the total system is: $h_{\rm HP}(t) = \delta(t) - h(t).$ Both parts are shown in the sketch.
- The searched-for signal $z(t)$ is obtained via integration over $h_{\rm HP}(t)$ and multiplication by $1 \hspace{0.05cm} \rm V$ .
In the below sketch are shown:
- the integral over $δ(t)$ blue,
- the function $-σ(t)$ red, and
- the entire signal $z(t)$ green.
- $z(t)$ is an odd function in $t$ with a jump discontinuity at $t = 0$: The signal value at $t = 0$ is exactly halfway between the left– and the right-hand limit and is therefore zero.
- For $t > 1 \hspace{0.05cm} \rm ms$ , $z(t) = 0$ holds, too, since the overall system has a high-pass characteristic.
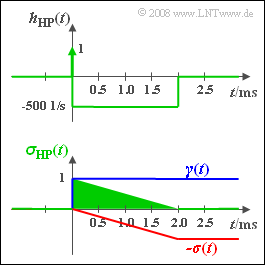
(5) The bottom graph shows the resulting impulse response $h_{\rm HP}(t)$ and the step response $σ_{\rm HP}(t)$.
- The latter jumps at $t = 0$ to the value $1$ and decays to the final value of "zero" until time $t = 2 \hspace{0.05cm} \rm ms$ .
- At time $t = 1\ \rm ms$ , the following is obtained: $σ_{\rm HP}(t) = 0.5$.
- The signal $z(t)$ is identical in shape to the step response $σ_{\rm HP}(t)$ but is yet to be multiplied by $1 \hspace{0.05cm} \rm V$ .
- The searched-for signal value at time $t_1 = 1 \hspace{0.05cm} \rm ms$ thus results in $z(t_1) \; \rm \underline{ = \ 0.5 \: {\rm V}}$.