Exercise 2.2Z: Power Consideration
From LNTwww
Let us consider two harmonic oscillations
- $$ s_1(t) = A_1 \cdot \cos(\omega_{\rm 1} \cdot t ) \hspace{0.05cm},$$
- $$s_2(t) = A_2 \cdot \cos(\omega_{\rm 2} \cdot t + \phi) \hspace{0.05cm},$$
where $f_2 ≥ f_1$ should hold for the frequencies.
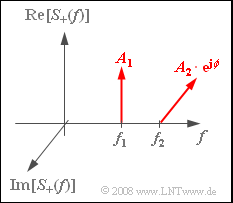
- The graph on the right shows the spectrum of the analytical signal $s_+(t)$, which is additively composed of the two components $s_{1+}(t)$ and $s_ {2+}(t)$ .
- Here, the transmission power $P_{\rm S}$ should be understood as the second order moment of the signal $s(t)$, averaged over the largest measurement period possible:
- $$P_{\rm S} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {s^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- According to this definition: If $s(t)$ describes a voltage waveform, $P_{\rm S}$ has unit $\rm V^2$ and refers to resistance $R = 1 \ \rm Ω$.
- Dividing by $R$ gives the physical power in $\rm W$.
Hints:
- This exercise belongs to the chapter Double-Sideband Amplitude Modulation.
- Reference is also made to the chapter Quality Criteria.
- Use the numerical values $A_1 = 2\ \rm V$, $A_2 = 1 \ \rm V$, and $R = 50 \ \rm Ω$.
Questions
Solution
(1) According to the equations specified on the exercise page:
- $$P_{\rm 1} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {A_1^2 \cdot \cos^2(\omega_{\rm 1} t + \phi_1) }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- For more general calculation, we consider the phase $ϕ_1$, which is actually zero here. Using the equation $\cos^{2}(α) = 0.5 · (1 + \cos(2α))$, we get:
- $$ P_{\rm 1} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {\frac{A_1^2}{2}}\hspace{0.1cm}{\rm d}t + \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {\frac{A_1^2}{2}\cdot \cos(2\omega_{\rm 1} t + 2\phi_1)}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}.$$
- Regardless of the phase $ϕ_1$, the second term does not contribute to the division by $T_{\rm M}$ and subsequent boundary transition due to integration over the cosine function. Thus, we get:
- $$P_{\rm 1} = \frac{A_1^2}{2} = \frac{(2\,{\rm V})^2}{2} \hspace{0.15cm}\underline {= 2\,{\rm V}^2}\hspace{0.05cm}.$$
(2) With $R = 50\ \rm Ω$, we get the "unnormalized" power:
- $$P_{\rm 1} = \frac{2\,{\rm V}^2}{50\,{\rm \Omega}} \hspace{0.15cm}\underline {= 40\,{\rm mW}}\hspace{0.05cm}.$$
(3) It has already been shown in the solution to subtask (1) that the phase has no influence on the power. It follows that:
- $$P_{\rm 2} = \frac{A_2^2}{2} \hspace{0.15cm}\underline {= 0.5\,{\rm V}^2}\hspace{0.05cm}.$$
(4) To calculate this power, we have to average over $s^{2}(t)$, where:
- $$s^2(t) = s_1^2(t) + s_2^2(t) + 2 \cdot s_1(t) \cdot s_2(t).$$
- Due to the division by the measurement duration $T_{\rm M}$ and the required boundary transition, the last term does not contribute regardless of the phase $ϕ$ . Thus:
- $$P_{\rm S} = P_{\rm 1} + P_{\rm 2} \hspace{0.15cm}\underline {= 2.5\,{\rm V}^2}\hspace{0.05cm}.$$
(5) When $f_2 = f_1$, the spectrum of the analytical signal is:
- $$S_+(f) = (A_{\rm 1} + A_{\rm 2} \cdot {\rm e}^{{\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm} \phi})\cdot \delta (f - f_1) \hspace{0.05cm}.$$
- This results in the signal:
- $$s(t) = A_3 \cdot \cos(\omega_{\rm 1} t + \phi_3) \hspace{0.05cm},$$
- whose phase $ϕ_3$ does not matter for the power calculation. The amplitude of this signal is
- $$A_3 = \sqrt{ \left(A_1 + A_2 \cdot \cos(\phi)\right)^2 + A_2^2 \cdot \sin^2(\phi)} = \sqrt{ A_1^2 + A_2^2 + 2 \cdot A_1 \cdot A_2 \cdot \cos(\phi)}\hspace{0.05cm}.$$
- For $ϕ = 0$, the sum of the amplitudes is scalar:
- $$A_3 = \sqrt{ A_1^2 + A_2^2 + 2 \cdot A_1 \cdot A_2 } = A_1 + A_2 = 3\,{\rm V}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm S} \hspace{0.15cm}\underline {= 4.5\,{\rm V}^2}\hspace{0.05cm}.$$
- On the other hand, the amplitudes for $ϕ = 90^\circ$ are added as vectors ⇒ same result as in subtask (4):
- $$ A_3 = \sqrt{ A_1^2 + A_2^2 } = \sqrt{5}\,{\rm V}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm S} = \frac{5\,{\rm V}^2}{2}\hspace{0.15cm}\underline {= 2.5\,{\rm V}^2}\hspace{0.05cm}.$$
- For $ϕ = 180^\circ$, the cosine oscillations overlap destructively:
- $$A_3 = A_1 - A_2 = 1\,{\rm V}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm S} \hspace{0.15cm}\underline {= 0.5\,{\rm V}^2}\hspace{0.05cm}.$$