Exercise 2.3Z: About the LZ77 Coding
In Exercise 2.3, you were supposed to compress "BARBARA–BAR" (string of length $11$, four different characters) using the LZ78 algorithm.
In this exercise we use the same text to demonstrate LZ77 compression. To note:
- While the successor "LZ78" successively builds a global dictionary, "LZ77" uses a local dictionary.
- The LZ77 method works with a "Sliding Window" that is gradually shifted over the input text.
- This "sliding window" is divided into the "preview buffer" (highlighted in blue in the graphic) and the "search buffer" (highlighted in red). Both buffers have a size of $G$ memory locations each.
- Each coding step $i$ is characterised by a triple $(P,\ L,\ Z)$. Here, $P$ and $L$ are integers and $Z$ is a character. Transmitted are the binary representations of $P$, $L$ and $Z$.
- After transmission, the sliding window is shifted one or more positions to the right and the next coding step $i + 1$ begins.
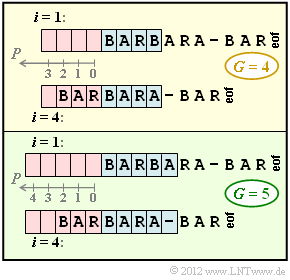
The upper diagram shows the initial allocation with the buffer size $G = 4$ at the times $i = 1$ as well as $i = 4$.
- At time $i = 1$ , the search buffer is empty, so the coder output is $(0, 0,$ B$)$ .
- After the shift by one position, the search buffer contains a B, but no string that begins with A. The second number triple is therefore $(0, 0,$ A$)$.
- The output for $i = 3$ is $(0, 0,$ R$)$, since there is no string beginning with R in the search buffer even now.
The snapshot at time $i = 4$ is also shown in the graphic. The search is now for the character string in the search buffer that best matches the preview text BARA . A number triple $(P,\ L,\ Z)$, is transmitted again, but now with the following meaning:
- $P$ indicates the position in the (red) search buffer where the match starts. The $P$ values of the individual memory locations can be seen in the graphic.
- $L$ denotes the number of characters in the search buffer that, starting at $P$, match the current string in the preview buffer.
- Finally $Z$ denotes the first character in the preview buffer that differs from the matching string found in the search buffer.
The larger the LZ77 parameter $G$ , the easier it is to find the longest possible match. In subtask (4) you will notice that the LZ77 encoding with $G = 5$ gives a better result than the one with $G = 4$.
- However, because of the later binary representation of $P$, one will always choose $G$ as a power of two, so that $G$ can be represented with $\log_2 \ P$ bits $(G = 8$ ⇒ three-digit binary number $P)$.
- This means that a "Sliding Window" with $G = 5$ has rather little practical relevance.
Hints:
- The task belongs to the chapter Compression according to Lempel, Ziv and Welch.
- In particular, reference is made to the page LZ77 – the basic form of the Lempel-Ziv algorithms .
- The original literature [LZ77] on this method is:
Ziv, J.; Lempel, A.: A Universal Algorithm for Sequential Data Compression. In: IEEE Transactions on Information Theory, no. 3, vol. 23, 1977, p. 337–343.
- Exercise 2.3 and Exercise 2.4 deal with other Lempel–Ziv methods in a similar way.
Questions
Solution
(1) Solution suggestion 3 is correct.
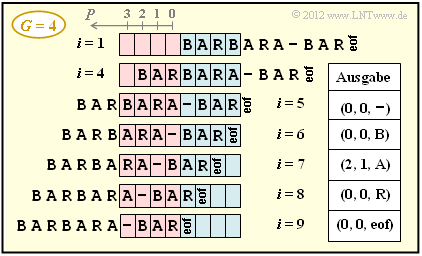
- The preview buffer contains the character string "BARA" at the time $i = 4$ .
- The search buffer contains "BAR" in the last three digits:
- $$P = 2\hspace{0.05cm},\hspace{0.2cm}L = 3\hspace{0.05cm},\hspace{0.2cm}Z = \boldsymbol{\rm A}\hspace{0.05cm}.$$
(2) The first two solutions are correct:
- The hyphen is not found in the search buffer at time $i = 5$.
- The output is $(0, 0,$ –$)$.
(3) The upper graphic shows the "Sliding Window" and the coder output at times $i>5$.
- After $i = 9$ coding steps the coding process is finished considering eof ⇒ $\underline{i_{\rm end} = 9}$.
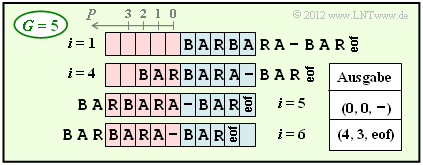
(4) With a larger buffer size $(G = 5$ instead of $G = 4)$ the coding is already completed after the 6th coding step ⇒ $\underline{i_{\rm end} = 6}$.
- A comparison of the two graphs shows that nothing changes for $G = 5$ compared to $G = 4$ up to and including $i = 5$ .
- Due to the larger buffer, however, "BAR" can now be coded together with "eof" (end-of-file) in a single step, whereas with $G = 4$ four steps were necessary for this.
(5) Only statement 1 is correct.
- A disadvantage of LZ77 is the local dictionary. Phrases that are actually already known cannot be used for data compression if they occurred more than $G$ characters earlier in the text. In contrast, with LZ78 all phrases are stored in the global dictionary.
- It is true that with LZ78 only pairs $(I, \ Z)$ have to be transmitted, whereas with LZ77 each coding step is identified by a triple $(P, \ L, \ Z)$ . However, this does not mean that fewer bits have to be transmitted per coding step.
- Consider, for example, the buffer size $G = 8$. With LZ77, one must then represent $P$ with three bits and $L$ with four bits. Please note that the match found between the preview buffer and the search buffer may also end in the preview buffer.
- The new character $Z$ requires exactly the same number of bits in LZ78 as in LZ77 (namely two bits), if one assumes the symbol set size $M = 4$ as here.
- Statement 2 would only be correct if $N_{\rm I}$ were smaller than $N_{\rm P}+ N_{\rm L}$, for example $N_{\rm I} = 6$. But this would mean that one would have to limit the dictionary size to $I = 2^6 = 64$ . This is not sufficient for large files.
- Our rough calculation, however, is based on a uniform number of bits for the index $I$. With a variable number of bits for the index, you can save quite a few bits by transmitting $I$ only with as many bits as are necessary for the coding step $i$ .
- In principle, however, this does not change the limitation of the dictionary size, which will always lead to problems with large files.