Contents
- 1 Static and dynamic dictionary techniques
- 2 LZ77 - the basic form of the Lempel-Ziv algorithms
- 3 The Lempel-Ziv variant LZ78
- 4 The Lempel-Ziv-Welch algorithm
- 5 Lempel-Ziv coding with variable index bit length
- 6 Decoding of the LZW algorithm
- 7 Remaining redundancy as a measure for the efficiency of coding methods
- 8 Efficiency of Lempel-Ziv coding
- 9 Quantitative statements on asymptotic optimality
- 10 Exercises for the chapter
Static and dynamic dictionary techniques
Many data compression methods use dictionaries. The idea is the following:
- Construct a list of character patterns that occur in the text,
- and encode these patterns as indices of the list.
This procedure is particularly efficient if certain patterns are repeated frequently in the text and if this is also taken into account in the coding. A distinction is made here between
- procedures with static dictionary,
- procedures with dynamic dictionary.
$\text{(1) Procedures with static dictionary}$
A static dictionary is only useful for very special applications, for example for a file of the following form:
For example, the assignments result in
- $$"\boldsymbol{\rm 0}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 000000} \hspace{0.05cm},\hspace{0.15cm} ... \hspace{0.15cm},\hspace{0.05cm} "\boldsymbol{\rm 9}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 001001} \hspace{0.05cm}, "\hspace{-0.03cm}\_\hspace{-0.03cm}\_\hspace{0.03cm}" \hspace{0.1cm}{\rm (blank)}\hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 001010} \hspace{0.05cm},$$
- $$"\hspace{-0.01cm}.\hspace{-0.01cm}" \hspace{0.1cm}{\rm (point)}\hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 001011} \hspace{0.05cm}, "\hspace{-0.01cm},\hspace{-0.01cm}" \hspace{0.1cm}{\rm (comma)}\hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 001011} \hspace{0.05cm}, " {\rm end\hspace{-0.1cm}-\hspace{-0.1cm}of\hspace{-0.1cm}-\hspace{-0.1cm}line}\hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 001101} \hspace{0.05cm},$$
- $$"\boldsymbol{\rm A}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 100000} \hspace{0.05cm},\hspace{0.15cm} ... \hspace{0.15cm},\hspace{0.05cm} "\boldsymbol{\rm E}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 100100} \hspace{0.05cm}, \hspace{0.15cm} ... \hspace{0.15cm},\hspace{0.05cm} "\boldsymbol{\rm L}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 101011} \hspace{0.05cm},\hspace{0.15cm}"\boldsymbol{\rm M}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 101100} \hspace{0.05cm},$$
- $$"\boldsymbol{\rm O}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 101110} \hspace{0.05cm},\hspace{0.15cm} ... \hspace{0.15cm},\hspace{0.05cm} "\boldsymbol{\rm U}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 110100} \hspace{0.05cm}, "\boldsymbol{\rm Name\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 010000} \hspace{0.05cm},\hspace{0.05cm}$$
- $$"\boldsymbol{\rm ,\_\hspace{-0.03cm}\_Vorname\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 010001} \hspace{0.05cm},\hspace{0.05cm} "\boldsymbol{\rm ,\_\hspace{-0.03cm}\_Wohnort\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 010010} \hspace{0.05cm},\hspace{0.15cm} ... \hspace{0.15cm}$$
for the first line of the above text, binary source coded with six bits per character:
- $$\boldsymbol{010000} \hspace{0.15cm}\boldsymbol{100000} \hspace{0.15cm}\boldsymbol{100001} \hspace{0.15cm}\boldsymbol{100100} \hspace{0.15cm}\boldsymbol{101011} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \boldsymbol{(\rm Name\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_) \hspace{0.05cm}(A)\hspace{0.05cm}(B)\hspace{0.05cm}(E)\hspace{0.05cm}(L)}$$
- $$\boldsymbol{010001} \hspace{0.15cm}\boldsymbol{101011}\hspace{0.15cm} \boldsymbol{100100} \hspace{0.15cm}\boldsymbol{101110} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \boldsymbol{(,\hspace{-0.05cm}\_\hspace{-0.03cm}\_\rm Vorname\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_) \hspace{0.05cm}(L)\hspace{0.05cm}(E)\hspace{0.05cm}(O)}$$
- $$\boldsymbol{010010} \hspace{0.15cm}\boldsymbol{110100} \hspace{0.15cm}\boldsymbol{101011} \hspace{0.15cm}\boldsymbol{101100} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \boldsymbol{(,\hspace{-0.05cm}\_\hspace{-0.03cm}\_\rm Wohnort\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_) \hspace{0.05cm}(U)\hspace{0.05cm}(L)\hspace{0.05cm}(M)} \hspace{0.05cm} $$
- $$\boldsymbol{001101} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ({\rm end\hspace{-0.1cm}-\hspace{-0.1cm}of\hspace{-0.1cm}-\hspace{-0.1cm}line}) \hspace{0.05cm}$$
$\text{Conclusion:}$
In this specific application the first line can be displayed with $14 \cdot 6 = 84$ bits.
- In contrast, conventional binary coding would require $39 \cdot 7 = 273$ bits
(because of the lowercase letters in the text, six bits per character are not sufficient here). - For the entire text, this results in $103 \cdot 6 = 618$ bits versus $196 \cdot 7 = 1372$ bits.
- However, the code table must also be known to the recipient.
$\text{(2) Procedures with dynamic dictionary}$
Nevertheless, all relevant compression methods do not work with static dictionaries, but with »dynamic dictionaries«, which are created successively only during the coding:
- Such procedures are flexible and do not have to be adapted to the application. One speaks of »universal source coding procedures«.
- A single pass is sufficient, whereas with a static dictionary the file must first be analyzed before the encoding process.
- At the sink, the dynamic dictionary is generated in the same way as for the source. This eliminates the need to transfer the dictionary.
$\text{Example 1:}$ The graphic shows a small section of $80$ byte of a $\text{BMP file}$ in hexadecimal format. It is the uncompressed representation of a natural picture.
- You can see that in this small section of a landscape image the bytes $\rm FF$, $\rm 55$ and $\rm 47$ occur very frequently. Data compression is therefore promising.
- But since other parts of the file or other byte combinations dominate in other image contents, the use of a static dictionary would not be appropriate here.
$\text{Example 2:}$ For an artificially created graphic, for example a form, you could work with a static dictionary.
We are looking at a "black & white" image with $27 × 27$ pixels, where the mapping "black" ⇒ 0 and "white" ⇒ 1 has been agreed upon.
- At the top (black marker), each line is described by $27$ zeros.
- In the middle (blue marker), three zeros and three ones always alternate.
- At the bottom (red marker), 25 ones per line are limited by two zeros.
LZ77 - the basic form of the Lempel-Ziv algorithms
The most important procedures for data compression with a dynamic dictionary go back to $\text{Abraham Lempel}$ and $\text{Jacob Ziv}$. The entire Lempel-Ziv family (in the following we will use for this briefly: $\rm LZ$ procedure) can be characterized as follows:
- Lempel-Ziv methods use the fact that often whole words, or at least parts of them, occur several times in a text. One collects all word fragments, which are also called "phrases" in a sufficiently large dictionary.
- Contrary to the entropy coding developed some years before (by Shannon and Huffman), the frequency of single characters or character strings is not the basis of the compression here, so that the LZ procedures can be applied even without knowledge of the source statistics.
- LZ compression accordingly manages with a single pass and also the source symbol set size $M$ and the symbol set $\{q_μ\}$ with $μ = 1$, ... , $M$ does not have to be known. This is called »Universal Source Coding«.
We first look at the Lempel-Ziv algorithm in its original form from 1977, known as $\rm LZ77$:
- This works with a window that is successively moved over the text ⇒ one also speaks of a "sliding window".
- The window size $G$ is an important parameter that decisively influences the compression result.
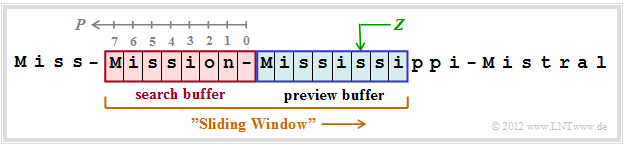
The graphic shows an example of the sliding windows. This is divided into
- the "preview buffer" $($blue background), and
- the "search buffer" $($red background, with the positions
$P = 0$, ... , $7$ ⇒ window size $G = 8)$.
The text consists of the words Miss, Mission, Mississippi and Mistral, each separated by a hyphen. At the time under consideration the preview buffer contains Mississi.
- Search now in the search buffer for the best match ⇒ the string with the maximum match length $L$. This is the result for position $P = 7$ and length $L = 5$ to Missi.
- This step is expressed by the triple $(7, 5, $ s$)$ ⇒ general $(P, \ L, \ Z)$, where $Z =$ s specifies the character that no longer matches the string found in the search buffer.
- At the end the window is moved by $L + 1 = 6$ character is moved to the right. In the preview buffer there is now sippi-Mi, and in the search buffer n-Missis.
The encoding gives the triple $(2, 2,$ p$)$.
In the following example the LZ77 coding algorithm is described in more detail. The decoding runs in a similar way.
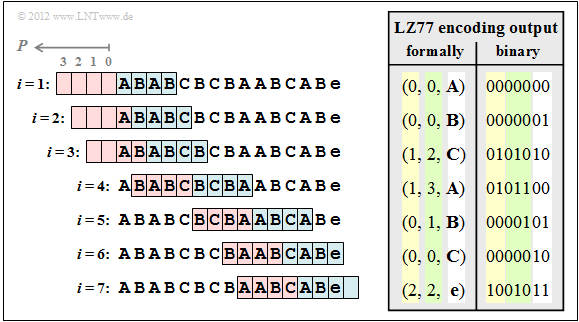
$\text{Example 3:}$ We consider the LZ77 encoding of the string ABABCBCBAABCABe according to the following graphic. The input sequence has the length $N = 15$.
Further is assumed:
- For the characters apply $Z ∈ \{$ A, B, C, e $\}$, where e corresponds to the "end-of-file" (end of the input string)
- The size of the preview and search buffer are $G = 4$ ⇒ position $P ∈ \{0, 1, 2, 3\}$.
Display of the encoding process:
Step 1 and 2: The characters A and B are encoded by the triple $(0, 0, $ A$)$ and $(0, 0, $ B$)$, because they are not yet stored in the search buffer. Then move the sliding window by 1.
Step 3: AB is masked by the search buffer and at the same time the still unknown character C is appended. After that the sliding window is moved three positions to the right.
Step 4: This shows that the search string BCB may also end in the preview buffer. Now the window can be moved four positions to the right.
Step 5: Only A is found in the search buffer and B is dropped. If the search buffer is larger, however, ABC could be masked together. For this purpose must be $G ≥ 7$.
Step 6: Likewise, the character C must be coded separately due to the buffer being too small. But since CA hasn't occurred before, $G = 7$ would not improve the compression here.
Step 7: With the consideration of the end-of-file (e) together with AB from the search buffer, the encoding process is finished.
Before transmission, the specified triples must of course be binary coded. In this example
- the position $P ∈ \{0,\ 1,\ 2,\ 3\}$ needs two bits (yellow background in the table above),
- the copy length $L$ needs three bits (green background), so that also $L = 7$ could still be displayed,
- all characters need two bits (white background), for example A → 00, B → 01, C → 10, e ("end-of-file") → 11.
Thus the $\rm LZ77$ output sequence has a length of $7 \cdot 7 = 49$ bits, while the input sequence only needed $15 \cdot 2 = 30$ bits.
$\text{Conclusion:}$ Lempel-Ziv compression only makes sense with large files !
The Lempel-Ziv variant LZ78
The LZ77 algorithm produces very inefficient output if more frequent strings are repeated only with a larger distance. Such repetitions can often not be recognized due to the limited buffer size $G$ of the sliding window.
Lempel and Ziv corrected this shortcoming already one year after the release of the first version LZ77:
- The algorithm $\rm LZ78$ uses a global dictionary for compression instead of the local dictionary (search buffer).
- The size of the dictionary allows efficient compression of phrases that have been used for a long time before.
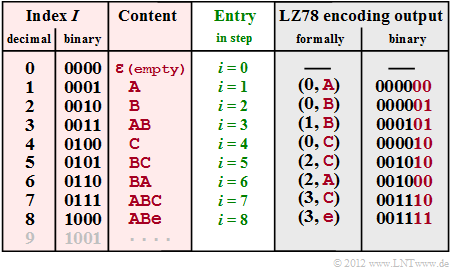
$\text{Example 4:}$ To explain the LZ78 algorithm we consider the same sequence ABABCBCBAABCABe as for the LZ77 $\text{Example 3}$.
The graphic shows (with red background) the dictionary
- with index $I $ (in decimal and binary representation, column 1 and 2)
- and the corresponding content (column 3),
- which is entered for coding step $i $ (column 4). For LZ78 both encoding and decoding are always $i = I$.
- In column 5 you find the formalized code output $($Index $I$, new character $Z)$.
- In column 6 the corresponding binary coding is given with four bits for the index and the same character assignment A → 00, B → 01, C → 10, e ("end-of-file") → 11 as in $\text{Example 3}$.
- At the beginning (step $\underline{i = 0}$) the dictionary is (WB) empty except for the entry ε $($empty character, not to be confused with the space character, which is not used here$)$ with index $I = 0$.
- In the step $\underline{i = 1}$ there is no usable entry in the dictionary yet, and it becomes (0, A) output (A follows ε). In the dictionary, the entry A follows in line $I = 1$ (abbreviated 1: A).
- The procedure in the second step ($\underline{i = 2}$). The output is (0, B) and the dictionary entry is 2: B .
- As the entry $\underline{i = 3}$ is already found in step 1: A , the characters AB can be coded together by (1, B) and the new dictionary entry 3: AB is made.
- After coding and insertion of the new character C in step $\underline{i = 4}$ the pair of characters BC is coded together ⇒ (2, C) and entered into the dictionary 5: BC in step $\underline{i = 5}$ .
- In step $\underline{i = 6}$ two characters are treated together with '6: BA and in the last two steps three each, namely 7: ABC and 8: ABe.
- The output (3, C) in step $\underline{i = 7}$ stands for "WB(3) + C = ABC and the output (3, e) in step $\underline{i = 8}$ for ABe.
In this $\text{Example 4}$ the LZ78 encoded sequence thus consists of $8 - 6 = 48$ bit. The result is comparable to the LZ77-$\text{Example 3}$ $(49$ bit$)$.
$\text{Conclusion:}$ Details and improvements of LZ78 will be omitted here. Here we refer to the $\text{LZW algorithm}$, which will be described in the following sections. Only this much will be said now:
- The index $I$ is uniformly represented here with four bits, whereby the dictionary is limited to $16$ entries. By a "variable number of bits" for the index one can bypass this limitation. At the same time one gets a better compression factor.
- The dictionary does not have to be transmitted with all LZ variants, but is generated with the decoder in exactly the same way as on the encoder side. The decoding is also done with LZ78, but not with LZW, in the same way as the encoding.
- All LZ procedures are asymptotically optimal, i.e., for infinitely long sequences the mean code word length $L_{\rm M}$ per source symbol is equal to the source entropy $H$.
- For short sequences, however, the deviation is considerable. More about this at the "end of chapter".
The Lempel-Ziv-Welch algorithm
The most common variant of Lempel-Ziv compression used today was designed by $\text{Terry Welch}$ and published in 1983. In the following we refer to it as the "Lempel-Ziv-Welch-Algorithm", abbreviated as $\rm LZW$. Just as LZ78 has slight advantages over LZ77 (as expected, why else would the algorithm have been modified?), LZW also has more advantages than disadvantages compared to LZ78.
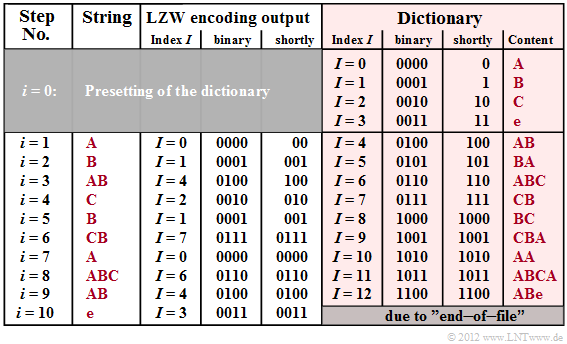
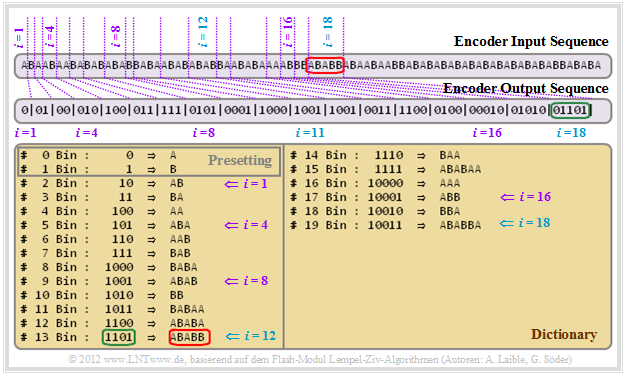
The graphic shows the coder output for the exemplary input sequence ABABCBCBAABCABe. On the right you can see the dictionary (highlighted in red), which is successively generated during LZW encoding. The differences to LZ78 can be seen in comparison to the graphic in the last section, namely:
- For LZW, all characters occurring in the text are already entered at the beginning $(i = 0)$ and assigned to a binary sequence, in the example with the indices $I = 0$, ... , $I = 3$.
- This also means that LZW requires some knowledge of the message source, whereas LZ78 is a "true universal encoding".
- For LZW, only the dictionary index $I$ is transmitted for each encoding step $i$ while for LZ78 the output is the combination $(I$, $Z)$, where $Z$ denotes the current new character.
- Due to the absence of $Z$ in the encoder output, LZW decoding is more complicated than with LZ78, as described in section "Decoding of the LZW algorithm".
$\text{Example 5:}$ For this exemplary $\rm LZW$ encoding, again the input sequence ABABCBCBAABCABe is assumed as with "LZ77" and "LZ78". So the following description refers to the above graphic.
Step i = 0 (default): The allowed characters A, B, C and e ("end-of-file") are entered into the dictionary and assigned to the indices $I = 0$, ... , $I = 3$ .
Step i = 1: The character A is encoded by the decimal index $I = 0$ and its binary representation 0000 is transmitted.
Then the combination of the current character A and the following character B of the input sequence is stored in the dictionary under the index $I = 4$ .
step i = 2: Representation of B by index $I = 1$ or 0001 (binary) as well as dictionary entry of BA placed under index $I = 5$.
Step i = 3: Because of the entry AB at time $i = 1$ the index to be transmitted is $I = 4$ (binary: 0100). New dictionary entry of ABC under $I = 6$.
Step i = 8: Here the characters ABC are represented together by the index $I = 6$ (binary: 0110) and the entry for ABCA is made.
With the encoding of e (EOF mark) the encoding process is finished after ten steps. With LZ78 only eight steps were needed. But it has to be considered:
- The LZW algorithm needs only $10 \cdot 4 = 40$ bit versus the $8 \cdot 6 = 48$ bit for LZ78. Provided that for this simple calculation, four bits each are needed for index representation.
- LZW as well as LZ78 require less bits $($namely $34$ or $42)$, if one considers that for the step $i = 1$ the index has to be encoded with two bits only $(I ≤ 3)$ and for $2 ≤ i ≤ 5$ three bits are sufficient $(I ≤ 7)$.
Lempel-Ziv coding with variable index bit length
For reasons of a most compact representation, we now consider only binary sources with symbol set $\{$A, B$\}$. The terminating character »end-of-file« is not considered, too.
We demonstrate the LZW encoding by means of a screenshot of our interactive SWF module "Lempel-Ziv-Welch algorithms".
- In the first encoding step $(i = 1)$: A ⇒ 0. Afterwards the entry with index $I = 2$ and content AB.
- As there are only two dictionary entries in step $i = 1$ (for A and B ) one bit is sufficient. For step $i = 2$ and $i = 3$ $($B ⇒ 01 and A ⇒ 00$)$ two bits are needed in each case.
- Starting on $i = 4$ , the index representation is done with three bits, then from $i = 8$ with four bits and from $i = 16$ with five bits. A simple algorithm for the respective index bit number $L(i)$ can be derived.
- Let's finally consider the encoding step $i = 18$. Here, the sequence ABABB marked in red, which was entered into the dictionary at time $i = 12$ at time $($Index $I = 13$ ⇒ 1101$)$ is edited. However, the encoder output is now 01101 because of $i ≥ 16$ (green mark at the encoder output).
The statements also apply to $\text{LZ78}$. That is: With LZ78 a variable index bit length results in the same improvement as with LZW.
Decoding of the LZW algorithm
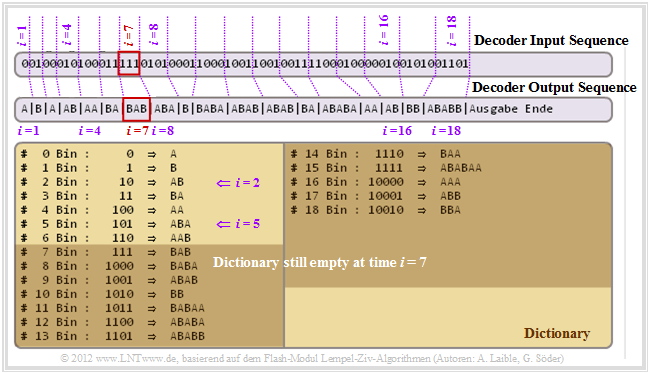
The decoder now displays the decoded output in the "last section" as input sequence. The graphic shows that it is possible to uniquely decode this sequence even with variable index bit lengths. Please note:
- The decoder knows that in the first encoding step $(i = 1)$ the index $I $ was encoded with only one bit, in the steps $i = 2$ and $i = 3$ with two bit, from $i = 4$ with three bit, from $i = 8$ with four bit, and so on.
- The decoder generates the same dictionary as the encoder, but the dictionary entries are made one time step later.
- At step $\underline{i = 1}$ the adjacent symbol 0 is decoded as A. Likewise, the following results for step $\underline{i = 2}$ from the preassignment of the dictionary and the two-bit representation agreed upon for this: 01 ⇒ B.
- The entry of the line $\underline{I = 2}$ $($content: AB$)$ of the dictionary is therefore only made at the step $\underline{i = 2}$, while at the $\text{encoding process}$ this could already be done at the end of step $i = 1$.
- Let us now consider the decoding for $\underline{i = 4}$. The index $\underline{I = 2}$ returns the decoding result 010 ⇒ AB and in the next step $(\underline{i = 5})$ the dictionary line $\underline{I = 5}$ will be filled with ABA.
- This time difference with respect to the dictionary entries can lead to decoding problems. For example, for step $\underline{i = 7}$ there is no dictionary entry with index $\underline{I= 7}$.
- What is to do in such a case as $(\underline{I = i})$? In this case you take the result of the previous decoding step $($here: BA for $\underline{i = 6})$ and append the first character of this sequence at the end again. This gives the decoding result for $\underline{i = 7}$ to 111 ⇒ BAB.
- Naturally, it is unsatisfactory to specify only one recipe. In the "Exercise 2.4Z" you should justify the procedure demonstrated here. We refer to the sample solution for this exercise.
With LZ78 decoding, the problem described here does not occur because not only the index $I $ but also the current character $Z$ is included in the encoding result and is transmitted.
Remaining redundancy as a measure for the efficiency of coding methods
For the rest of this chapter we assume the following prerequisites:
- The source symbol set size $($or in the transmission sense: the number of levels ) is $M$, where $M$ represents a power of two ⇒ $M = 2, \ 4, \ 8, \ 16$, ....
- The source entropy is $H$. If there are no correlations between the symbols and if they are equally probable, then $H = H_0 = \log_2 \ M$. Otherwise, $H < H_0$ applies.
- A symbol sequence of length $N$ is source-coded and returns a binary encoded sequence of length $L$.
- For the time being we do not make any statement about the type of source coding.
According to the $\text{Source Coding Theorem}$ the average code word length $L_{\rm M}$ must be greater than or equal to the source entropy $H$ (in bit/source symbol). This means
- for the total length of the source-coded binary sequence:
- $$L \ge N \cdot H \hspace{0.05cm},$$
- for the relative redundancy of the coded sequence, in the following called »residual redundancy«:
- $$r = \frac{L - N \cdot H}{L} \hspace{0.05cm}.$$
$\text{Example 6:}$ If there were a "perfect source coding" for a redundancy-free binary source sequence $(M = 2,\ p_{\rm A} = p_{\rm B} = 0.5$, without memory$)$ of length $N = 10000$, the encoder sequence would have also the length $L = 10000$.
Consequence: If in a code the result $L = N$ is never possible, then this code is called "not–perfect".
- Lempel-Ziv is not suitable for this redundancy-free message source. It will always be $L > N$. You can also put it quite succinctly like this: The perfect source coding here is "no coding at all".
- A redundant binary source with $p_{\rm A} = 0.89$, $p_{\rm B} = 0.11$ ⇒ $H = 0.5$ could be represented with a perfect source coding with $L = 5000$, without being able to say what this perfect source coding looks like.
- For a quaternary source, $H > 1 \ \rm (bit/source\ symbol)$ is possible, so that even with perfect source coding there will always be $L > N$. If the source is redundancy-free (no memory, all $M$ symbols equally probable), it has the entropy $H= 2 \ \rm (bit/source\ symbol)$.
For all these examples of perfect source coding, the relative redundancy of the encoded sequence ("residual redundancy") is $r = 0$. That is: The zeros and ones are equally probable and there are no correlations between the individual binary symbols.
The problem is: At finite sequence length $N$ there is no perfect source code !
Efficiency of Lempel-Ziv coding
From the Lempel-Ziv algorithms we know (and can even prove this statement) that they are »asymptotically optimal«.
- This means that the relative redundancy of the encoded sequence (here written as a function of the source symbol sequence length $N$:
- $$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$
- For large $N$ the limit value returns "zero":
- $$\lim_{N \rightarrow \infty}r(N) = 0 \hspace{0.05cm}.$$
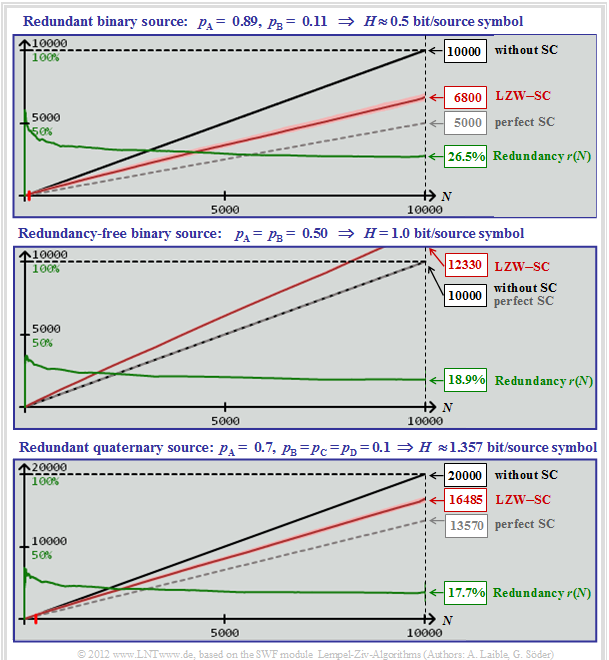
But what does the property "asymptotically optimal" say for practical sequence lengths? Not too much, as the following screenshot of our simulation tool "Lempel-Ziv algorithms" shows. All curves apply exactly only to the $\text{LZW algorithm}$. However, the results for $\text{LZ77}$ and $\text{LZ78}$ are only slightly worse.
The three graphs show for different message sources the dependence of the following sizes on the source symbol sequence length $N$:
- the required number $N \cdot \log_2 M$ of bits without source coding (black curves),
- the required number $H \cdot N$ of bits with perfect source coding (gray dashed),
- the required number $L(N)$ of bits for LZW coding (red curves after averaging),
- the relative redundancy ⇒ residual redundancy $r(N)$ in case of LZW coding (green curves).
$\underline{\text{Redundant binary source (upper graphic)} }$
- $$M = 2, \hspace{0.1cm}p_{\rm A} = 0.89,\hspace{0.1cm} p_{\rm B} = 0.11$$
- $$\Rightarrow \hspace{0.15cm} H = 0.5 \ \rm bit/source\hspace{0.15cm} symbol\text{:}$$
- The black and gray curves are true straight lines (not only for this parameter set).
- The red curve $L(N)$ is slightly curved (difficult to see with the naked eye).
- Because of this curvature of $L(N)$ the residual redundancy (green curve) drops slightly.
- $$r(N) = 1 - 0.5 \cdot N/L(N).$$
- The numerical values can be read:
- $$L(N = 10000) = 6800,\hspace{0.5cm} r(N = 10000) = 26.5\%.$$
$\underline{\text{Redundancy-free binary source (middle graphic)} }$
- $$M = 2,\hspace{0.1cm} p_{\rm A} = p_{\rm B} = 0.5$$
- $$\Rightarrow \hspace{0.15cm} H = 1 \ \rm bit/source\hspace{0.15cm} symbol\text{:}$$
- Here the gray and the black straight line coincide and the slightly curved red curve lies above it, as expected.
- Although the LZW coding brings a deterioration here, recognizable from the indication $L(N = 10000) = 12330$, the residual redundancy is smaller than in the upper graph:
- $$r(N = 10000) = 18.9\%.$$
$\underline{\text{Redundant quaternary source (lower graphic)} }$
- $$M = 4,\hspace{0.1cm}p_{\rm A} = 0.7,\hspace{0.1cm} p_{\rm B} = p_{\rm C} = p_{\rm D} = 0.1$$
- $$ \Rightarrow \hspace{0.15cm} H \approx 1.357 \ \rm bit/source\hspace{0.15cm} symbol\text{:}$$
- Without source coding, for $N = 10000$ quaternary symbols $20000$ binary symbols (bits) would be required (black curve).
- If source encoding was perfect, this would result in $N \cdot H= 13570$ bits (gray curve).
- With (imperfect) LZW encoding you need $L(N = 10000) ≈ 16485$ bits (red curve).
- The residual redundancy here is $r(N = 10000) ≈17.7\%$ (green curve).
Quantitative statements on asymptotic optimality
The results in the last section have shown that the residual redundancy $r(N = 10000)$ is significantly greater than the theoretically promised value $r(N \to \infty) = 0$.
This practically relevant result shall now be clarified using the example of the redundant binary source with $H = 0.5 \ \rm bit/source\hspace{0.15cm} symbol$ according to the middle graphic in the last section. However, we now consider for the source symbol sequence length values between $N=10^3$ and $N=10^{12}$.
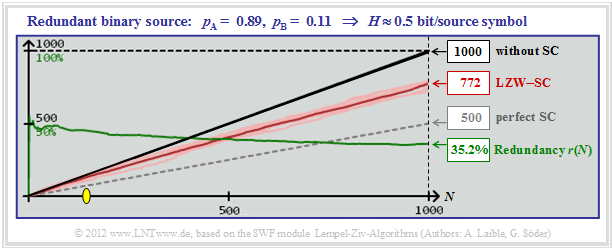
$\text{Example 7:}$ The graphic on the right shows simulation results with only $N = 1000$ binary symbols.
- After averaging over ten series of experiments the result is $r(N = 1000) ≈35.2\%$.
- Below the yellow dot $($in the example with $N ≈ 150)$ the LZW algorithm even brings a deterioration.
- In this range, namely $L > N$, that is: "Red" is above "black".
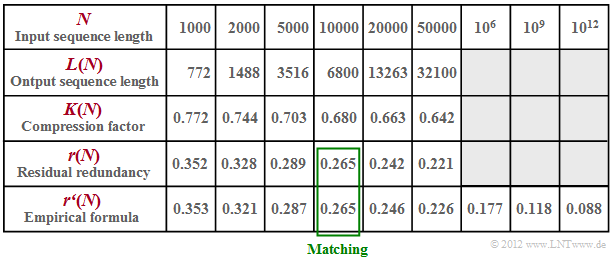
In the table below, the results for this redundant binary source $(H = 0.5)$ are summarized
- The compression factor $K(N)= L(N)/N$ decreases with increasing $N$ only very slowly (line 3).
- In line 4 the residual redundancy $r(N)$ is given for different lengths between $N =1000$ and $N =50000$.
- According to relevant literature this residual redundancy decreases proportionally to $\big[\hspace{0.05cm}\lg(N)\hspace{0.05cm}\big]^{-1}$.
- In line 5 the results of an empirical formula are entered $($adaptation for $N = 10000)$:
- $$r\hspace{0.05cm}'(N) = \frac{A}{ {\rm lg}\hspace{0.1cm}(N)}\hspace{0.5cm}{\rm with}$$
- $$ A = {r(N = 10000)} \cdot { {\rm lg}\hspace{0.1cm}10000} = 0.265 \cdot 4 = 1.06 \hspace{0.05cm}.$$
- You can see the good agreement between our simulation results $r(N)$ and the rule of the thumb $r\hspace{0.05cm}′(N)$.
- You can also see that the residual redundancy of the LZW algorithm for $N = 10^{12}$ is still $8.8\%$ .
- For other sources, with other $A$–values you will get similar results. The principle process remains the same. See also "Exercise 2.5" and "Exercise 2.5Z".
Exercises for the chapter
Exercise 2.3: About the LZ78 Compression
Exercise 2.3Z: To the LZ77 Coding
Exercise 2.4: About the LZW algorithm
Exercise 2.4Z: LZW Coding and Decoding again
Exercise 2.5: Residual Redundancy with LZW Coding
Exercise_2.5Z: Compression Factor vs. Residual Redundancy