Exercise 2.5Z: Multi-Path Scenario
In Exercise 2.5, a delay–Doppler function (or scatter function) was given. From this, you should calculate and interpret the other system functions. The given scatter function $s(\tau_0, f_{\rm D})$ was
- $$s(\tau_0, f_{\rm D}) =\frac{1}{\sqrt{2}} \cdot \delta (\tau_0) \cdot \delta (f_{\rm D} - 100\,{\rm Hz}) \ - \ $$
- $$\hspace{1.5cm} \ - \ \hspace{-0.2cm} \frac{1}{2} \cdot \delta (\tau_0 \hspace{-0.05cm}- \hspace{-0.05cm}1\,{\rm \mu s}) \cdot \delta (f_{\rm D} \hspace{-0.05cm}- \hspace{-0.05cm}50\,{\rm Hz}) \ - \frac{1}{2} \cdot \delta (\tau_0 \hspace{-0.05cm}- \hspace{-0.05cm}1\,{\rm \mu s}) \cdot \delta (f_{\rm D}\hspace{-0.05cm} + \hspace{-0.05cm}50\,{\rm Hz}) \hspace{0.05cm}.$$
Note: In our learning tutorial, $s(\tau_0, \hspace{0.05cm} f_{\rm D})$ is also identified with $\eta_{\rm VD}(\tau_0, \hspace{0.05cm}f_{\rm D})$.
Here we have replaced the delay variable $\tau$ with $\tau_0$ . The new variable $\tau_0$ describes the difference between the delay of a path and the delay $\tau_1$ of the main path. The main path is thus identified in the above equation by $\tau_0 = 0$.
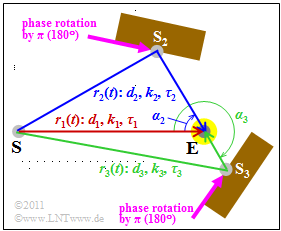
Now, we try to find a mobile radio scenario in which this scatter function would actually occur. The basic structure is sketched above as a top view, and the following hold:
- A single frequency is transmitted: $f_{\rm S} = 2 \ \rm GHz$.
- The mobile receiver $\rm (E)$ is represented here by a yellow dot. It is not known whether the vehicle is stationary, moving towards the transmitter $\rm (S)$ or moving away.
- The signal reaches the receiver via a main path (red) and two secondary paths (blue and green). Reflections from the obstacles cause phase shifts of $\pi$.
- ${\rm S}_2$ and ${\rm S}_3$ are to be understood here as fictitious transmitters from whose position the angles of incidence $\alpha_2$ and $\alpha_3$ of the secondary paths can be determined.
- Let the signal frequency be $f_{\rm S}$, the angle of incidence $\alpha$, the velocity $v$ and the velocity of light $c = 3 \cdot 10^8 \ \rm m/s$. Then, the Doppler frequency is
- $$f_{\rm D}= {v}/{c} \cdot f_{\rm S} \cdot \cos(\alpha) \hspace{0.05cm}.$$
- The damping factors $k_1$, $k_2$ and $k_3$ are inversely proportional to the path lengths $d_1$, $d_2$ and $d_3$. This corresponds to the path loss exponent $\gamma = 2$.
- This means: The signal power decreases quadratically with distance $d$ and accordingly the signal amplitude decreases linearly with $d$.
Notes:
- This task belongs to chapter The GWSSUS Channel Model.
- We also refer to the pages Common path-loss model and Doppler frequency and its distribution.
Questionnaire
Solution
(2) The equation for the Doppler frequency is
- $$f_{\rm D}= \frac{v}{c} \cdot f_{\rm S} \cdot \cos(\alpha) \hspace{0.05cm}.$$
- If the angle of incidence is $\alpha=0$, then the Doppler frequency is
- $$f_{\rm D}=\frac{v}{c}\cdot f_{\rm S}.$$
- In this case the speed of the receiver is
- $$v = \frac{f_{\rm D}}{f_{\rm S}} \cdot c = \frac{10^2\,{\rm Hz}}{2 \cdot 10^9\,{\rm Hz}} \cdot 3 \cdot 10^8\,{\rm m/s} = 15\,{\rm m/s} \hspace{0.1cm} \underline {= 54 \,{\rm km/h}} \hspace{0.05cm}.$$
(3) Solutions 1 and 4 are correct:
- The Doppler frequency $f_{\rm D} = 50 \ \rm Hz$ comes from the blue path, because the receiver moves towards the virtual transmitter ${\rm S}_2$ (i.e., towards the reflection point), although not directly.
- In other words: The movement of the receiver reduces the blue path's length.
- The angle $\alpha_2$ between the direction of movement and the connecting line ${\rm S_2 – E}$ is $60^\circ$:
- $$\cos(\alpha_2) = \frac{f_{\rm D}}{f_{\rm S}} \cdot \frac{c}{v} = \frac{50 \,{\rm Hz}\cdot 3 \cdot 10^8\,{\rm m/s}}{2 \cdot 10^9\,{\rm Hz}\cdot 15\,{\rm m/s}} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \alpha_2 \hspace{0.1cm} \underline {= 60^{\circ} } \hspace{0.05cm}.$$
(4) Statements 1 and 3 are correct: From $f_{\rm D} = \, –50 \ \rm Hz$ follows $\alpha_3 = \alpha_2 ± \pi$ ⇒ $\alpha_3 \ \underline {= 240^\circ}$.
(5) All statements are correct:
- The two Dirac functions at $± 50 \ \ \rm Hz$ have the same delay. We have $\tau_3 = \tau_2 = \tau_1 + \tau_0$.
- From the equality of the delays, however, it follows also $d_3 = d_2$.
- As both paths have the same length, their damping factors are equal, too.
(6) The delay difference is $\tau_0 = 1 \ \rm µ s$, as shown in the equation for $s(\tau_0, f_{\rm D})$. This gives the difference in length:
- $$\Delta d = \tau_0 \cdot c = 10^{–6} {\rm s} \cdot 3 \cdot 10^8 \ \rm m/s \ \ \underline {= 300 \ \ \rm m}.$$
(7) The path loss exponent was assumed to be $\gamma = 2$ for this task.
- Then $k_1 = K/d_1$ and $k_2 = K/d_2$. The constant $K$ is only an auxiliary variable that does not need to be considered further.
- The minus sign takes into account the $180^\circ$ phase rotation on the secondary paths.
- From the weights of the Dirac functions one can read $k_1 = \sqrt{0.5}$ and $k_2 = -0.5$. Therefore:
- $$\frac{d_2}{d_1} = \frac{k_1}{-k_2} = \frac{1/\sqrt{2}}{0.5} = \sqrt{2} \hspace{0.15cm} \underline {= 1.414} \hspace{0.05cm}.$$
(8) From $d_2/d_1 = 2^{-0.5}$ and $\Delta d = d_2 \, - d_1 = 300 \ \rm m$ finally follows:
- $$\sqrt{2} \cdot d_1 - d_1 = 300\,{\rm m} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} d_1 = \frac{300\,{\rm m}}{\sqrt{2} - 1} \hspace{0.15cm} \underline {= 724\,{\rm m}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} d_2 = \sqrt{2} \cdot d_1 \hspace{0.15cm} \underline {= 1024\,{\rm m}} \hspace{0.05cm}. $$