Exercise 3.2: Expected Value Calculations
From LNTwww
We consider the following probability mass functions $\rm (PMF)$:
- $$P_X(X) = \big[1/2,\ 1/8,\ 0,\ 3/8 \big],$$
- $$P_Y(Y) = \big[1/2,\ 1/4,\ 1/4,\ 0 \big],$$
- $$P_U(U) = \big[1/2,\ 1/2 \big],$$
- $$P_V(V) = \big[3/4,\ 1/4\big].$$
For the associated random variables, let:
- $X= \{0,\ 1,\ 2,\ 3\}$, $Y= \{0,\ 1,\ 2,\ 3\}$, $U = \{0,\ 1\}$, $V = \{0, 1\}$.
Often, for such discrete random variables, one must have to calculate different expected values of the form
- $${\rm E} \big [ F(X)\big ] =\hspace{-0.3cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm}\hspace{-0.03cm} {\rm supp} (P_X)} \hspace{-0.1cm} P_{X}(x) \cdot F(x). $$
Here, denote:
- $P_X(X)$ denotes the probability mass function of the discrete random variable $X$.
- The "support" of $P_X$ includes all those realisations $x$ of the random variable $X$ with non-vanishing probability.
- Formally, this can be written as
- $${\rm supp} (P_X) = \{ x: \hspace{0.25cm}x \in X \hspace{0.15cm}\underline{\rm and} \hspace{0.15cm} P_X(x) \ne 0 \} \hspace{0.05cm}.$$
- $F(X)$ is an (arbitrary) real-valued function that can be specified in the entire domain of definition of the random variable $X$ .
In the task, the expected values for various functions $F(X)$ are to be calculated, among others for
- $F(X)= 1/P_X(X)$,
- $F(X)= P_X(X)$,
- $F(X)= - \log_2 \ P_X(X)$.
Hints:
- The exercise belongs to the chapter Some preliminary remarks on two-dimensional random variables.
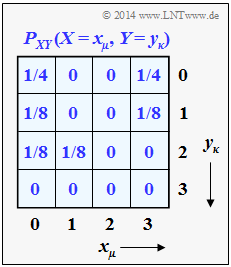
- The two one-dimensional probability mass functions $P_X(X)$ and $P_Y(Y)$ result from the presented 2D–PMF $P_{XY}(X,\ Y)$, as will be shown in Exercise 3.2Z.
- The binary probability mass functions $P_U(U)$ and $P_V(V)$ are obtained according to the modulo operations $U = X \hspace{0.1cm}\text{mod} \hspace{0.1cm}2$ and $V = Y \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2$.
Questions
Solution
(1) In general, the following applies to the expected value of the function $F(X)$ with respect to the random variable $X$:
- $${\rm E} \left [ F(X)\right ] = \hspace{-0.4cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} {\rm supp} (P_X)} \hspace{-0.2cm} P_{X}(x) \cdot F(x) \hspace{0.05cm}.$$
In the present example, $X = \{0,\ 1,\ 2,\ 3\}$ and $P_X(X) = \big [1/2, \ 1/8, \ 0, \ 3/8\big ]$.
- Because of $P_X(X = 2) = 0$ , the quantity to be taken into account (the "support") in the above summation thus results in
- $${\rm supp} (P_X) = \{ 0\hspace{0.05cm}, 1\hspace{0.05cm}, 3 \} \hspace{0.05cm}.$$
- With $F(X) = 1/P_X(X)$ one further obtains:
- $${\rm E} \big [ 1/P_X(X)\big ] = \hspace{-0.4cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{-0.4cm} P_{X}(x) \cdot {1}/{P_X(x)} = \hspace{-0.4cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{-0.3cm} 1 \hspace{0.15cm}\underline{ = 3} \hspace{0.05cm}.$$
- The second expected value gives the same result with ${\rm supp} (P_Y) = \{ 0\hspace{0.05cm}, 1\hspace{0.05cm}, 2 \} $ :
- $${\rm E} \left [ 1/P_Y(Y)\right ] \hspace{0.15cm}\underline{ = 3}.$$
(2) In both cases, the index of the probability mass function is identical with the random variable $(X$ or $Y)$ and we obtain
- $${\rm E} \big [ P_X(X)\big ] = \hspace{-0.3cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{-0.3cm} P_{X}(x) \cdot {P_X(x)} = (1/2)^2 + (1/8)^2 + (3/8)^2 = 13/32 \hspace{0.15cm}\underline{ \approx 0.406} \hspace{0.05cm},$$
- $${\rm E} \big [ P_Y(Y)\big ] = \hspace{-0.3cm} \sum_{y \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 2 \}} \hspace{-0.3cm} P_Y(y) \cdot P_Y(y) = (1/2)^2 + (1/4)^2 + (1/4)^2 \hspace{0.15cm}\underline{ = 0.375} \hspace{0.05cm}.$$
(3) The following equations apply here:
- $${\rm E} \big [ P_Y(X)\big ] = \hspace{-0.3cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{-0.3cm} P_{X}(x) \cdot {P_Y(x)} = \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{8} \cdot \frac{1}{4} + \frac{3}{8} \cdot 0 = 9/32 \hspace{0.15cm}\underline{ \approx 0.281} \hspace{0.05cm},$$
- The expected value formation here refers to $P_X(·)$, i.e. to the random variable $X$.
- $P_Y(·)$ is the formal function without (direct) reference to the random variable $Y$.
- The same numerical value is obtained for the second expected value (this does not have to be the case in general):
- $${\rm E} \big [ P_X(Y)\big ] = \hspace{-0.3cm} \sum_{y \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 2 \}} \hspace{-0.3cm} P_{Y}(y) \cdot {P_X(y)} = \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{8} + \frac{1}{4} \cdot 0 = 9/32 \hspace{0.15cm}\underline{ \approx 0.281} \hspace{0.05cm}.$$
(4) We first calculate the three expected values:
- $${\rm E} \big [-{\rm log}_2 \hspace{0.1cm} P_U(U)\big ] = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{1} + \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{1} \hspace{0.15cm}\underline{ = 1\ {\rm bit}} \hspace{0.05cm},$$
- $${\rm E} \big [-{\rm log}_2 \hspace{0.1cm} P_V(V)\big ] = \frac{3}{4} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{3} + \frac{1}{4} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{1} \hspace{0.15cm}\underline{ = 0.811\ {\rm bit}} \hspace{0.05cm},$$
- $${\rm E} \big [-{\rm log}_2 \hspace{0.1cm} P_V(U)\big ] = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{3} + \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{1} \hspace{0.15cm}\underline{ = 1.208\ {\rm bit}} \hspace{0.05cm}.$$
Accordingly, the first two statements are correct:
- The entropy $H(U) = 1$ bit can be calculated according to the first equation. It applies to the binary random variable $U$ with equal probabilities.
- The entropy $H(V) = 0.811$ bit is calculated according to the second equation. Due to the probabilities $3/4$ and $1/4$ , the entropy (uncertainty) is smaller here than for the random variable $U$.
- The third expected value cannot indicate the entropy of a binary random variable, which is always limited to $1$ (bit) , simply because of the result $(1.208$ bit$)$ .