Exercise 3.2: Laplace Transform

Three causal time functions

Causal signals and systems are usually described by means of the Laplace transformation. If $x(t)$ is identical to zero for all times $t < 0$, then the Laplace transform is:

$$X_{\rm L}(p) = \int_{0}^{ \infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}\hspace{0.05cm} .$$

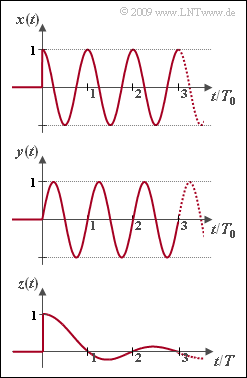
In this exercise, the Laplace transforms of the causal signals shown in the graph are to be determined. The following equations are valid in each case only for $t \ge 0$. For negative times, all signals are identical to zero.

Cosine signal with period $T_0$:

$$x(t) = {\rm cos} (2\pi \cdot {t}/{T_0})= {\rm cos} (\omega_0 \cdot t) \hspace{0.05cm},$$

sine signal with period $T_0$:

$$y(t) = {\rm sin} (2\pi \cdot {t}/{T_0})= {\rm sin} (\omega_0 \cdot t) \hspace{0.05cm},$$

$\sin(t)/t$–signal with equivalent zero-crossings at a distance of $T$:

$$z(t) = {\rm si} (\pi \cdot {t}/{T})= {\rm sinc} ({t}/{T})\hspace{0.4cm}{\rm with}\hspace{0.4cm}{\rm si}(x)= {\rm sin}(x)/x ={\rm sinc}(x)/\pi \hspace{0.05cm}.$$

The following equation cannot be used to calculate the spectral function since $z(t)$ is not energy-limited just as the signals $x(t)$ and $y(t)$ :

$$Z(f) = Z_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it f}} .$$

Rather, the fact that $z(t) = s(t) \cdot \gamma(t)$ holds is to be considered where $s(t)$ denotes the conventional symmetric $\rm si$–function here:

$$s(t) = {\rm si} (\pi \cdot {t}/{T}) \quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad S(f).$$

$S(f)$ is a rectangular function symmetric about $f = 0$ with height $T$ and width $1/T$.

The Fourier transform of the step function $\gamma(t)$ is:

$$\gamma(t) \quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad {\it \Gamma}(f) = {1}/{2} \cdot \delta (f) + \frac{1}{{\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$

Please note:

The exercise belongs to the chapter Laplace Transform and p-Transfer Function.
In the sample solution, we use of the two comparable functions ${\rm si}(x)$ and ${\rm sinc}(x)$ the former.
The following definite integrals are given:

$$\int_{0}^{ \infty} { {\rm e}^{-p x} \cdot \cos(qx)}\hspace{0.1cm}{\rm d}x = \frac{p}{p^2 + q^2}\hspace{0.05cm} , \hspace{1.0cm}\int_{0}^{ \infty} { {\rm e}^{-p x} \cdot \sin(qx)}\hspace{0.1cm}{\rm d}x = \frac{q}{p^2 + q^2}\hspace{0.05cm} , $$

$$\int_{0}^{ \infty} { {\rm e}^{-p x} \cdot \frac{\sin(qx)}{x}}\hspace{0.1cm}{\rm d}x = {\rm arctan}\hspace{0.15cm}\frac{q}{p}\hspace{0.05cm} , \hspace{0.6cm} \int_{A}^{ B} { \frac{1}{x}}\hspace{0.1cm}{\rm d}x = {\rm ln}\hspace{0.15cm}\frac{B}{A}\hspace{0.05cm} .$$

Questions

Solution

(1) Suggested solution 2 is correct:

According to the Laplace definition, the following holds with the given equations:

$$X_{\rm L}(p) = \int_{0}^{ \infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t = \int\limits_{0}^{ \infty} { {\rm cos} (\omega_0 \cdot T) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t = \frac{p}{p^2 + \omega_0^2} \hspace{0.05cm} .$$

Suggestion 3 is ruled out since $X_{\rm L}(p)$ must have the unit "second" (integral over time) while $p$ and $\omega_0$ each have the unit "1/s".

(2) Suggested solution 1 is correct:

Here, the following holds using the same approach as in the subtask (1):

$$Y_{\rm L}(p) = \int_{0}^{ \infty} { {\rm sin} (\omega_0 \cdot T) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t = \frac{\omega_0}{p^2 + \omega_0^2} \hspace{0.05cm} .$$

(3) Suggested solution 3 is correct:

The $p$–transfer function of the causal $\rm si$–function is as follows considering the integral given above:

$$Z_{\rm L}(p) = \int_{0}^{ \infty} { \frac{\sin(\pi \cdot t/T)}{\pi \cdot t/T} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t = \frac{T}{\pi} \cdot {\rm arctan} \; \frac{\pi}{p\cdot T} \hspace{0.05cm} .$$

Suggestion 1 only applies to the Fourier transform of the non-causal $\rm si$–function.
Since here the argument of the $\rm arctan$ function is dimensional, suggestion 2 cannot be true for this reason alone.

(4) Suggested solution 1 is correct:

The following arises as a result from $z(t) = s(t) \cdot \gamma(t)$ with the convolution theorem:

$$Z(f) = S(f) \star {\it \Gamma}(f) = {1}/{2} \cdot S(f) \star \delta (f) + S(f) \star \frac{1}{{\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$

Since $S(f)$ is real, the real part of $Z(f)$ is obtained as the first term of this equation:

$${\rm Re}[ Z(f)] = {1}/{2} \cdot S(f) \star \delta (f) = {1}/{2} \cdot S(f) \hspace{0.05cm}.$$

The real part of $Z(f)$ thus has the same rectangular shape as $S(f)$, but it is only half as high:

$${\rm Re}\{ Z(f)\}= \left\{ \begin{array}{c} T/2 \\ 0 \end{array} \right. \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array} \begin{array}{*{20}c} { |f|< 1/(2T)\hspace{0.05cm},} \\ { |f|> 1/(2T)\hspace{0.05cm},} \end{array} \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{{\rm suggestion \hspace{0.15cm} 1}}.$$

(5) Suggested solution 2 is correct:

With the result of the last subtask, it follows for the imaginary part:

$${\rm Im}\{ Z(f)\} = S(f) \star \frac{(-1)}{{\rm j} \cdot 2\pi f} \hspace{0.05cm}.$$

This convolution integral yields the following for sufficiently large frequencies $f \ge 1/(2T)$:

$${\rm Im}\{ Z(f)\} = -T \cdot \int_{f- 1/(2T)}^{ f+ 1/(2T)} { \frac{1}{2\pi x}}\hspace{0.1cm}{\rm d}x = \frac{T}{2\pi } \cdot {\rm ln}\hspace{0.15cm}\left |\frac{f- 1/(2T)}{f+ 1/(2T)}\right | \hspace{0.05cm} \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{{\rm suggestion \hspace{0.15cm} 2}}.$$

	$X_{\rm L}(p) = \omega_0/(p^2 + \omega_0^2)$.
	$X_{\rm L}(p) = p/(p^2 + \omega_0^2)$.
	$X_{\rm L}(p) = 1/(p^2 + \omega_0^2)$.

	$Y_{\rm L}(p) = \omega_0/(p^2 + \omega_0^2)$.
	$Y_{\rm L}(p) = p/(p^2 + \omega_0^2)$.
	$Y_{\rm L}(p) = 1/(p^2 + \omega_0^2)$.

	$Z_{\rm L}(p)$ has a rectangular shape.
	$Z_{\rm L}(p) = \arctan (1/p)$.
	$Z_{\rm L}(p) = T/\pi \cdot \arctan (\pi/(pT))$.

	${\rm Re}\big[Z(f)\big]$ has a rectangular shape.
	${\rm Re}\big[Z(f)\big]$ is proportional to $\ln\; \big\|(f \cdot T -0.5)/(f \cdot T +0.5)\big\|.$

	${\rm Im}\big[Z(f)\big]$ has a rectangular shape.
	${\rm Im}\big[Z(f)\big]$ is proportional to $\ln\; \big\|(f \cdot T -0.5)/(f \cdot T +0.5)\big\|.$