Exercise 3.4: Entropy for Different PMF
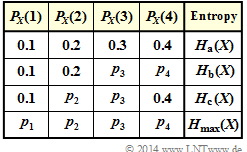
In the first row of the adjacent table, the probability mass function denoted by $\rm (a)$ is given in the following.
For this PMF $P_X(X) = \big [0.1, \ 0.2, \ 0.3, \ 0.4 \big ]$ the entropy is to be calculated in subtask (1) :
- $$H_{\rm a}(X) = {\rm E} \big [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\big ]= - {\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_{X}(X)}\big ].$$
Since the logarithm to the base $2$ is used here, the pseudo-unit "bit" is to be added.
In the further tasks, some probabilities are to be varied in each case in such a way that the greatest possible entropy results:
- By suitably varying $p_3$ and $p_4$, one arrives at the maximum entropy $H_{\rm b}(X)$ under the condition $p_1 = 0.1$ and $p_2 = 0.2$ ⇒ subtask (2).
- By varying $p_2$ and $p_3$ appropriately, one arrives at the maximum entropy $H_{\rm c}(X)$ under the condition $p_1 = 0.1$ and $p_4 = 0.4$ ⇒ subtask (3).
- In subtask (4) all four parameters are released for variation, which are to be determined according to the maximum entropy ⇒ $H_{\rm max}(X)$ .
Hints:
- The exercise belongs to the chapter Some preliminary remarks on two-dimensional random variables.
- In particular, reference is made to the page Probability mass function and entropy.
Questions
Solution
- $$H_{\rm a}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} + 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.15cm} \underline {= 1.846} \hspace{0.05cm}.$$
Here (and in the other tasks) the pseudo-unit "bit" is to be added in each case.
(2) The entropy $H_{\rm b}(X)$ can be represented as the sum of two parts $H_{\rm b1}(X)$ and $H_{\rm b2}(X)$, with:
- $$H_{\rm b1}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} = 0.797 \hspace{0.05cm},$$
- $$H_{\rm b2}(X) = p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} + (0.7-p_3) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.7-p_3} \hspace{0.05cm}.$$
- The second function is maximum for $p_3 = p_4 = 0.35$. A similar relationship has been found for the binary entropy function.
- Thus one obtains:
- $$H_{\rm b2}(X) = 2 \cdot p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} = 0.7 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.35} = 1.060 $$
- $$ \Rightarrow \hspace{0.3cm} H_{\rm b}(X) = H_{\rm b1}(X) + H_{\rm b2}(X) = 0.797 + 1.060 \hspace{0.15cm} \underline {= 1.857} \hspace{0.05cm}.$$
(3) Analogous to subtask (2), $p_1 = 0.1$ and $p_4 = 0.4$ yield the maximum for $p_2 = p_3 = 0.25$:
- $$H_{\rm c}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 2 \cdot 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} + 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.15cm} \underline {= 1.861} \hspace{0.05cm}.$$
(4) The maximum entropy for the symbol range $M=4$ is obtained for equal probabilities, i.e. for $p_1 = p_2 = p_3 = p_4 = 0.25$:
- $$H_{\rm max}(X) = {\rm log}_2 \hspace{0.1cm} M \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}.$$
- The difference of the entropies according to (4) and (3) gives ${\rm \Delta} H(X) = 0.139 \ \rm bit$. Here:
- $${\rm \Delta} H(X) = 1- 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} - 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.05cm}.$$
- With the binary entropy function
- $$H_{\rm bin}(p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}$$
- can also be written for this:
- $${\rm \Delta} H(X) = 0.5 \cdot \big [ 1- H_{\rm bin}(0.2) \big ] = 0.5 \cdot \big [ 1- 0.722 \big ] = 0.139 \hspace{0.05cm}.$$