Exercise 3.6: Adaptive Multi Rate Codec

• Return to book

Tracks of the AMR codec

In the late 1990s,  a very flexible,  adaptive speech codec was developed and standardized in the form of  $\rm AMR$  codec.  This provides a total of eight different modes with data rates between  $4.75 \ \rm kbit/s$  and  $12.2 \ \rm kbit/s$.

The AMR codec,  like the full rate codec  $\rm (FRC)$  discussed in  $\text{Exercise 3.5}$,  includes both a short-term prediction  $\rm (LPC)$  and a long-term prediction  $\rm (LTP)$.  However,  these two components are realized differently from FRC.

The main difference between AMR and FRC is the encoding of the residual signal  $($after LPC and LTP$)$:

1. Instead of  "Regular Pulse Excitation"  $\rm (RPE)$,  here the  "Algebraic Code Excitation Linear Prediction"  $\rm (ACELP)$  is used.
2. From the fixed code book  $\rm (FCB)$,  for each subframe of  $5 \ \rm ms$  duration,  the  "FCB pulse"  and the  "FCB gain"  that best match the residual signal  $($for which the mean square error of the difference signal becomes minimum$)$  is selected.

Each entry in the fixed code book identifies a pulse where exactly  $10$  of  $40$  positions are occupied by  $\pm1$. 

In this regard it should be noted:

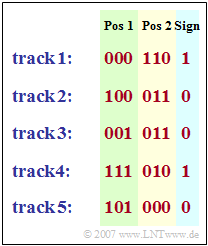
• The pulse is divided into five tracks with eight possible positions each, where track  $1$  contains the positions  $1,\ 6,\ 11$, ... , $36$  of the subframe and track  $5$  describes the positions  $5,\ 10,\ 15$, ... , $40$.

• In each track there are exactly two values  $\pm1$,  while all the other six values are  zero. 

• The two  $±1$-positions are each assigned three bits –   i.e. encoded with  "$000$", ... ,  "$111$".

• Another bit is used for the  "sign of the first-mentioned pulse",  where a  "$1$"  indicates a positive sign and a  "$0$"  a negative sign.

• If the pulse position of the second pulse is greater than that of the first pulse,  the second pulse has the same sign as the first,  otherwise the opposite.

• Thus,  seven bits per track are transmitted to the receiver,  plus five bits for the so-called  "FCB amplification.

In the diagram,  the  $35$  bits describing an FCB pulse are given as an example:

⇒   Track 1  includes

1. a positive pulse  $({\rm sign} = 1)$  at position  $\big [1$  (first possible position for track 1)  $\hspace{0.02cm}\text{plus}\hspace{0.2cm}0$  (bit specification for  "000") $= 1\big]$,
2. another positive pulse  $($since $110 > 000)$  at position  $\big [1 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5$ (pulse spacing in each track) $\hspace{0.02cm}\text{times}\hspace{0.2cm}6$  (bit specification for " 110") = $31\hspace{0.05cm}\big].$

Track 2 includes.

1. a negative pulse (${\rm sign} = 0$)  at position  $\big [2$ (first possible position for track 2)  $\hspace{0.02cm}\text{plus}\hspace{0.2cm}5\hspace{0.2cm}\text{times}\hspace{0.2cm}4$  (bit specification for  " 100")  $=22\hspace{0.05cm}\big],$
2. a positive pulse  $($sign reversal due to  $011 > 100)$  at position  $\big [2 \hspace{0.2cm}\text{plus}\hspace{0.2cm}5\hspace{0.2cm}\text{times}\hspace{0.2cm}3$  (bit specification for  " 011")  $=17\hspace{0.05cm}\big].$

Hint:

• This exercise belongs to the chapter  "Speech Coding".

• When entering the pulse positions  $N_{1}$  denotes the first triple of bits and  $N_{2}$  the second.

• For example,  for track  $2$  one would have to enter the values  $N_{1}=-22$  and  $N_{2}=+17$.

Questions

1

How many bits describe a speech frame $($of duration  $20 \ \rm ms)$  in  $12.2 \ \rm kbit/s$ mode?

$N_{12.2} \ = \ $ $ \ \rm bits$

2

How many bits are needed for FCB pulse and gain per frame?

$N_{\rm FCB} \ = \ $ $ \ \rm bits$

3

How many bits are left for LPC and LTP?

$N_{\rm LPC/LTP} \ = \ $ $ \ \rm bits$

4

What subframe pulse positions and signs does track  $3$  describe?  Follow the instructions for input on the information page.

$N_{1} \ = \ $

$N_{2} \ = \ $

5

What pulse positions including sign describe the track  $4$?

$N_{1} \ = \ $

$N_{2} \ = \ $

6

What pulse positions including sign describe the track  $5$?

$N_{1} \ = \ $

$N_{2} \ = \ $

Solution

Solution

(1)  With the data rate  $R_{\rm C} = 12.2 \ \rm kbit/s$,  exactly  $\underline{244 \ \rm bits}$  results within  $20 \ \rm ms$,  while e.g. in  $4.75 \ \rm kbit/s$  mode only  $95 \ \rm bits$  are transmitted.

(2)  In each subframe,  the FCB pulse requires  $35 \ \rm bits$  (five tracks of seven bits each)  and the FCB gain requires five bits.

• With four subframes,  this gives $N_{\rm FCB} \hspace{0.15cm}\underline{= 160 \ \rm bits}$.

(3)  This leaves the difference from  (1)  and  (2),  i.e. $N_{\rm LPC/LTP}\hspace{0.15cm} \underline{ = 84\ \rm bits}$.

(4)  The sign bit  "$0$"  indicates a negative first pulse.

• Because  $001 < 011$,  the second pulse has the same sign.

• The two magnitudes result in

$$|N_1| \ = \ 3 \hspace{0.1cm}{\rm(since \hspace{0.1cm} track \hspace{0.1cm}3)} + 5\cdot 1 \hspace{0.1cm} {\rm(bit\:specification \hspace{0.1cm} 001)} = 8\hspace{0.05cm}, $$

$$ |N_2| \ = \ 3 \hspace{0.1cm}{\rm(since \hspace{0.1cm} track \hspace{0.1cm}3)} + 5\cdot 3 \hspace{0.1cm} {\rm(bit\:specification \hspace{0.1cm} 011)} = 18\hspace{0.05cm}.$$

• Therefore,  to be entered for the third track is  $N_{1}\hspace{0.15cm} \underline{ = -8}$  and  $N_{2} \hspace{0.15cm}\underline{ = -18}.$

(5)  In an analogous way,  for track  $4$  we obtain the values  $N_{1}\hspace{0.15cm} \underline{ = +39}$  and  $N_{2}\hspace{0.15cm} \underline{ = -14}$.

(6)  The fifth track provides  $N_{1}\hspace{0.15cm} \underline{ =-30}$  and  $N_{2}\hspace{0.15cm} \underline{ = +5}$