Exercise 3.7Z: Partial Fraction Decomposition

Pole-zero diagrams

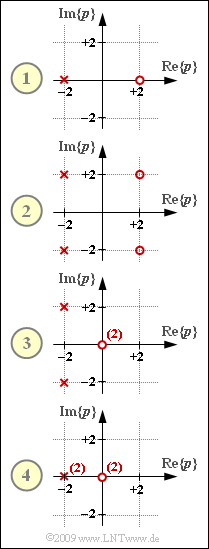
In the graph, four two-port networks are given by their pole–zero diagrams $H_{\rm L}(p)$.

They all have in common that the number $Z$ of zeros is equal to the number $N$ of poles.
The constant factor in each case is $K=1$.

In the special case $Z = N$ the residue theorem cannot be applied directly to compute the impulse response $h(t)$.

Rather, a "partial fraction decomposition" corresponding to

$$H_{\rm L}(p) =1- H_{\rm L}\hspace{0.05cm}'(p) \hspace{0.05cm}$$

must be made beforehand. Then,

$$h(t) = \delta(t)- h\hspace{0.03cm}'(t) \hspace{0.05cm}$$

holds for the impulse response. $h\hspace{0.03cm}'(t)$ is the inverse Laplace transform of $H_{\rm L}\hspace{0.05cm}'(p)$, where the condition $Z' < N'$ is satisfied.

Two of the four configurations given are so-called "all-pass filters".

This refers to two-port networks for which the Fourier spectrum satisfies the condition $|H(f)| = 1$ ⇒ $a(f) = 0$ .
In Exercise 3.4Z it is given how the poles and zeros of such an all-pass filter must be positioned.

Furthermore, in this exercise the $p$–transfer function

$$H_{\rm L}^{(5)}(p) =\frac{p/A}{\left (\sqrt{p/A}+\sqrt{A/p} \right )^2} \hspace{0.05cm}$$

⇒ "configuration $(5)$" will be examined in more detail, which can be represented by one of the four pole–zero diagrams given in the graph if the parameter $A$ is chosen correctly.

Please note:

The exercise belongs to the chapter Inverse Laplace Transform.
In particular, reference is made to the page Partial fraction decomposition.

Questions

Solution

(1) The suggested solutions 1 and 2 are correct:

According to the criteria given in exercise 3.4Z, there is always an all-pass filter at hand
if there is a corresponding zero $p_{\rm o} = + A + {\rm j} \cdot B$ in the right $p$–half-plane for each pole $p_{\rm x} = - A + {\rm j} \cdot B$ in the left half-plane.
Considering $K = 1$ the attenuation function is then $a(f) = 0 \ \rm Np$ ⇒ $|H(f)| = 1$.
The following can be seen from the graph on the information page: The configurations $(1)$ and $(2)$ satisfy exactly these symmetry properties.

(2) The suggested solution 4 is correct:

The transfer function $H_{\rm L}^{(5)}(p)$ is also described by configuration $(4)$ as the following calculation shows:

$$H_{\rm L}^{(5)}(p) \hspace{0.25cm} = \hspace{0.2cm} \frac{p/A}{(\sqrt{p/A}+\sqrt{A/p})^2} =\frac{p/A}{{p/A}+2+ {A/p}} = \hspace{0.2cm}\frac{p^2}{p^2 + 2A \cdot p + A^2} = \frac{p^2}{(p+A)^2 }= H_{\rm L}^{(4)}(p) \hspace{0.05cm}.$$

The double zero is at $p_{\rm o} = 0$ and the double pole at $p_{\rm x} = -A = -2$.

(3) The following holds for configuration $(1)$:

$$H_{\rm L}(p) =\frac{p-2}{p+2}=\frac{p+2-4}{p+2}= 1 - \frac{4}{p+2}=1- H_{\rm L}\hspace{-0.05cm}'(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{-0.05cm}'(p) = \frac{4}{p+2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\hspace{0.15cm}\underline{H_{\rm L}\hspace{-0.05cm}'(p =0) =2} \hspace{0.05cm}.$$

(4) Similarly, the following is obtained for configuration $(2)$:

$$H_{\rm L}(p) =\frac{(p-2 - {\rm j} \cdot 2)(p-2 + {\rm j} \cdot 2)}{(p+2 - {\rm j} \cdot 2)(p+2 + {\rm j} \cdot 2)}= \frac{p^2 -4\cdot p +8 }{p^2 +4\cdot p +8}= \hspace{0.2cm}\frac{p^2 +4\cdot p +8 -8\cdot p}{p^2 +4\cdot p +8} =1- \frac{8\cdot p}{p^2 +4\cdot p +8}=1- H_{\rm L}\hspace{-0.05cm}'(p)$$

$$\Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{0.05cm}'(p) = 8 \cdot \frac{p}{(p+2 - {\rm j} \cdot 2)(p+2 + {\rm j} \cdot 2)} \hspace{0.05cm}.$$

Thus, the suggested solutions 2 and 3 are correct in contrast to statement 1:

While $H_{\rm L}(p)$ has two conjugate complex zeros,
$H_{\rm L}\hspace{0.01cm}'(p)$ only has a single zero at $p_{\rm o}\hspace{0.01cm}' = 0$.

(5) The following applies for configuration $(3)$ :

$$H_{\rm L}(p) = \frac{p^2 }{p^2 +4\cdot p +8}=\frac{p^2 +4\cdot p +8 -4\cdot p -8 }{p^2 +4\cdot p +8} = 1- H_{\rm L}\hspace{-0.05cm}'(p)$$

$$\Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{-0.05cm}'(p) = 4 \cdot \frac{p+2}{(p+2 - {\rm j} \cdot 2)(p+2 + {\rm j} \cdot 2)} \hspace{0.05cm}.$$

The zero of $H_{\rm L}\hspace{0.01cm}'(p)$ is now at $p_{\rm o}\hspace{0.01cm}' = -2$.
The constant is $K\hspace{0.01cm}' = 4$ ⇒ only suggested solution 2 is correct here.

(6) Finally, the following holds for configuration $(4)$:

$$H_{\rm L}(p) = \frac{p^2 }{(p+2)^2}=\frac{p^2 +4\cdot p +4 -4\cdot p -4 }{p^2 +4\cdot p +4} = 1- \frac{4\cdot p +4 }{p^2 +4\cdot p +4} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{0.05cm}'(p) = 4 \cdot \frac{p+1}{(p+2)^2} \hspace{0.05cm}.$$

Suggested solution 2 is correct here. In general, it can be said that:

The partial fraction decomposition changes the number and position of the zeros.
On the contrary, the poles of $H_{\rm L}\hspace{0.01cm}'(p)$ are always identical to those of $H_{\rm L}(p)$.

	Configuration $(1)$,
	configuration $(2)$,
	configuration $(3)$,
	configuration $(4)$.

	Configuration $(1)$,
	configuration $(2)$,
	configuration $(3)$,
	configuration $(4)$.

	$H_{\rm L}\hspace{0.01cm}'(p)$ has the same zeros as $H_{\rm L}(p)$.
	$H_{\rm L}\hspace{0.01cm}'(p)$ has the same poles as $H_{\rm L}(p)$.
	The constant factor of $H_{\rm L}\hspace{0.01cm}'(p)$ is $K' = 8$.