Exercise 4.07: Decision Boundaries once again
We consider a transmission system with
- only one basis function $(N = 1)$,
- two signals $(M = 2)$ with $s_0 = \sqrt{E_s}$ and $s_1 = -\sqrt{E_s}$ ,
- an AWGN channel with variance $\sigma_n^2 = N_0/2$.
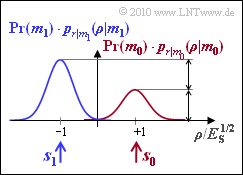
Since this exercise deals with the general case ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$, it is not sufficient to consider the conditional density functions $p_{\it r\hspace{0.05cm}|\hspace{0.05cm}m_i}(\rho\hspace{0.05cm} |\hspace{0.05cm}m_i)$. Rather, these must still be multiplied by the symbol probabilities ${\rm Pr}(m_i)$. For $i$, the values $0$ and $1$ have to be used here.
If the decision boundary between the two regions $I_0$ and $I_1$ is at $G = 0$, i.e., in the middle between $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$, the error probability is independent of the occurrence probabilities ${\rm Pr}(m_0)$ and ${\rm Pr}(m_1)$:
- $$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) \hspace{0.05cm}.$$
- Here $d$ indicates the distance between the signal points $s_0$ and $s_1$ and $d/2$ accordingly the respective distance of $s_0$ and $s_1$ from the decision boundary $G = 0$.
- The rms value (root of the variance) of the AWGN noise is $\sigma_n$.
If, on the other hand, the occurrence probabilities are different ⇒ ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$, a smaller error probability can be obtained by shifting the decision boundary $G$:
- $$p_{\rm S} = {\rm Pr}(m_1) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 + \gamma) \right ) + {\rm Pr}(m_0) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 - \gamma) \right )\hspace{0.05cm},$$
where the auxiliary quantity $\gamma$ is defined as follows:
- $$\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} \hspace{0.05cm},\hspace{0.2cm} G_{\rm opt} = \gamma \cdot \sqrt {E_{\rm S}}\hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Approximation of the Error Probability".
- You can find the values of the Q–function with interactive applet "Complementary Gaussian Error Functions".
Questions
Solution
- $${\rm Pr}(m_1) = 2 \cdot {\rm Pr}(m_0) \hspace{0.05cm},\hspace{0.2cm} {\rm Pr}(m_0) + {\rm Pr}(m_1) = 1$$
- it follows directly ${\rm Pr}(m_0) = 1/3 \ \underline {\approx 0.333}$ and ${\rm Pr}(m_1) = 2/3 \ \underline {\approx 0.667}$.
(2) With the decision boundary $G = 0$, independently of the occurrence probabilities:
- $$p_{\rm S} = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) \hspace{0.05cm}.$$
- With $d = 2 \cdot \sqrt{E_{\rm S}}$ and $\sigma_n = \sqrt{E_{\rm S}}/3$, this gives:
- $$p_{\rm S} = {\rm Q} (3) \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.135 \%} \hspace{0.05cm}.$$
(3) According to the specification, for the "normalized threshold":
- $$\gamma = \frac{G_{\rm opt}}{E_{\rm S}^{1/2}} = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} = \frac{ 2 \cdot E_{\rm S}/9}{4 \cdot E_{\rm S}} \cdot {\rm ln} \hspace{0.15cm} \frac{2/3}{1/3} \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.04} \hspace{0.05cm}.$$
- Thus, $G_{\rm opt} = \gamma \cdot \sqrt{E_{\rm S}} = 0.04 \cdot \sqrt{E_{\rm S}}$.
- Thus, the optimal decision boundary is shifted to the right $($towards the more improbable symbol $s_0)$, because ${\rm Pr}(m_0) < {\rm Pr}(m_1)$.
(4) With this optimal decision boundary, the error probability is slightly smaller compared to subtask (2):
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {2}/{3} \cdot {\rm Q} (3 \cdot 1.04) + {1}/{3} \cdot {\rm Q} (3 \cdot 0.96) = {2}/{3} \cdot 0.090 \cdot 10^{-2} + {1}/{3} \cdot 0.199 \cdot 10^{-2} \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.126 \%} \hspace{0.05cm}.$$
(5) With the decision boundary in the middle between the symbols $(G = 0)$, the result is analogous to subtask (2) with the noise variance now larger:
- $$p_{\rm S} = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) = {\rm Q} \left ( \frac{\sqrt{E_{\rm S}}}{\sqrt{E_{\rm S}}} \right )= {\rm Q} (1)\hspace{0.1cm} \hspace{0.15cm}\underline {\approx 15.9 \%} \hspace{0.05cm}.$$
- The parameter $\gamma$ (normalized best possible displacement of the decision boundary) is
- $$\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} = \frac{ 2 \cdot E_{\rm S}}{4 \cdot E_{\rm S}} \cdot {\rm ln} \hspace{0.15cm} \frac{2/3}{1/3} = \frac{{\rm ln} \hspace{0.15cm} 2}{2} \approx 0.35 $$
- $$\Rightarrow \hspace{0.3cm} G_{\rm opt} = 0.35 \cdot \sqrt{E_{\rm S}} \hspace{0.05cm}.$$
- The more frequent symbol is now less frequently falsified ⇒ the mean error probability becomes smaller:
- $$p_{\rm S} = {2}/{3} \cdot {\rm Q} (1.35) + {1}/{3} \cdot {\rm Q} (0.65) = {2}/{3} \cdot 0.0885 +{1}/{3} \cdot 0.258 \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 14.5 \%} \hspace{0.05cm}.$$
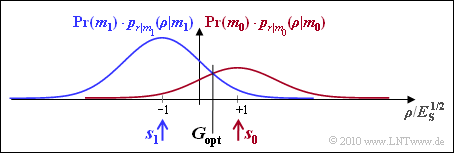
- The sketch makes it clear that the optimal decision boundary can also be determined graphically as intersection of the two (weighted) probability density functions:
(6) All solutions of this rather academic subtask are correct:
- With threshold $G = 0$, we get $p_{\rm S} = {\rm Q}(0.5) \ \underline {\approx 0.309}$.
- The parameter $\gamma = 1.4$ now has four times the value compared to subtask (5),
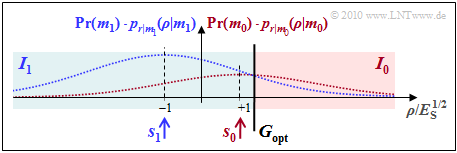
so that the optimal decision boundary is now $G_{\rm opt} = \underline {1.4 \cdot s_0}$. - Thus, the (noiseless) signal value $s_0$ does not belong to the decision region $I_0$, but to $I_1$, characterized by $\rho < G_{\rm opt}$.
- Only with a (positive) noise component: $I_0 (\rho > G_{\rm opt})$ is possible at all. For the error probability, with $G_{\rm opt} = 1.4 \cdot s_0$:
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {2}/{3} \cdot {\rm Q} (0.5 \cdot (1 + 1.4)) + {1}/{3} \cdot {\rm Q} (0.5 \cdot (1 - 1.4)) = \hspace{0.15cm}\underline {\approx 27\%} \hspace{0.05cm}.$$
- The accompanying graph illustrates the statements made here.