Exercise 4.12: Calculations for the 16-QAM
From LNTwww
Signal space constellation of $\rm 16–QAM$
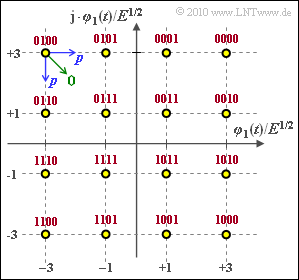
The graph shows the signal space constellation of "quadrature amplitude modulation" with $M = 16$ signal space points. The following should be calculated for this modulation method:
- the average energy per symbol or per bit,
- the average symbol error probability $p_{\rm S}$,
- the "Union Bound" $p_{\rm UB}$ as upper bound,
- the average bit error probability $p_{\rm B}$ with Gray coding.
Notes:
- The exercise deals with a partial aspect of the chapter "Carrier Frequency Systems with Coherent Demodulation".
- The Gray assignment is given in the graphic $($red lettering$)$.
- The probability that the upper left symbol is falsified into one of the neighboring symbols is abbreviated to $p$ $($blue arrows in the graph$)$.
- A diagonal falsification ⇒ two bit falsified $($green arrow$)$ is excluded.
- For the AWGN channel, with the complementary Gaussian error integral for this auxiliary variable, the following applies: $p = {\rm Q} \left ( \sqrt{ { 2E}/{ N_0} }\right )\hspace{0.05cm}.$
- For numerical calculations, use $E = 1 \ \rm mWs$ and $p = 0.4\%$.
- The AWGN noise power density $N_0$ can be calculated approximately from these values:
- $$p = {\rm Q} \left ( \sqrt{ { 2E}/{ N_0} }\right ) = 0.004 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} { 2E}{ N_0} \approx 2.65^2 \approx 7 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} N_0 = { E}/{ 3.5}\approx 1.4 \cdot 10^{-4}\,{\rm W/Hz} \hspace{0.05cm}.$$
Questions
Solution
(1) The quotient $E_{\rm S}/E$ is obtained as the mean square distance of the $M = 16$ signal space points $\boldsymbol{s}_i$ from the origin.
- With the given signal space constellation of the $\rm 16–QAM$ we obtain:
- $$E_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} { E}/{ 16} \cdot \left [ 4 \cdot (1^2 + 1^2) + 8 \cdot (1^2 + 3^2) + 4 \cdot (3^2 + 3^2)\right ]={ E}/{ 16} \cdot \left [ 4 \cdot 2 + 8 \cdot 10 + 4 \cdot 18\right ] = 10 \cdot E = \underline{10 \ {\rm mWs}} \hspace{0.05cm}.$$
- The same result is obtained with the equation given in the "theory section":
- $$E_{\rm S} = \frac{ 2 \cdot (M-1)}{ 3 } \cdot E = \frac{ 2 \cdot 15}{ 3 } \cdot E = 10 E \hspace{0.05cm}.$$
(2) Each individual symbol represents four binary symbols. Thus, the average energy per bit is
- $$E_{\rm B} = \frac{ E_{\rm S}}{ {\rm log_2} \hspace{0.05cm}(M)} = 2.5 \cdot E = \underline{2.5 \ {\rm mWs}} \hspace{0.05cm}.$$
Illustration: 16–QAM error probability
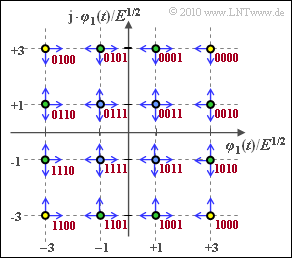
(3) The "Union Bound" is an upper bound on the symbol error probability.
- It only takes into account the transition to adjacent decision regions due to AWGN noise.
- From the graph, it can be seen that the corner symbols (filled in yellow) can only be biased towards two other symbols and the remaining edge symbols (filled in green) can be biased in three directions.
- The "worst case" are the four inner symbols (with blue filling) with four falsification possibilities each.
- From this follows:
- $$p_{\rm S} = {\rm Pr}({\cal{E}}) \le 4 \cdot p = \underline{1.6\%}= p_{\rm UB} \hspace{0.05cm}.$$
(4) Counting the blue arrows in the above graph, we get
- $$4 \cdot 2 + 8 \cdot 3 + 4 \cdot 4 = 48.$$
- Thus, the average symbol error probability is equal to
- $$p_{\rm S} = { E}/{ 16} \cdot 48 p = 3p = \underline{1.2\%} \hspace{0.05cm}.$$
- The same result is obtained with the equation given in the "theory section":
- $$p_{\rm S} = 4p \cdot \left [ 1 - { 1}/{ \sqrt{M}} \right ] = 4p \cdot \left [ 1 - { 1}/{ 4} \right ] = 3p \hspace{0.05cm}.$$
- Both equations hold exactly only if one excludes diagonal falsifications as here.
(5) With Gray coding according to the red labeling in the graph, each symbol error causes exactly one bit error.
- But since with each symbol $M = 4$ binary symbols ("bits") are transmitted, the average bit error probability is
- $$p_{\rm B} = \frac{ p_{\rm S}}{ {\rm log_2} \hspace{0.05cm}(M)} = \frac{ 1.2\%}{ 4} = \underline{0.3\%} \hspace{0.05cm}.$$
