Exercise 4.2: Channel Log Likelihood Ratio at AWGN

Conditional Gaussian functions

We consider two channels $\rm A$ and $\rm B$, each with

binary bipolar input $x ∈ \{+1, \, -1\}$, and

continuous-valued output $y ∈ {\rm \mathcal{R}}$ (real number).

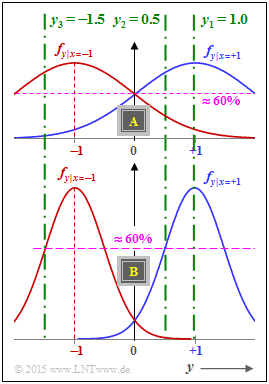
The graph shows for both channels

as blue curve the probability density functions $f_{y\hspace{0.05cm}|\hspace{0.05cm}x=+1}$,

as red curve the probability density functions $f_{y\hspace{0.05cm}|\hspace{0.05cm}x=-1}$.

In the "theory section" the channel $($German: "Kanal" ⇒ subscript: "K"$)$ log likelihood ratio was derived for this AWGN constellation as follows:

$$L_{\rm K}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=+1) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = -1)} \hspace{0.05cm}.$$

Evaluating this equation analytically, we obtain with the proportionality constant $K_{\rm L} = 2/\sigma^2$:

$$L_{\rm K}(y) = K_{\rm L} \cdot y \hspace{0.05cm}.$$

Hints:

This exercise belongs to the chapter "Soft–in Soft–out Decoder".

Reference is made in particular to the sections

"Reliability Information – Log Likelihood Ratio",

"AWGN–Channel at Binary Input".

Questions

Solution

(1) All proposed solutions are correct:

The transfer equation is always $y = x + n$, with $x ∈ \{+1, \, -1\}$.

The variable $n$ is a Gaussian random variable with standard deviation $\sigma$ ⇒ variance $\sigma^2$ ⇒ "AWGN Channel".

The "AWGN bit error probability" is calculated using the standard deviation $\sigma$ to ${\rm Q}(1/\sigma)$ where ${\rm Q}(x)$ denotes the "complementary Gaussian error function".

For each AWGN channel, according to the "theory section", the channel log likelihood ratio always results in $L_{\rm K}(y) = L(y|x) = K_{\rm L} \cdot y$.

The constant $K_{\rm L}$ is different for the two channels.

(2) For the AWGN channel ⇒ $L_{\rm K}(y) = K_{\rm L} \cdot y$ with constant $K_{\rm L} = 2/\sigma^2$.

The standard deviation $\sigma$ can be read from the graph on the data page as the distance of the inflection points within the Gaussian curves from their respective midpoints. For channel A ⇒ $\sigma = 1$ results.

The same result is obtained by evaluating the Gaussian function

$$\frac{f_{\rm G}( y = \sigma)}{f_{\rm G}( y = 0)} = {\rm e} ^{ - y^2/(2\sigma^2) } \Bigg |_{\hspace{0.05cm} y \hspace{0.05cm} = \hspace{0.05cm} \sigma} = {\rm e} ^{ -0.5} \approx 0.6065\hspace{0.05cm}.$$

This means: At the abscissa value $y = \sigma$ the mean-free Gaussian function $f_{\rm G}(y)$ has decayed to $60.65\%$ of its maximum value.

Thus, for the constant at channel A: $K_{\rm L} = 2/\sigma^2 \ \underline{= 2}$.

(3) Correct are the solutions 1 to 4:

We first give the respective log likelihood ratios of Channel A:

$$L_{\rm K}(y_1 = +1.0) = +2\hspace{0.05cm},\hspace{0.3cm} L_{\rm K}(y_2 = +0.5) = +1\hspace{0.05cm},\hspace{0.3cm} L_{\rm K}(y_3 = -1.5) = -3\hspace{0.05cm}. $$

This results in the following consequences:

The decision for the $($most probable$)$ code bit $x_i$ is based on the sign of $L_{\rm K}(y_i)$:
$x_1 = +1, \ x_2 = +1, \ x_3 = \, -1$ ⇒ the proposed solutions 1, 2 and 3 are correct.
The decision "$x_1 = +1$" is more reliable than the decision "$x_2 = +1$" ⇒ Proposition 4 is also correct.
However, the decision "$x_1 = +1$" is less reliable than the decision "$x_3 = \, –1$" because $|L_{\rm K}(y_1)<|L_{\rm K}(y_3)|$ ⇒ proposed solution 5 is incorrect.

This can also be interpreted as follows: The quotient between the red and the blue PDF value at $y_3 = \, -1.5$ is larger than the quotient between the blue and the red PDF value at $y_1 = +1$.

(4) Following the same considerations as in subtask (2), the standard deviation of channel B is given by:

$$\sigma = 1/2 \ \Rightarrow \ K_{\rm L} = 2/\sigma^2 \ \underline{= 8}.$$

(5) For channel B, the following applies:

$$L_{\rm K}(y_1 = +1.0) = +8, \ L_{\rm K}(y_2 = +0.5) = +4, \ L_{\rm K}(y_3 = \, -1.5) = \, -12.$$

It is obvious that the first two proposed solutions are true, but not the third, because

$$|L_{\rm K}(y_3 = -1.5, {\rm channel\hspace{0.15cm} A)}| = 3 \hspace{0.2cm} <\hspace{0.2cm} |L_{\rm K}(y_2 = 0.5, {\rm channel\hspace{0.15cm} B)}| = 4\hspace{0.05cm} . $$

	$y_1 = 1.0$ states that probably $x_1 = +1$ was sent.
	$y_2 = 0.5$ states that probably $x_2 = +1$ was sent.
	$y_3 = \, -1.5$ states that probably $x_3 = \, -1$ was sent.
	The decision "$y_1 → x_1$" is safer than "$y_2 → x_2$".
	The decision "$y_1 → x_1$" is safer than "$y_3 → x_3$".

	They describe the binary transmission under Gaussian noise.
	The bit error probability without coding is ${\rm Q}(1/\sigma)$.
	The channel log likelihood ratio is given as $L_{\rm K}(y) = K_{\rm L} \cdot y$.

	For $x_1, \ x_2, \ x_3$ is decided the same as for channel $\rm A$.
	The estimate "$x_2 = +1$" is four times more certain than for channel $\rm A$.
	The estimate "$x_3 = \, -1$" at channel $\rm A$ is more reliable than the estimate "$x_2 = +1$" at channel $\rm B$.