Exercise 3.5: Kullback-Leibler Distance and Binomial Distribution
We assume here the binomial distribution, which is characterised by the parameters $I$ and $p$
⇒ see the book "Theory of Stochastic Signals":
- Range of Values:
- $$X = \{\hspace{0.05cm}0\hspace{0.05cm}, \hspace{0.15cm} 1\hspace{0.05cm},\hspace{0.15cm} 2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} {\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm} , \hspace{0.15cm} I\hspace{0.05cm}\}\hspace{0.05cm},$$
- Probabilities:
- $$P_X (X = \mu) = {I \choose \mu} \cdot p^{\mu} \cdot (1-p)^{I-\mu} \hspace{0.05cm},$$
- Linear mean:
- $$m_X = I \cdot p \hspace{0.05cm},$$
- Variance:
- $$\sigma_X^2 = I \cdot p \cdot (1-p)\hspace{0.05cm}.$$
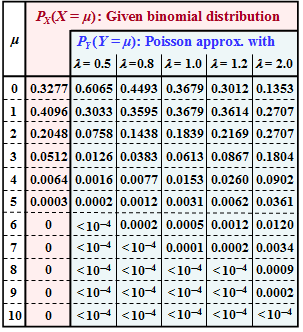
In the part of the table highlighted in red, the probabilities $P_X(X = \mu$) of the binomial distribution under consideration are given. In subtask (1) you are to determine the corresponding distribution parameters $I$ and $p$.
This given binomial distribution is to be approximated here by a Poisson distribution $Y$, characterised by the rate $\lambda$:
- Range of values:
- $$Y = \{\hspace{0.05cm}0\hspace{0.05cm}, \hspace{0.15cm} 1\hspace{0.05cm},\hspace{0.05cm} 2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} {\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm}\}\hspace{0.05cm},$$
- Probabilites:
- $$P_Y (Y = \mu) = \frac{\lambda^{\mu}}{\mu !} \cdot {\rm e}^{-\lambda} \hspace{0.05cm},$$
- Expected values:
- $$m_Y = \sigma_Y^2 = \lambda\hspace{0.05cm}.$$
In order to assess whether the probability mass function $P_X(X)$ is sufficiently well approximated by $P_Y(Y)$, one can resort to the so-called Kullback–Leibler distances $\rm (KLD)$, sometimes also called "relative entropies" in the literature.
Adapted to the present example, these are:
- $$D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) \hspace{0.15cm} = \hspace{0.15cm} {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 0}^{I} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} \hspace{0.05cm},$$
- $$D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X) \hspace{0.15cm} = \hspace{0.15cm} {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 0}^{\infty} P_Y(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_Y(\mu)}{P_X(\mu)} \hspace{0.05cm}.$$
If $\log_2$ is used, the pseudo–unit "bit" must be added to the numerical value.
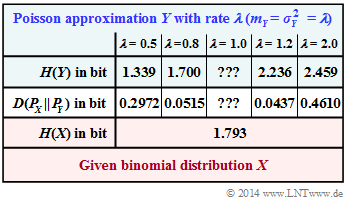
In the adjacent table, the Kullback–Leibler–distance $D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y)$ (in "bit") between the binomial PMF $P_X(\cdot)$ and some Poisson approximations $P_Y(\cdot)$ $($with five different rates $\lambda)$ is entered.
- The respective entropy $H(Y)$, which also depends on the rate $\lambda$, is given in the first row.
- The columns for $\lambda = 1$ are to be completed in subtasks (3) and (4) .
- In subtask (6) these results are to be interpreted.
Hints:
- The exercise belongs to the chapter Some preliminary remarks on two-dimensional random variables.
- In particular, reference is made to the section Relative entropy – Kullback-Leibler distance.
- To keep the numerical calculations within limits, the following auxiliary quantities are given; here $\rm \lg$ denotes the logarithm to base $10$:
- $$A\hspace{0.05cm}' = 0.4096 \cdot {\rm lg} \hspace{0.1cm} \frac{0.4096}{0.3679} + 0.2048 \cdot {\rm lg} \hspace{0.1cm} \frac{0.2048}{0.1839} + 0.0512 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0512}{0.0613} + 0.0064 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0064}{0.0153} + 0.0003 \cdot {\rm lg} \hspace{0.1cm} \frac{0.0003}{0.0031} \hspace{0.05cm},$$
- $$B\hspace{0.05cm}' = 0.1839 \cdot {\rm lg} \hspace{0.1cm} (0.1839) + 0.0613 \cdot {\rm lg} \hspace{0.1cm} (0.0613) + 0.0153 \cdot {\rm lg} \hspace{0.1cm} (0.0153) + 0.0031 \cdot {\rm lg} \hspace{0.1cm} (0.0031) + 0.0005 \cdot {\rm lg} \hspace{0.1cm} (0.0005) + 0.0001 \cdot {\rm lg} \hspace{0.1cm} (0.0001)$$
- $$\Rightarrow \hspace{0.3cm} A\hspace{0.05cm}' \hspace{0.15cm} \underline {= 0.021944} \hspace{0.05cm},\hspace{0.5cm} B\hspace{0.05cm}' \hspace{0.15cm} \underline {= -0.24717} \hspace{0.05cm}.$$
Questions
Solution
- $${\rm Pr} (X = 5) = {5 \choose 5} \cdot p^{5} = p^{5} \approx 0.0003 \hspace{0.05cm}.$$
Thus one obtains for
- the characteristic probability: $p= (0.0003)^{1/5} = 0.1974 \hspace{0.15cm} \underline {\approx 0.2}\hspace{0.05cm},$
- the linear mean (expected value): $m_X = I \cdot p \hspace{0.15cm} \underline {= 1}\hspace{0.05cm},$
- the variance: $\sigma_X^2 = I \cdot p \cdot (1-p) \hspace{0.15cm} \underline {= 0.8}\hspace{0.05cm}.$
(2) Proposed solution 2 is correct:
- Using $D(P_Y \hspace{0.05cm}|| \hspace{0.05cm} P_X)$ would always result in an infinite value regardless of $λ$ since for $\mu ≥ 6$ :
- $$P_X (X = \mu) = 0 \hspace{0.05cm},\hspace{0.3cm}P_Y (Y = \mu) \ne 0 \hspace{0.05cm}.$$
- Even though the probabilities $P_Y (Y = \mu)$ become very small for large $μ$ they are still "infinitely larger" than $P_X (X = \mu)$.
(3) We use the first Kullback–Leibler distance:
- $$D = D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) =\hspace{0.2cm} \sum_{\mu = 0}^{5} P_X(\mu) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_X(\mu)}{P_Y(\mu)} \hspace{0.05cm}.$$
- Using the logarithm of base ten $(\lg)$, we obtain for the Poisson approximation with $\lambda = 1$:
- $$D \hspace{0.05cm}' = 0.3277 \cdot {\rm lg} \hspace{0.1cm} \frac{0.3277}{0.3679} + A \hspace{0.05cm}' = -0.016468 + 0.021944 = 0.005476 \hspace{0.05cm}.$$
- After converting to the logarithm of base two $(\log_2)$ , we finally obtain:
- $$D = D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) = \frac{0.005476}{{\rm lg} \hspace{0.1cm}(2)} \hspace{0.15cm} \underline {\approx 0.0182\ {\rm (bit)}}\hspace{0.05cm}.$$
(4) Using the logarithm of base ten, the entropy of the Poisson approximation $(\lambda = 1)$:
- $$H\hspace{0.05cm}'(Y) = -{\rm E} \left [{\rm lg} \hspace{0.1cm} {P_Y(Y)} \right ] = -2 \cdot 0.3679 \cdot {\rm lg} \hspace{0.1cm} (0.3679) - B\hspace{0.05cm}' = 0.31954 + 0.24717 = 0.56126.$$
- Converting to "bit" gives the result we are looking for:
- $$H(Y) = \frac{0.56126}{{\rm lg} \hspace{0.1cm}(2)} \hspace{0.15cm} \underline {= 1.864\ {\rm (bit)}} \hspace{0.05cm}.$$
(5) Correct is statement 1. In the numerical calculation of the Kullback–Leibler distance
- the contribution of the $μ$–th term is positive, if $P_Y(\mu) > P_X(\mu)$,
- the contribution of the $μ$–th term is negative, if $P_Y(\mu) < P_X(\mu)$.
(6) Proposed solution 1 is correct:
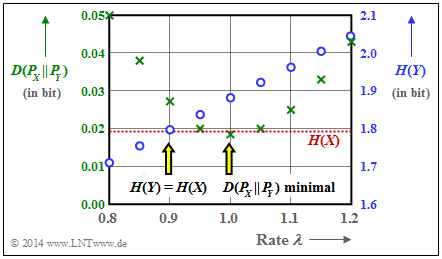
- It can also be seen from the graph that $D(P_X \hspace{0.05cm}|| \hspace{0.05cm} P_Y) =0.0182$ bit is not undercut by any $λ$–value other than $λ = 1$ (green crosses).
- Furthermore, one can see from this plot that a better entropy approximation is achieved with $λ = 0.9$ than with $λ = 1$ (blue circles):
- $$H(Y) = 1.795\ {\rm bit} \hspace{0.15cm}\approx \hspace{0.15cm} H(X) = 1.793\ {\rm bit}\hspace{0.05cm}.$$
- The second proposed solution is therefore wrong.
- With $λ = 1$ , the linear means of the two random variables coincide:
- $$m_X = m_Y= 1.$$
- With $λ = 0.9$ the second moments agree:
- $$m_X + \sigma_X^2 = m_Y + \sigma_Y^2= 1.8.$$
Whether this statement is relevant, we leave undecided.
Because: Due to the steady increase of $H(Y)$ with increasing $λ$ , it is clear that for some $λ$–value $H(Y) = H(X)$ must indeed hold.