Binomial Distribution

1. Theory of Stochastic Signals
2. Discrete Random Variable
3. Binomial Distribution

• Previous page
• Next page

• Previous page
• Next page

General description of the binomial distribution

$\text{Definition:}$  The  »binomial distribution«  represents an important special case for the occurrence probabilities of a discrete random variable.

To derive the binomial distribution,  we assume that  $I$  binary and statistically independent random variables  $b_i$  each can achieve

• the value  $1$  with probability  ${\rm Pr}(b_i = 1) = p$,  and

• the value  $0$  with probability  ${\rm Pr}(b_i = 0) = 1-p$.

Then the sum  $z$  is also a discrete random variable with the symbol set   $\{0, \ 1, \ 2,\hspace{0.1cm}\text{ ...} \hspace{0.1cm}, \ I\}$,  which is called binomially distributed:

$$z=\sum_{i=1}^{I}b_i.$$

Thus,  the symbol set size is  $M = I + 1.$

$\text{Example 1:}$  The binomial distribution finds manifold applications in Communications Engineering as well as in other disciplines:

1.   It describes the distribution of rejects in statistical quality control.
2.   It allows the calculation of the residual error probability in blockwise coding.
3.  The bit error rate of a digital transmission system obtained by simulation is actually a binomially distributed random quantity.

Probabilities of the binomial distribution

$\text{Calculation rule:}$  For the  »probabilities of the binomial distribution«  with  $μ = 0, \hspace{0.1cm}\text{...} \hspace{0.1cm}, \ I$:

$$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p\hspace{0.05cm}^\mu\cdot ({\rm 1}-p)\hspace{0.05cm}^{I-\mu}.$$

The first term here indicates the number of combinations   $($read:  $I\ \text{ over }\ μ)$:

$${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$

$\text{Additional notes:}$

1. For very large values of  $I$,  the binomial distribution can be approximated by the  »Poisson distribution«  described in the next section.
2. If at the same time the product  $I · p \gg 1$,  then according to  »de Moivre–Laplace's $($central limit$)$ theorem«,  the Poisson distribution  $($and hence the binomial distribution$)$  transitions to a discrete  »Gaussian distribution«.

Binomial distribution probabilities

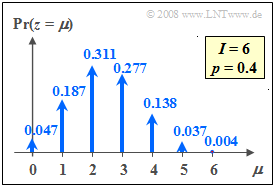
$\text{Example 2:}$  The graph shows the probabilities of the binomial distribution for  $I =6$  and  $p =0.4$. 

• Thus  $M = I+1=7$  probabilities are different from zero.

• In contrast,  for  $I = 6$  and  $p = 0.5$,  the probabilities of the binomial distribution are as follows:

$$\begin{align*}{\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}0) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}6)\hspace{-0.05cm} =\hspace{-0.05cm} 1/64\hspace{-0.05cm} = \hspace{-0.05cm}0.015625 ,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}1) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}5) \hspace{-0.05cm}= \hspace{-0.05cm}6/64 \hspace{-0.05cm}=\hspace{-0.05cm} 0.09375,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}2) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}4)\hspace{-0.05cm} = \hspace{-0.05cm}15/64 \hspace{-0.05cm}= \hspace{-0.05cm}0.234375 ,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}3) & = 20/64 \hspace{-0.05cm}= \hspace{-0.05cm} 0.3125 .\end{align*}$$

• These are symmetrical with respect to the abscissa value  $\mu = I/2 = 3$.

$\text{Example 3:}$  Another example of the application of the binomial distribution is the  »calculation of the block error probability in Digital Signal Transmission«.

If one transmits blocks each of  $I =10$  binary symbols over a channel

• with probability  $p = 0.01$  that one symbol is falsified   ⇒   random variable  $e_i = 1$,  and

• correspondingly with probability  $1 - p = 0.99$  for an unfalsified symbol   ⇒   random variable  $e_i = 0$,

then the new random variable  $f$   ⇒   »number of block errors«  is:

$$f=\sum_{i=1}^{I}e_i.$$

This random variable  $f$  can take all integer values between  $0$  $($no symbol is falsified$)$  and  $I$  $($all symbols symbol are falsified$)$ . 

1. We denote the probabilities for  $\mu$  falsifications by  $p_μ$.
2. The case where all  $I$  symbols are correctly transmitted occurs with probability  $p_0 = 0.99^{10} ≈ 0.9044$ .
3. This also follows from the binomial formula for  $μ = 0$  considering the definition  $10\, \text{ over }\, 0 = 1$.
4. A single symbol error  $(f = 1)$  occurs with the probability  $p_1 = \rm 10\cdot 0.01\cdot 0.99^9\approx 0.0914.$
5. The first factor considers that there are exactly  $10\, \text{ over }\, 1 = 10$  possibilities for the position of a single error. 
6. The other two factors take into account that one symbol must be falsified and nine must be transmitted correctly if  $f =1$  is to hold.

For  $f =2$  there are clearly more combinations,  namely  $10\, \text{ over }\, 2 = 45$,   and we get

$$p_2 = \rm 45\cdot 0.01^2\cdot 0.99^8\approx 0.0041.$$

If a block code can correct up to two errors,  the  »block error probability«  is

$$p_{\rm block} = \it p_{\rm 3} \rm +\hspace{0.1cm}\text{ ...} \hspace{0.1cm} \rm + \it p_{\rm 10}\approx \rm 10^{-4},$$

or

$$p_{\rm block} = \rm 1-\it p_{\rm 0}-\it p_{\rm 1}-p_{\rm 2}\approx \rm 10^{-4}.$$

• One can see that for large  $I$  values the second possibility of calculation via the complement leads faster to the goal.

• However,  one could also consider that for these numerical values  $p_{\rm block} ≈ p_3$  holds as an approximation.

⇒   Use the interactive HTML5/JS applet  »Binomial and Poisson distribution«  to find the binomial probabilities for any  $I$  and  $p$ .

Moments of the binomial distribution

You can calculate the moments in general using the equations in the chapters 

• »Moments of a Discrete Random Variable«,

• »Probabilities of the Binomial Distribution».

$\text{Calculation rules:}$  For the  »$k$-th order moment«  of a binomially distributed random variable,  the general rule is:

$$m_k={\rm E}\big[z^k\big]=\sum_{\mu={\rm 0} }^{I}\mu^k\cdot{I \choose \mu}\cdot p\hspace{0.05cm}^\mu\cdot ({\rm 1}-p)\hspace{0.05cm}^{I-\mu}.$$

From this,  we obtain for after some transformations

• the first order moment   ⇒   »linear mean«:

$$m_1 ={\rm E}\big[z\big]= I\cdot p,$$

• the second order moment   ⇒   »power«:

$$m_2 ={\rm E}\big[z^2\big]= (I^2-I)\cdot p^2+I\cdot p,$$

• the variance by applying »Steiner's theorem»:

$$\sigma^2 = {m_2-m_1^2} = {I \cdot p\cdot (1-p)} ,$$

• the standard deviation:

$$\sigma = \sqrt{I \cdot p\cdot (1-p)}.$$

The maximum variance  $σ^2 = I/4$  is obtained for the  »characteristic probability«  $p = 1/2$. 

• In this case,  the binomial probabilities are symmetric around the mean  $m_1 = I/2 \ ⇒ \ p_μ = p_{I–μ}$.
• The more the characteristic probability  $p$  deviates from the value  $1/2$ ,

1.   the smaller is the standard deviation  $σ$,  and
2.   the more asymmetric become the probabilities around the mean  $m_1 = I · p$.

$\text{Example 4:}$  

As in  $\text{Example 3}$,  we consider a block of  $I =10$  binary symbols,  each of which is independently falsified with probability  $p = 0.01$ .  Then holds:

• The mean number of block errors is equal to  $m_f = {\rm E}\big[ f\big] = I · p = 0.1$.

• The standard deviation of the random variable  $f$  is  $σ_f = \sqrt{0.1 \cdot 0.99}≈ 0.315$.

In contrast,  in the completely falsified channel   ⇒   bit error probability  $p = 1/2$  results in the values

• $m_f = 5$   ⇒   on average,  five of the ten bits within a block are wrong,

• $σ_f = \sqrt{I}/2 ≈1.581$   ⇒   maximum standard deviation.

Exercises for the chapter

Exercise 2.3: Algebraic Sum of Binary Numbers

Exercise 2.4: Number Lottery (6 from 49)