Contents
# OVERVIEW OF THE FIRST MAIN CHAPTER #
This first chapter describes the calculation and the meaning of entropy. According to the Shannonian information definition, entropy is a measure of the mean uncertainty about the outcome of a statistical event or the uncertainty in the measurement of a stochastic quantity. Somewhat casually expressed, the entropy of a random quantity quantifies its »randomness«.
In detail are discussed:
- The »information content« of a symbol and the »entropy« of a discrete memoryless source,
- the »binary entropy function« and its application to non-binary sources,
- the entropy calculation for »sources with memory« and suitable approximations,
- the special features of »Markov sources« regarding the entropy calculation,
- the procedure for sources with a large number of symbols, for example »natural texts«,
- the »entropy estimates« according to Shannon and Küpfmüller.
Model and requirements
We consider a discrete message source $\rm Q$, which gives a sequence $ \langle q_ν \rangle$ of symbols.
- For the variable $ν = 1$, ... , $N$, where $N$ should be sufficiently large.
- Each individual source symbol $q_ν$ comes from a symbol set $\{q_μ \}$ where $μ = 1$, ... , $M$. $M$ denotes the symbol set size:
- $$q_{\nu} \in \left \{ q_{\mu} \right \}, \hspace{0.25cm}{\rm with}\hspace{0.25cm} \nu = 1, \hspace{0.05cm} \text{ ...}\hspace{0.05cm} , N\hspace{0.25cm}{\rm and}\hspace{0.25cm}\mu = 1,\hspace{0.05cm} \text{ ...}\hspace{0.05cm} , M \hspace{0.05cm}.$$
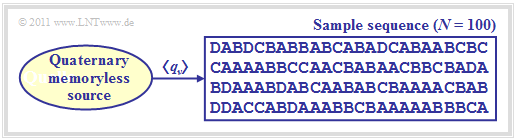
The figure shows a quaternary message source $(M = 4)$ with alphabet $\rm \{A, \ B, \ C, \ D\}$ and an exemplary sequence of length $N = 100$.
The following requirements apply:
- The quaternary source is fully described by $M = 4$ symbol probabilities $p_μ$. In general it applies:
- $$\sum_{\mu = 1}^M \hspace{0.1cm}p_{\mu} = 1 \hspace{0.05cm}.$$
- The message source is memoryless, i.e., the individual sequence elements are »statistically independent of each other«:
- $${\rm Pr} \left (q_{\nu} = q_{\mu} \right ) = {\rm Pr} \left (q_{\nu} = q_{\mu} \hspace{0.03cm} | \hspace{0.03cm} q_{\nu -1}, q_{\nu -2}, \hspace{0.05cm} \text{ ...}\hspace{0.05cm}\right ) \hspace{0.05cm}.$$
- Since the alphabet consists of symbols $($and not of random variables$)$, the specification of »expected values« $($linear mean, second moment, standard deviation, etc.$)$ is not possible here, but also not necessary from an information-theoretical point of view.
These properties will now be illustrated with an example.
$\text{Example 1:}$ For the symbol probabilities of a quaternary source applies:
- $$p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.1\hspace{0.05cm}.$$
For an infinitely long sequence $(N \to \infty)$
- the »relative frequencies« $h_{\rm A}$, $h_{\rm B}$, $h_{\rm C}$, $h_{\rm D}$ ⇒ a-posteriori parameters
- were identical to the »probabilities« $p_{\rm A}$, $p_{\rm B}$, $p_{\rm C}$, $p_{\rm D}$ ⇒ a-priori parameters.
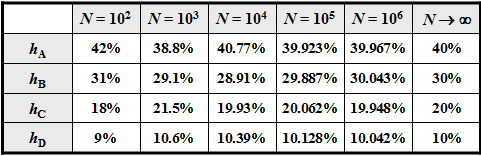
With smaller $N$ deviations may occur, as the adjacent table $($result of a simulation$)$ shows.
- In the graphic above an exemplary sequence is shown with $N = 100$ symbols.
- Due to the set elements $\rm A$, $\rm B$, $\rm C$ and $\rm D$ no mean values can be given.
However, if you replace the symbols with numerical values, for example $\rm A \Rightarrow 1$, $\rm B \Rightarrow 2$, $\rm C \Rightarrow 3$, $\rm D \Rightarrow 4$, then you will get after
»time averaging« ⇒ crossing line or »ensemble averaging« ⇒ expected value formation
- for the »linear mean« ⇒ »first order moment«:
- $$m_1 = \overline { q_{\nu} } = {\rm E} \big [ q_{\mu} \big ] = 0.4 \cdot 1 + 0.3 \cdot 2 + 0.2 \cdot 3 + 0.1 \cdot 4 = 2 \hspace{0.05cm},$$
- for the »second order moment«:
- $$m_2 = \overline { q_{\nu}^{\hspace{0.05cm}2} } = {\rm E} \big [ q_{\mu}^{\hspace{0.05cm}2} \big ] = 0.4 \cdot 1^2 + 0.3 \cdot 2^2 + 0.2 \cdot 3^2 + 0.1 \cdot 4^2 = 5 \hspace{0.05cm},$$
- for the »standard deviation« according to the »Theorem of Steiner«:
- $$\sigma = \sqrt {m_2 - m_1^2} = \sqrt {5 - 2^2} = 1 \hspace{0.05cm}.$$
Maximum entropy of a discrete source
$\text{Claude Elwood Shannon}$ defined in 1948 in the standard work of information theory [Sha48][1] the concept of information as "decrease of uncertainty about the occurrence of a statistical event".
Let us make a mental experiment with $M$ possible results, which are all equally probable: $p_1 = p_2 = \hspace{0.05cm} \text{ ...}\hspace{0.05cm} = p_M = 1/M \hspace{0.05cm}.$
Under this assumption applies:
- Is $M = 1$, then each individual attempt will yield the same result and therefore there is no uncertainty about the output.
- On the other hand, an observer learns about an experiment with $M = 2$, for example the »coin toss« with the set of events $\big \{\rm \boldsymbol{\rm Z}(ahl), \rm \boldsymbol{\rm W}(app) \big \}$ and the probabilities $p_{\rm Z} = p_{\rm W} = 0. 5$, a gain in information. The uncertainty regarding $\rm Z$ resp. $\rm W$ is resolved.
- In the experiment »dice« $(M = 6)$ and even more in »roulette« $(M = 37)$ the gained information is even more significant for the observer than in the »coin toss« when he learns which number was thrown or which ball fell.
- Finally it should be considered that the experiment »triple coin toss« with $M = 8$ possible results $\rm ZZZ$, $\rm ZZW$, $\rm ZWZ$, $\rm ZWW$, $\rm WZZ$, $\rm WZW$, $\rm WWZ$, $\rm WWW$ provides three times the information as the single coin toss $(M = 2)$.
The following definition fulfills all the requirements listed here for a quantitative information measure for equally probable events, indicated only by the symbol set size $M$.
$\text{Definition:}$ The »maximum average information content« of a message source depends only on the symbol set size $M$ and results in
- $$H_0 = {\rm log}\hspace{0.1cm}M = {\rm log}_2\hspace{0.1cm}M \hspace{0.15cm} {\rm (in \ “bit")} = {\rm ln}\hspace{0.1cm}M \hspace{0.15cm}\text {(in “nat")} = {\rm lg}\hspace{0.1cm}M \hspace{0.15cm}\text {(in “Hartley")}\hspace{0.05cm}.$$
- Since $H_0$ indicates the maximum value of the $\text{entropy}$ $H$, $H_\text{max}=H_0$ is also used in our tutorial as short notation.
Please note our nomenclature:
- The logarithm will be called »log« in the following, independent of the base.
- The relations mentioned above are fulfilled due to the following properties:
- $${\rm log}\hspace{0.1cm}1 = 0 \hspace{0.05cm},\hspace{0.2cm} {\rm log}\hspace{0.1cm}37 > {\rm log}\hspace{0.1cm}6 > {\rm log}\hspace{0.1cm}2\hspace{0.05cm},\hspace{0.2cm} {\rm log}\hspace{0.1cm}M^k = k \cdot {\rm log}\hspace{0.1cm}M \hspace{0.05cm}.$$
- Usually we use the logarithm to the base $2$ ⇒ »logarithm dualis« $\rm (ld)$, where the pseudo unit "bit" $($more precisely: "bit/symbol"$)$ is then added:
- $${\rm ld}\hspace{0.1cm}M = {\rm log_2}\hspace{0.1cm}M = \frac{{\rm lg}\hspace{0.1cm}M}{{\rm lg}\hspace{0.1cm}2} = \frac{{\rm ln}\hspace{0.1cm}M}{{\rm ln}\hspace{0.1cm}2} \hspace{0.05cm}.$$
- In addition, you can find in the literature some additional definitions, which are based on the natural logarithm $\rm (ln)$ or the logarithm of the tens $\rm (lg)$.
Information content and entropy
We now waive the previous requirement that all $M$ possible results of an experiment are equally probable. In order to keep the spelling as compact as possible, we define for this section only:
- $$p_1 > p_2 > \hspace{0.05cm} \text{ ...}\hspace{0.05cm} > p_\mu > \hspace{0.05cm} \text{ ...}\hspace{0.05cm} > p_{M-1} > p_M\hspace{0.05cm},\hspace{0.4cm}\sum_{\mu = 1}^M p_{\mu} = 1 \hspace{0.05cm}.$$
We now consider the »information content« of the individual symbols, where we denote the "logarithm dualis" with $\log_2$:
- $$I_\mu = {\rm log_2}\hspace{0.1cm}\frac{1}{p_\mu}= -\hspace{0.05cm}{\rm log_2}\hspace{0.1cm}{p_\mu} \hspace{0.5cm}{\rm (unit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}or\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
You can see:
- Because of $p_μ ≤ 1$ the information content is never negative. In the borderline case $p_μ \to 1$ goes $I_μ \to 0$.
- However, for $I_μ = 0$ ⇒ $p_μ = 1$ ⇒ $M = 1$ the information content is also $H_0 = 0$.
- For decreasing probabilities $p_μ$ the information content increases continuously:
- $$I_1 < I_2 < \hspace{0.05cm} \text{ ...}\hspace{0.05cm} < I_\mu <\hspace{0.05cm} \text{ ...}\hspace{0.05cm} < I_{M-1} < I_M \hspace{0.05cm}.$$
$\text{Conclusion:}$ The more improbable an event is, the greater is its information content. This fact is also found in daily life:
- "6 right ones" in the lottery are more likely to be noticed than "3 right ones" or no win at all.
- A tsunami in Asia also dominates the news in Germany for weeks as opposed to the almost standard Deutsche Bahn delays.
- A series of defeats of Bayern Munich leads to huge headlines in contrast to a winning series. With 1860 Munich exactly the opposite is the case.
However, the information content of a single symbol (or event) is not very interesting. On the other hand one of the central quantities of information theory is obtained,
- by ensemble averaging over all possible symbols $q_μ$ bzw.
- by time averaging over all elements of the sequence $\langle q_ν \rangle$.
$\text{Definition:}$ The »entropy« $H$ of a discrete source indicates the »mean information content of all symbols«:
- $$H = \overline{I_\nu} = {\rm E}\hspace{0.01cm}[I_\mu] = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{p_\mu}= -\sum_{\mu = 1}^M p_{\mu} \cdot{\rm log_2}\hspace{0.1cm}{p_\mu} \hspace{0.5cm}\text{(unit: bit, more precisely: bit/symbol)} \hspace{0.05cm}.$$
The overline marks again a time averaging and $\rm E[\text{...}]$ an ensemble averaging.
Entropy is among other things a measure for
- the mean uncertainty about the outcome of a statistical event,
- the "randomness" of this event, and
- the average information content of a random variable.
Binary entropy function
At first we will restrict ourselves to the special case $M = 2$ and consider a binary source, which returns the two symbols $\rm A$ and $\rm B$. The symbol probabilities are $p_{\rm A} = p$ and $p_{\rm B} = 1 - p$.
For the entropy of this binary source applies:
- $$H_{\rm bin} (p) = p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1-p} \hspace{0.5cm}{\rm (unit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}or\hspace{0.15cm}bit/symbol)} \hspace{0.05cm}.$$
This function is called $H_\text{bin}(p)$ the »binary entropy function«. The entropy of a source with a larger symbol set size $M$ can often be expressed using $H_\text{bin}(p)$ .
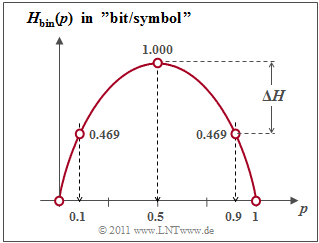
$\text{Example 2:}$ The figure shows the binary entropy function for the values $0 ≤ p ≤ 1$ of the symbol probability of $\rm A$ $($or also of $\rm B)$. You can see:
- The maximum value $H_\text{max} = 1\; \rm bit$ results for $p = 0.5$, thus for equally probable binary symbols. Then $\rm A$ and $\rm B$ contribute the same amount to the entropy.
- $H_\text{bin}(p)$ is symmetrical around $p = 0.5$. A source with $p_{\rm A} = 0.1$ and $p_{\rm B} = 0. 9$ has the same entropy $H = 0.469 \; \rm bit$ as a source with $p_{\rm A} = 0.9$ and $p_{\rm B} = 0.1$.
- The difference $ΔH = H_\text{max} - H$ gives the »redundancy« of the source and $r = ΔH/H_\text{max}$ the »relative redundancy«. In the example, $ΔH = 0.531\; \rm bit$ and $r = 53.1 \rm \%$.
- For $p = 0$ this results in $H = 0$, since the symbol sequence $\rm B \ B \ B \text{...}$ can be predicted with certainty ⇒ symbol set size only $M = 1$. The same applies to $p = 1$ ⇒ symbol sequence $\rm A \ A \ A \text{...}$.
- $H_\text{bin}(p)$ is always a »concave function«, since the second derivative after the parameter $p$ is negative for all values of $p$ :
- $$\frac{ {\rm d}^2H_{\rm bin} (p)}{ {\rm d}\,p^2} = \frac{- 1}{ {\rm ln}(2) \cdot p \cdot (1-p)}< 0 \hspace{0.05cm}.$$
Non-binary sources
In the "first section" of this chapter we considered a quaternary message source $(M = 4)$ with the symbol probabilities $p_{\rm A} = 0. 4$, $p_{\rm B} = 0.3$, $p_{\rm C} = 0.2$ and $ p_{\rm D} = 0.1$. This source has the following entropy:
- $$H_{\rm quat} = 0.4 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.4} + 0.3 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0. 3} + 0.2 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.2}+ 0.1 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.1}.$$
For numerical calculation, the detour via the decimal logarithm $\lg \ x = {\rm log}_{10} \ x$ is often necessary, since the "logarithm dualis" $ {\rm log}_2 \ x$ is mostly not found on pocket calculators.
- $$H_{\rm quat}=\frac{1}{{\rm lg}\hspace{0.1cm}2} \cdot \left [ 0.4 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.4} + 0.3 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0. 3} + 0.2 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.2} + 0.1 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.1} \right ] = 1.845\,{\rm bit} \hspace{0.05cm}.$$
$\text{Example 3:}$ Now there are certain symmetries between the symbol probabilities:
- $$p_{\rm A} = p_{\rm D} = p \hspace{0.05cm},\hspace{0.4cm}p_{\rm B} = p_{\rm C} = 0.5 - p \hspace{0.05cm},\hspace{0.3cm}{\rm with} \hspace{0.15cm}0 \le p \le 0.5 \hspace{0.05cm}.$$
In this case, the binary entropy function can be used to calculate the entropy:
- $$H_{\rm quat} = 2 \cdot p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm} } + 2 \cdot (0.5-p) \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.5-p}$$
$$\Rightarrow \hspace{0.3cm} H_{\rm quat} = 1 + H_{\rm bin}(2p) \hspace{0.05cm}.$$
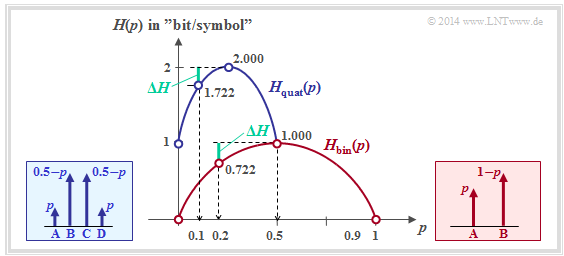
The graphic shows as a function of $p$
- the entropy of the quaternary source (blue)
- in comparison to the entropy course of the binary source (red).
For the quaternary source only the abscissa $0 ≤ p ≤ 0.5$ is allowed.
⇒ You can see from the blue curve for the quaternary source:
- The maximum entropy $H_\text{max} = 2 \; \rm bit/symbol$ results for $p = 0.25$ ⇒ equally probable symbols: $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm A} = 0.25$.
- With $p = 0$ the quaternary source degenerates to a binary source with $p_{\rm B} = p_{\rm C} = 0. 5$, $p_{\rm A} = p_{\rm D} = 0$ ⇒ $H = 1 \; \rm bit/symbol$. Similar applies to $p = 0.5$.
- The source with $p_{\rm A} = p_{\rm D} = 0.1$ and $p_{\rm B} = p_{\rm C} = 0.4$ has the following characteristics (each with the pseudo unit "bit/symbol"):
- (1) entropy: $H = 1 + H_{\rm bin} (2p) =1 + H_{\rm bin} (0.2) = 1.722,$
- (2) Redundancy: ${\rm \Delta }H = {\rm log_2}\hspace{0.1cm} M - H =2- 1.722= 0.278,$
- (3) relative redundancy: $r ={\rm \Delta }H/({\rm log_2}\hspace{0.1cm} M) = 0.139\hspace{0.05cm}.$
- The redundancy of the quaternary source with $p = 0.1$ is $ΔH = 0.278 \; \rm bit/symbol$ ⇒ exactly the same as the redundancy of the binary source with $p = 0.2$.
Exercises for the chapter
Exercise 1.1: Entropy of the Weather
Exercise 1.1Z: Binary Entropy Function
Exercise 1.2: Entropy of Ternary Sources
References
- ↑ Shannon, C.E.: A Mathematical Theory of Communication. In: Bell Syst. Techn. J. 27 (1948), pp. 379-423 and pp. 623-656.