Analytical Signal and its Spectral Function

Definition in the frequency domain

We consider a real band-pass signal $x(t)$ with the corresponding band-pass spectrum $X(f)$, which has an even real and an odd imaginary part with respect to the frequency zero point. It is assumed that the carrier frequency $f_{\rm T}$ is much larger than the bandwidth of the band-pass signal $x(t)$.

$\text{Definition:}$ The »analytical signal« $x_+(t)$ belonging to the physical signal $x(t)$ is that time function, whose spectrum fulfills the following property:

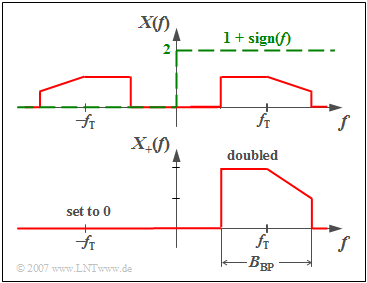
Analytical signal in the frequency domain

$$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot X(f) \; \hspace{0.2cm}\rm for\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm for\hspace{0.2cm} {\it f} < 0.} }\right.$$

The »sign function« is equal to $+1$ for positive $f$–values and for negative $f$-values equal to $-1$.

The $($double sided$)$ limit value returns $\sign(0) = 0$.

The index "+" should make clear that $X_+(f)$ has only parts at positive frequencies.

From the graphic you can see the calculation rule for $X_+(f)$: The actual band-pass spectrum $X(f)$ will

be doubled at the positive frequencies, and

set to zero at the negative frequencies.

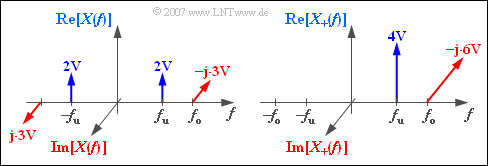
$\text{Example 1:}$ The graph

Spectrum $X(f)$ and Spectrum $X_{+}(f)$ of the analytical signal

on the left shows the $($discrete and complex$)$ spectrum $X(f)$ of the "physical band-pass signal"

$$x(t) = 4\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi f_{\rm u} \hspace{0.03cm}t) + 6\hspace{0.05cm}{\rm V} \cdot {\sin} ( 2 \pi f_{\rm o} \hspace{0.03cm}t),$$

on the right the $($also discrete and complex$)$ spectrum $X_{+}(f)$ of the corresponding "analytical signal" $x_{+}(t)$.

General calculation rule in the time domain

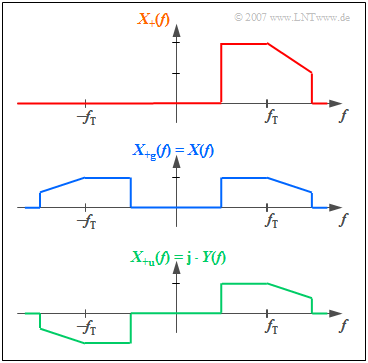
Now we will take a closer look at the spectrum $X_+(f)$ of the analytical signal and divide it with respect to $f = 0$ into

For a clear explanation of the analytical signal

an even $($German: "gerade" ⇒ "$\rm g"$) part $X_{\rm +g}(f)$, and

an odd $($German: "ungerade" ⇒ "$\rm u$") part $X_{\rm +u}(f)$:

$$X_+(f) = X_{\rm +g}(f) + X_{\rm +u}(f).$$

All these spectra are generally complex.

If one considers the »Assignment Theorem« of the Fourier transform, then the following statements are possible on basis of the graph:

The even part $X_{\rm +g}(f)$ of $X_{+}(f)$ leads after the Fourier transform to a real time signal, and the odd part $X_{\rm +u}(f)$ to an imaginary one.

It is obvious that $X_{\rm +g}(f)$ is equal to the physical Fourier spectrum $X(f)$ and thus the real part of $x_{\rm +g}(t)$ is equal to the given physical signal $x(t)$ with band-pass properties.

If we denote the imaginary part with $y(t)$, the analytical signal is:

$$x_+(t)= x(t) + {\rm j} \cdot y(t) .$$

According to the generally valid laws of Fourier transform corresponding to the »Assignment Theorem«, the following applies to the spectral function of the imaginary part:

$${\rm j} \cdot Y(f) = X_{\rm +u}(f)= {\rm sign}(f) \cdot X(f) \hspace{0.3cm}\Rightarrow\hspace{0.3cm}Y(f) = \frac{{\rm sign}(f)}{ {\rm j}}\cdot X(f).$$

After transforming this equation into the time domain, the multiplication becomes the »convolution«, and one gets:

$$y(t) = \frac{1}{ {\rm \pi} t} \hspace{0.05cm}\star \hspace{0.05cm}x(t) = \frac{1}{ {\rm \pi}} \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - \tau}}\hspace{0.15cm} {\rm d}\tau.$$

Representation with Hilbert transform

At this point it is necessary to briefly discuss a further spectral transformation, which is dealt thoroughly in the book »Linear and Time-invariant Systems« .

$\text{Definition:}$ For the »Hilbert transform« $ {\rm H}\left\{x(t)\right\}$ of a time function $x(t)$ applies:

$$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - \tau} }\hspace{0.15cm} {\rm d}\tau.$$

This particular integral cannot be solved in a simple, conventional way, but must be evaluated using the »Cauchy principal value«.

Correspondingly valid in the frequency domain:

$$Y(f) = - {\rm j} \cdot {\rm sign}(f) \cdot X(f) \hspace{0.05cm} .$$

Thus, the result of the last section can be summarized with this definition as follows:

You get from the real, physical band-pass signal $x(t)$ the analytic signal $x_+(t)$ by adding to $x(t)$ an imaginary part according to the Hilbert transform:

$$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$

The Hilbert transform $\text{H}\{x(t)\}$ disappears only in the case of $x(t) = \rm const.$ ⇒ DC signal. With all other signal forms the analytic signal $x_+(t)$ is always complex.

From the analytical signal $x_+(t)$ the real band-pass signal can be easily determined by real part formation:

$$x(t) = {\rm Re}\left\{x_+(t)\right\} .$$

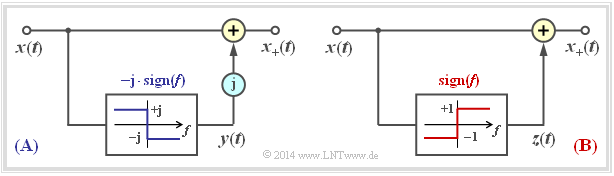
$\text{Example 2:}$ The principle of the Hilbert transformation is illustrated here by the following diagram:

According to the left representation $\rm (A)$, one gets the analytical signal $x_+(t)$ from the physical signal $x(t)$ by adding an imaginary part ${\rm j} \cdot y(t)$.

Here, $y(t) = {\rm H}\left\{x(t)\right\}$ is a real time function, which can be calculated easily in the spectral domain by multiplying the spectrum $X(f)$ with $- {\rm j} \cdot \sign(f)$.

Illustration of the Hilbert transform

The right representation $\rm (B)$ is equivalent to $\rm (A)$:

With the imaginary function $z(t)$ one obtains:

$$x_+(t) = x(t) + z(t).$$

A comparison of both models shows that it is indeed true:

$$z(t) = {\rm j} \cdot y(t).$$

Pointer diagram representation of the harmonic oscillation

The spectral function $X(f)$ of a harmonic oscillation $x(t) = A \cdot \text{cos}(2\pi f_{\rm T}t - \varphi)$ consists of two Dirac delta functions at frequencies

$+f_{\rm T}$ with complex weight $A/2 \cdot \text{e}^{-\text{j}\hspace{0.05cm}\varphi}$,

$-f_{\rm T}$ with complex weight $A/2 \cdot \text{e}^{+\text{j}\hspace{0.05cm}\varphi}$.

Thus, the spectrum of the analytical signal is $($without the Dirac delta function at the frequency $f =-f_{\rm T})$:

$$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm T}) .$$

The corresponding time function is obtained by applying the »Shifting Theorem«:

$$x_+(t) = A \cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}( 2 \pi f_{\rm T} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$

This equation describes a rotating pointer with constant angular velocity $\omega_{\rm T} = 2\pi f_{\rm T}$.

In the following, we will also refer to the time course of an analytical and frequency-discrete signal $x_+(t)$ as »pointer diagram«.

$\text{Example 3:}$ For illustrative reasons the coordinate system here is rotated $($real part upwards, imaginary part to the left$)$, contrary to the usual representation by $90^\circ$.

Pointer diagram of a harmonic oscillation

On the basis of this diagram the following statements are possible:

At the start time $t = 0$ the pointer of length $A$ $($amplitude$)$ lies with angle $-\varphi$ in the complex plane. In the drawn example, $\varphi = 45^\circ$.

For times $t > 0$ the pointer rotates with constant angular velocity $($circular frequency$)$ $\omega_{\rm T}$ in mathematically positive direction, i.e. counterclockwise.

The top of the pointer thus always lies on a circle with radius $A$ and requires exactly the time $T_0$, i.e. the »period duration« of the harmonic oscillation $x(t)$ for one rotation.

The projection of the analytical signal $x_+(t)$ onto the real axis, marked by red dots, provides the instantaneous values of $x(t)$.

Pointer diagram of a sum of harmonic oscillations

For the further description we assume the following spectrum for the analytical signal:

Pointer diagram of a sum of three oscillations

$$X_+(f) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} \varphi_i}\cdot\delta (f - f_{i}) .$$

The left graphic shows such a spectrum for the example $I = 3$.
If one chooses $I$ relatively large and the distance between adjacent spectral lines correspondingly small, then with this equation frequency–continuous spectral functions $X_+(f)$ can also be approximated.

In the right graphic the corresponding time function is indicated. This is in general:

$$x_+(t) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}(\omega_i \hspace{0.05cm}\cdot\hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$

To note about this graphic:

The sketch shows the initial position of the pointers at start time $t = 0$ corresponding to the amplitudes $A_i$ and the phase positions $\varphi_i$.

The tip of the resulting pointer compound is marked by the violet cross. One obtains by vectorial addition of the three individual pointers for the time $t = 0$:

$$x_+(t= 0) = \big [1 \cdot \cos(60^\circ) - 1 \cdot {\rm j} \cdot \sin(60^\circ) \big ]+ 2 \cdot \cos(0^\circ)+1 \cdot \cos(180^\circ) = 1.500 - {\rm j} \cdot 0.866.$$

For times $t > 0$ the three pointers rotate at different angular velocities $\omega_i = 2\pi f_i$. The red pointer rotates faster than the green one, but slower than the blue one.

Since all pointers rotate counterclockwise, the resulting pointer $x_+(t)$ will also tend to move in this direction.

At time $t = 1\,µ\text {s}$ the tip of the resulting pointer for the given parameter values is

$$ \begin{align*}x_+(t = 1 {\rm \hspace{0.05cm}µ s}) & = 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}60^\circ}\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}40 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001} + 2\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}50 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001}- 1\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}60 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001} = \\ & = 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}45.6^\circ} + 2\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}18^\circ}- 1\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}21.6^\circ} \approx 1.673- {\rm j} \cdot 0.464.\end{align*}$$