Conclusions from the Allocation Theorem

# OVERVIEW OF THE THIRD MAIN CHAPTER #

In the first two chapters, filter functions with real-valued frequency responses were mostly considered for reasons of presentation so that the associated time function is symmetric about zero-time.

However, the impulse response of a realizable system must always be causal, that is, $h(t)$ must be identical to zero for $t < 0$.

This strong asymmetry of the time function $h(t)$ implies at the same time that with exception of $H(f) = K$ the frequency response $H(f)$ of a realizable system is always complex-valued where there is a fixed relation between its real part and imaginary part.

This third chapter provides a recapitulatory account of the description of causal realizable systems, which differ also in the mathematical methods from those commonly used with non-causal systems.

In detail, the following is dealt with:

The »Hilbert transform«, which states how real and imaginary parts of $H(f)$ are related,
the »Laplace transform«, which yields another spectral function $H_{\rm L}(p)$ for acausal $h(t)$,
the description of realizable systems by the »pole-zero plot«, as well as
the »inverse Laplace transform« using the function theory $($»residue theorem«$)$.

For this chapter, we recommend two of our multimedia offerings:

the $($German language$)$ learning video "Rechnen mit komplexen Zahlen" ⇒ "Arithmetic operations involving complex numbers",

the $($German language$)$ interactive SWF applet "Kausale Systeme - Laplacetransformation" ⇒ "Causal systems – Laplace transform".

Prerequisites for the entire third main chapter

In the first two chapters, mostly real »transfer functions« $H(f)$ were considered for which the associated impulse response $h(t)$ is consequently always symmetric with respect to the reference time $t = 0$. Such transfer functions

are suitable to explain basic relationships in a simple way,

but unfortunately are not realizable for reasons of causality.

This becomes clear if the definition of the impulse response is considered:

$\text{Definition:}$ The »impulse response« $h(t)$ is equal to the output signal $y(t)$ of the system if an infinitely short impulse with an infinitely large amplitude is applied to the input at time $t = 0$ : $x(t) = δ(t)$. Such an impulse is called a »Dirac delta impulse«.

It is obvious that no impulse response can be realized for which $h(t < 0) ≠ 0$ holds.

$\text{Definition:}$ For a »causal system« the impulse response $h(t)$ is identical to zero for all times $t < 0$.

The only real transfer function that satisfies the causality condition »the output signal cannot start before the input signal« is:

$$H(f) = K \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h(t) = K \cdot \delta(t).$$

All other real-valued transfer functions $H(f)$ describe non-causal systems and thus cannot be realized by an $($electrical$)$ circuit network.

$\text{In other words:}$ Except for the transfer function $H(f) = K,$ any realistic transfer function is complex.

If $K=1$ holds additionally, the transfer function is said to be »ideal«.

Then, the output signal $y(t)$ is identical to the input signal $x(t)$ – even without attenuation or amplification.

Real and imaginary part of a causal transfer function

Any causal impulse response $h(t)$ can be represented as the sum

of an even (German: "gerade" ⇒ "g") part $h_{\rm g}(t)$
and an odd (German: "ungerade" ⇒ "u") part $h_{\rm u}(t)$:

$$\begin{align*} h_{ {\rm g}}(t) & = {1}/{2}\cdot \big[ h(t) + h(-t) \big]\hspace{0.05cm},\\ h_{ {\rm u}}(t) & = {1}/{2}\cdot \big[ h(t) - h(-t) \big] = h_{ {\rm g}}(t) \cdot {\rm sign}(t)\hspace{0.05cm} .\end{align*}$$

Here, the so-called »sign function« is used:

$${\rm sign}(t) = \left\{ \begin{array}{c} -1 \\ +1 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} { t < 0,} \\ { t > 0.} \\ \end{array}$$

$\text{Example 1:}$ The graph shows this splitting for a causal exponentially decreasing impulse response of a low-pass filter of first-order corresponding to $\text{Exercise 1.3Z}$:

Splitting of the impulse response into an even part and an odd part

$$h(t) = \left\{ \begin{array}{c} 0 \\ 0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad \begin{array}{c} {\rm{for} } \\ {\rm{for} } \\ {\rm{for} } \end{array}\begin{array}{*{20}c} { t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$

It can be seen that

$h_{\rm g}(t) = h_{\rm u}(t) = h(t)/2$ holds for positive times,

$h_{\rm g}(t)$ and $h_{\rm u}(t)$ differ only by the sign for negative times,

$h(t) = h_{\rm g}(t) + h_{\rm u}(t)$ holds for all times, also at time $t = 0$ $($marked by circles$)$.

Let us now consider the same issue in the spectral domain. According to the »Assignment Theorem« the following holds for the complex transfer function:

$$H(f) = {\rm Re} \left\{ H(f) \right \} + {\rm j} \cdot {\rm Im} \left\{ H(f) \right \} ,$$

where the following assignment is valid:

$${\rm Re} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm g}}(t)\hspace{0.05cm},$$

$${\rm j} \cdot {\rm Im} \left\{ H(f) \right\} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm u}}(t)\hspace{0.05cm}.$$

First, this relationship between real part and imaginary part of $H(f)$ shall be worked out using another example.

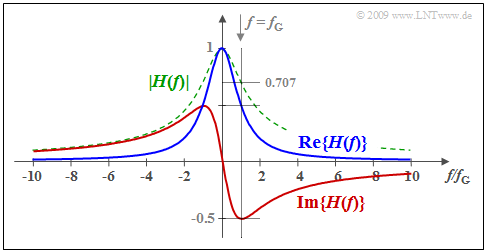
$\text{Example 2:}$ A low-pass filter of first-order is assumed and the following holds for its transfer function:

$$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G} } = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$

Frequency response of a first-order low-pass filter

Here, $f_{\rm G}$ represents the $\rm 3\hspace{0.05cm}dB$ cut-off frequency at which $\vert H(f)\vert^2$ has decreased to half of its maximum $($at $f = 0)$. The corresponding impulse response $h(t)$ has already been shown in $\text{Example 1}$ for $f_{\rm G} = 1/(2πT)$.

⇒ The graph shows the real part $($blue$)$ and the imaginary part $($red$)$ of $H(f)$. In addition, the magnitude is shown dashed in green.

Since the time functions $h_{\rm g}(t)$ and $h_{\rm u}(t)$ are related by the sign function, there also exists a fixed relationship

between the real part ⇒ ${\rm Re} \{H(f)\}$

and the imaginary part ⇒ ${\rm Im} \{H(f)\}$

of the transfer function ${\cal H} \{H(f)\}$ ⇒ »Hilbert transform«.

This is described below.

Hilbert transform

Here, two time functions $u(t)$ and $w(t) = \sign(t) · u(t)$ are considered in the most general sense:

The associated spectral functions are denoted by $U(f)$ and ${\rm j} · W(f)$.

That is: In this section ${w(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {\rm j} \cdot W(f) }$ is valid and not the usual Fourier correspondence ${w(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, W(f)}.$

Using the correspondence ${\rm sign}(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {1}/({{\rm j} \, \pi f })$ the following is obtained after writing the »convolution integral« out in full with the integration variable $ν$ :

$${\rm j} \cdot W(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, U(f) \quad \Rightarrow \quad W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

However, since at the same time also holds $u(t) = \sign(t) · w(t)$, the following is valid in the same way:

$$U(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, {\rm j} \cdot W(f) \quad \Rightarrow \quad U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

These »integral transformations« are named after their discoverer $\text{David Hilbert}$.

$\text{Definitions:}$ Both variants of the »Hilbert transformation« will be denoted by the following abbreviations in the further course:

$$W(f) \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad U(f) \hspace{0.8cm}{\rm or}\hspace{0.8cm}W(f)= {\cal H}\left\{U(f) \right \}\hspace{0.05cm}.$$

To calculate the spectrum marked by the arrowhead – here $U(f)$ – the equation with the positive sign is taken from the two otherwise identical upper equations:

$$U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

The spectrum marked by the circle – here $W(f)$ – arises as a result from the equation with the negative sign:

$$ W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu} }\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

Applying the Hilbert transformation twice yields the original function with a change of sign, and applying it four times yields the original function including the correct sign:

$${\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} = -U(f),$$

$${\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} \right \} \right \}= U(f)\hspace{0.05cm}.$$

$\text{Example 3:}$ In [Mar94]^[1] the following Hilbert correspondence can be found:

$$\frac{1}{1+x^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{x}{1+x^2}\hspace{0.05cm}.$$

Here, $x$ is representative of a suitably normalized time or frequency variable.

For example, if we use $x = f/f_{\rm G}$ as a normalized frequency variable, then we obtain the correspondence:

$$\frac{1}{1+(f/f_{\rm G})^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$

Based on the equation

$${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}$$

the result found in $\text{Example 2}$ is thus confirmed:

$${\rm Im} \left\{ H(f) \right \} = \frac{-f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$

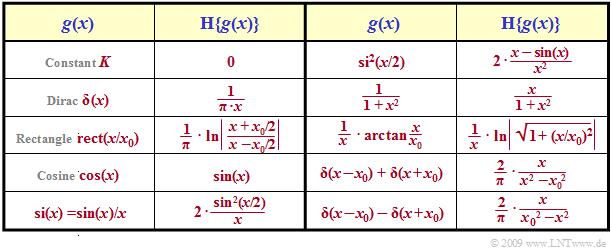
Some pairs of Hilbert correspondences

A very pragmatic way is followed to derive Hilbert correspondences, namely as follows:

The »Laplace transform« $Y_{\rm L}(p)$ of function $y(t)$ is computed as described in chapter »Laplace Transform and p-Transfer Function«. This is already implicitly causal.

$Y_{\rm L}(p)$ is converted into the associated Fourier spectrum $Y(f)$ which is split into real and imaginary part. To do this, the variable $p$ is replaced by ${\rm j \cdot 2}πf.$

Table with Hilbert correspondences

The real and imaginary parts – so ${\rm Re} \{Y(f)\}$ and ${\rm Im} \{Y(f)\}$ – are thus a pair of Hilbert transforms. Furthermore,

the frequency variable $f$ is substituted by $x$,
the real part ${\rm Re} \{Y(f)\}$ by $g(x)$, and
the imaginary part ${\rm Im} \{Y(f)\}$ by ${\cal H} \{g(x)\}$.

The new variable $x$ can describe both

a $($suitably$)$ normalized frequency

or a $($suitably$)$ normalized time.

Hence, the »Hilbert transformation« is applicable to various problems. The table shows some of such Hilbert pairs. The signs have been omitted so that both directions are valid.

$\text{Example 4:}$ For example, if ${\cal H} \{g(x)\} = f(x)$ holds, then from this it also follows that

$${\cal H} \{f(x)\} = \, –g(x).$$

In particular, it also holds:

$${\cal H}\left \{ \cos(x) \right\} = \sin(x)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\cal H}\left \{ \sin(x) \right\} = -\cos(x)\hspace{0.05cm}.$$

Attenuation and phase of minimum-phase systems

An important application of the Hilbert transformation is the relationship between attenuation and phase in so-called »minimum-phase systems«.

In anticipation of the following chapter »Laplace Transform and p-Transfer Function«, it should be mentioned that these systems may have neither poles nor zeros in the right $p$–half plane.

In general, the following holds for the transfer function $H(f)$ with

the »complex transmission function« $g(f)$
the attenuation function $a(f)$ and
the phase function $b(f)$:

$$H(f) = {\rm e}^{-g(f)} = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} g(f) = a(f)+ {\rm j} \cdot b(f)\hspace{0.05cm}.$$

Now in the case of minimum-phase systems, the Hilbert transformation does not only hold

regarding imaginary and real part as it does for all realizable systems:

$${\rm Im} \left\{ H(f) \right \} \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, {\rm Re} \left\{ H(f) \right \}\hspace{0.01cm},$$

but additionally also the Hilbert correspondence between the phase and attenuation functions is valid:

$$b(f) \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, a(f)\hspace{0.05cm}.$$

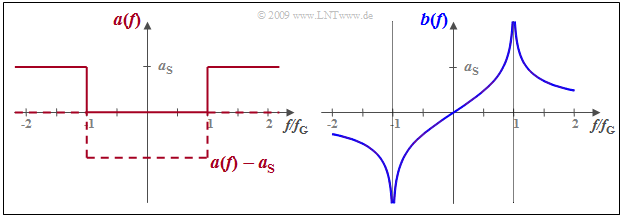
$\text{Example 5:}$ A low-pass filter has the frequency response $H(f) = 1$ ⇒ $a(f) =0$ Np in the »pass band« ⇒ $\vert f \vert < f_{\rm G}$, while for higher frequencies the attenuation function $a(f)$ has the constant value $a_{\rm S}$ $($in Neper$)$.

Attenuation and phase functions of an exemplary minimum-phase low-pass filter

In this »stop band« ⇒ $\vert f \vert > f_{\rm G}$, the frequency response $H(f) = {\rm e}^{–a_{\rm S} }$ is very small but not zero.
If the low-pass filter is to be causal and thus realizable, then the phase function $b(f)$ must be equal to the Hilbert transform of the attenuation $a(f)$ .
Since the Hilbert transform of a constant is zero, the function $a(f) - a_{\rm S}$ can be assumed in the same way.
This function shown dashed in the graph is $($negative$)$ rectangular between $±f_{\rm G}$. According to the $\text{table}$ in the last section the following thus holds:

$$b(f) = {a_{\rm S} }/{\pi} \cdot {\rm ln}\hspace{0.1cm}\left\vert \frac{f+f_{\rm G} }{f-f_{\rm G} }\right \vert \hspace{0.05cm}.$$

$\text{Note:}$ In contrast, any other phase response would result in a non-causal impulse response.

Exercises for the chapter

Exercise 3.1: Causality Considerations

Exercise 3.1Z: Hilbert Transform

References

↑ Marko, H.: Methoden der Systemtheorie. 3. Auflage. Berlin – Heidelberg: Springer, 1994.

[Mar94-1] Marko, H.: Methoden der Systemtheorie. 3. Auflage. Berlin – Heidelberg: Springer, 1994.

[1]