Contents
Complexity of DFT and IDFT
A disadvantage of the direct calculation of the $($generally complex$)$ DFT sequences
- $$\langle \hspace{0.03cm}D(\mu)\hspace{0.03cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.03cm}d(\nu)\hspace{0.03cm} \rangle$$
according to the equations given in chapter »Discrete Fourier Transform» $\rm (DFT)$ is the large computational cost.
We consider as an example the DFT, i.e. the calculation of the $D(\mu)$ coefficients from the $d(\nu)$ coefficients:
- $$N \cdot D(\mu) = \sum_{\nu = 0 }^{N-1} d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} = d(0) \cdot w^{\hspace{0.03cm}0} + d(1) \cdot w^{\hspace{0.03cm}\mu}+ d(2) \cdot w^{\hspace{0.03cm}2\mu}+\hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ d(N-1) \cdot w^{\hspace{0.03cm}(N-1)\cdot \mu}.$$
The computational effort required for this is to be estimated, assuming that the powers of the complex rotation factor $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N}$ already exist in real and imaginary part form in a lookup table. To calculate a single coefficient, one then needs $N-1$ complex multiplications and as many complex additions, observing:
- Each complex addition requires two real additions:
- $$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + R_2) + {\rm j} \cdot (I_1 + I_2)\hspace{0.05cm}.$$
- Each complex multiplication requires four real multiplications and two real additions $($a subtraction is treated as an addition$)$:
- $$(R_1 + {\rm j} \cdot I_1) (R_2 + {\rm j} \cdot I_2) = (R_1 \cdot R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot I_1)\hspace{0.05cm}.$$
- Thus, the following number of real multiplications and the number of real additions are required to calculate all $N$ coefficients in total:
- $$M = 4 \cdot N \cdot (N-1),$$
- $$A = 2 \cdot N \cdot (N-1)+2 \cdot N \cdot (N-1)=M \hspace{0.05cm}.$$
- In today's computers, multiplications and additions/subtractions need about the same computing time. It is sufficient to consider the total number $\mathcal{O} = M + A$ of all operations:
- $$\mathcal{O} = 8 \cdot N \cdot (N-1) \approx 8 \cdot N^2\hspace{0.05cm}.$$
$\text{Conclusion:}$
- For a Discrete Fourier Transform $\rm (DFT)$ with $N = 1000$ one already needs almost eight million arithmetic operations. The same applies to an IDFT.
- With $N =16$ still $1920$ computational operations are required.
- If the parameter $N$ is a power to the base $2$, more computationally efficient algorithms can be applied. The multitude of such methods known from the literature are summarized under the collective term »Fast Fourier Transform« – abbreviated $\text{FFT}$. All these methods are based on the »superposition theorem« of the DFT.
Superposition theorem of the DFT
The graph illustrates the so-called »superposition theorem« of the DFT using the example of» $N = 16$. Shown here is the transition from the time domain to the spectral domain, i.e. the calculation of the spectral domain coefficients from the time domain coefficients: $\langle \hspace{0.03cm}D(\mu)\hspace{0.03cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.03cm} d(\nu) \hspace{0.03cm}\rangle.$
The algorithm described thereby is characterized by the following steps:
- The sequence $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ of length $N$ is divided into two subsequences $\langle \hspace{0.03cm} d_1(\nu)\hspace{0.03cm}\rangle$ and $\langle \hspace{0.03cm} d_2(\nu)\hspace{0.03cm}\rangle$ each of half length $($highlighted in yellow and green respectively in the graphic$)$. With $0 \le \nu \lt N/2$ one thus obtains the sequence elements
- $$d_1(\nu) = d(2\nu), $$
- $$d_2(\nu) = d(2\nu+1) \hspace{0.05cm}.$$
- The initial sequences $\langle \hspace{0.03cm}D_1(\mu )\hspace{0.03cm}\rangle$ and $\langle \hspace{0.03cm}D_2(\mu )\hspace{0.03cm}\rangle$ of the two sub-blocks result from this each by its own DFT, but now only with half length $N/2 = 8$:
- $$\langle \hspace{0.03cm}D_1(\mu) \hspace{0.03cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.03cm}d_1(\nu) \hspace{0.03cm}\rangle , $$
- $$ \langle \hspace{0.03cm}D_2(\mu)\hspace{0.03cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.03cm}d_2(\nu) \hspace{0.03cm}\rangle \hspace{0.05cm}.$$
- The initial values $\langle \hspace{0.03cm} D_2(\mu )\hspace{0.03cm}\rangle$ of the lower (green) DFT $($with $0 \le \mu \lt N/2)$ are then changed in the block outlined in red by complex rotation factors with respect to phase:
- $$D_2(\mu) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}, \hspace{0.2cm}{\rm with}\hspace{0.1cm}w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N} \hspace{0.05cm}.$$
- Each single »butterfly« in the blue bordered block $($in the middle of the graph$)$ yields two elements of the searched sequence by addition or subtraction. With $0 \le \mu \lt N/2$ applies:
- $$D(\mu) = {1}/{2}\cdot \big[D_1(\mu) + D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big],$$
- $$D(\mu +{N}/{2}) = {1}/{2}\cdot \big[D_1(\mu) - D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big]\hspace{0.05cm}.$$
This first application of the superposition theorem thus roughly halves the computational effort.
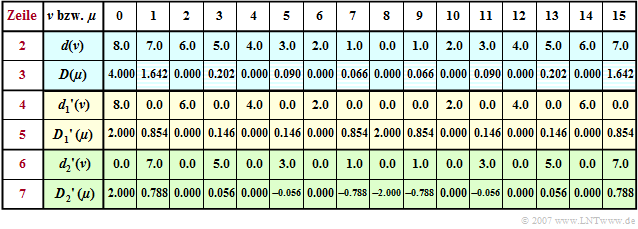
$\text{Example 1:}$ Let the DFT coefficients $d(\nu)$ for the description of the time course be "triangular" according to line 2 of the following table. Note here the periodic continuation of the DFT, so that the linear increase for $t \lt 0$ is given by the coefficients $d(8), \hspace{0.05cm}\text{ ...} \hspace{0.05cm}, d(15)$.
Applying the DFT algorithm with $N = 16$ one obtains the spectral coefficients $D(\mu )$ given in line 3 which would be equal $D(\mu ) = 4 \cdot \text{sinc}^2(\mu/2)$ if the aliasing error were neglected. We can see that the aliasing error only affects the odd coefficients $($shaded boxes$)$. For example, $D(1) = 16/ \pi^2 \approx 1.621\neq 1.642$ should be.
If we split the total sequence $\langle \hspace{0.03cm}d(\nu)\hspace{0.03cm}\rangle$ into two subsequences such that the first subsequence $\langle \hspace{0.03cm}{d_1}'(\nu)\hspace{0.03cm}\rangle$ ⇒ yellow marked has only even coefficients $(\nu = 0, 2, \hspace{0.03cm}\text{ ...} \hspace{0.1cm}, N–2)$ and the second subsequence $\langle \hspace{0.03cm}{d_2}'(\nu)\hspace{0.03cm}\rangle$ ⇒ green marked contains only odd coefficients $(\nu = 1, 3, \hspace{0.03cm}\text{ ...} \hspace{0.1cm} , N-1)$ and all others are set to zero. The corresponding sequences in the spectral domain are obtained:
- $$ \langle \hspace{0.03cm}{D_1}'(\mu)\hspace{0.03cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.03cm} {d_1}'(\nu) \hspace{0.03cm}\rangle , $$
- $$ \langle \hspace{0.03cm}{D_2}'(\mu) \hspace{0.03cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle\hspace{0.03cm} {d_2}'(\nu) \rangle \hspace{0.03cm}\hspace{0.05cm}.$$
In the yellow or green lines $4\hspace{0.05cm}\text{ ...} \hspace{0.05cm}7$ you can see:
- Because of $d(\nu) = {d_1}'(\nu) + {d_2}'(\nu)$ also holds
- $$D(\mu ) = {D_1}'(\mu ) + {D_2}'(\mu ).$$
- This can be justified, for example, with the »Addition Theorem of Linear Systems«.
- The period of the sequence $\langle \hspace{0.03cm}{D_1}'(\mu )\hspace{0.03cm}\rangle$ due to the zeroing of every second time coefficient is now $N/2$ unlike the period $N$ of the sequence $\langle \hspace{0.03cm} D(\mu )\hspace{0.03cm}\rangle$:
- $${D_1}'(\mu + {N}/{2}) ={D_1}'(\mu)\hspace{0.05cm}.$$
- The sequence $\langle \hspace{0.03cm} {D_2}'(\mu )\hspace{0.03cm}\rangle$ additionally contains a phase factor $($shift by one sample$)$ which causes a sign change of two coefficients separated by $N/2$:
- $${D_2}'(\mu + {N}/{2}) = - {D_2}'(\mu)\hspace{0.05cm}.$$
- The calculation of $\langle \hspace{0.03cm}{D_1}'(\mu )\hspace{0.03cm}\rangle$ and $\langle \hspace{0.03cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ is, however, in each case as time-consuming as the determination of $\langle \hspace{0.03cm}D(\mu )\hspace{0.03cm}\rangle$, since $\langle \hspace{0.03cm}{d_1}'(\nu)\hspace{0.03cm}\rangle$ and $\langle \hspace{0.03cm}{d_2}'(\nu)\hspace{0.03cm}\rangle$ also consist of $N$ elements, even if half of them are zeros.
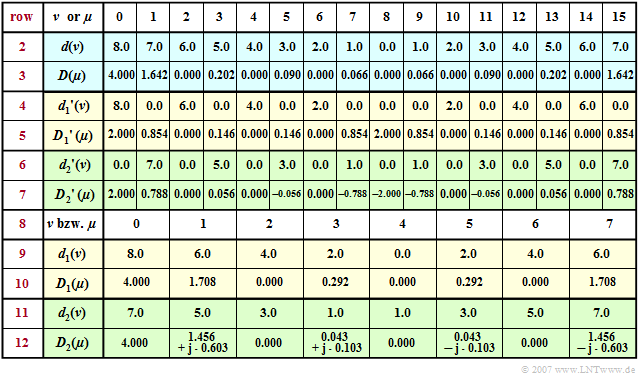
$\text{Example 2:}$ To continue the first example, the previous table is now extended by the rows $8$ to $12$ .
Omitting the coefficients ${d_1}'(\nu) = 0$ with odd indices and ${d_2}'(\nu) = 0$ with even indices, we arrive at the subsequences $\langle \hspace{0.03cm}d_1(\nu)\hspace{0.03cm}\rangle$ and $\langle \hspace{0.03cm}d_2(\nu)\hspace{0.03cm}\rangle$ corresponding to lines $9$ and $11$.
You can see:
- The time sequences $\langle \hspace{0.03cm}{d_1}(\nu )\hspace{0.03cm}\rangle$ and $\langle \hspace{0.03cm}{d_2}(\nu )\hspace{0.03cm}\rangle$ exhibit as well as the corresponding spectral sequences $\langle \hspace{0.03cm}{D_1}(\mu )\hspace{0.03cm}\rangle$ and $\langle \hspace{0.03cm}{D_2}(\mu )\hspace{0.03cm}\rangle$ only have the dimension $(N/2)$.
- A comparison of the lines $5$, $7$, $10$ and $12$ shows the following relationship for $0 \le \mu \lt N/2$ :
- $${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu)\hspace{0.05cm},$$
- $$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu)\cdot w^{\hspace{0.04cm}\mu}\hspace{0.05cm}.$$
- Correspondingly, for $N/2 \le \mu \lt N$:
- $${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu - {N}/{2})\hspace{0.05cm},$$
- $$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu {-} {N}/{2})\cdot w^{\hspace{0.04cm}\mu}$$
- $$ \Rightarrow \hspace{0.3cm}{D_2}'(\mu) = { - } {1}/{2}\cdot {D_2}(\mu-N/2)\cdot w^{\hspace{0.04cm}\mu {-} N/2}\hspace{0.05cm}.$$
- For example, with $N = 16$ ⇒ $w = {\rm e}^{ - {\rm j}\hspace{0.04cm} \cdot \hspace{0.04cm}\pi/8}$ for the indices $\mu = 1$ respectively $\mu = 9$:
- $${D_1}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} {D_2}'(1) ={1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/8} = 0.788$$
- $$\Rightarrow D(1) = {D_1}'(1)+ {D_2}'(1)= 1.642 \hspace{0.05cm}.$$
- $${D_9}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} {D_2}'(9) = - {1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/8} = - 0.788$$
- $$\Rightarrow D(9) = {D_1}'(9)+ {D_2}'(9)= 0.066 \hspace{0.05cm}.$$
$\text{Conclusion:}$
- This first application of the superposition theorem almost halves the computational effort.
- Instead of $\mathcal{O}= 1920$ one only needs $\mathcal{O} = 2 - 448 + 8 \cdot (4+2) + 16 \cdot 2 = 976$ real operations.
- The first summand accounts for the two DFT calculations with $N/2 = 8$.
- The remainder is needed for the eight complex multiplications and the $16$ complex additions and subtractions, respectively.
Radix-2 algorithm according to Cooley and Tukey
Like other FFT algorithms, the method [CT65][1] from »$\text{James W. Cooley}$« and »$\text{John W. Tukey}$« is based on the superposition theorem of the DFT. It only works if the number of interpolation points is a power of two.
The diagram illustrates the algorithm for $N = 8$, again showing the transformation from the time to the frequency domain.
- Before the FFT algorithm, the input values $d(0), \hspace{0.05cm}\text{...} \hspace{0.1cm}, d( N - 1)$ have to be reordered in the grey block »Bit Reversal Operation«.
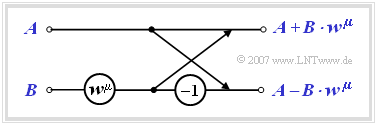
- The computation is done in $\text{log}_2 N = 3$ stages, where in each stage $N/2 = 4$ equal computations are performed with different $\mu$–values as exponent of the complex rotation factor. Such a basic operation is called »butterfly«.
- Each butterfly calculates from two $($generally complex$)$ input variables $A$ and $B$ the two output variables $A + B \cdot w^{\mu}$ and $A - B \cdot w^{\mu}$ according to the following sketch.
$\text{Conclusion:}$ The complex spectral coefficients $D(0), \hspace{0.05cm}\text{...} \hspace{0.1cm}, D( N - 1)$ are obtained at the output of the last stage after division by $N$.
- As shown in $\text{Exercise 5.5Z}$, this results in a much shorter computation time compared to the DFT, for example for $N = 1024$ by more than a factor $150$.
- The inverse DFT for calculating the time coefficients from the spectral coefficients is done with the same algorithm and only slight modifications.
$\text{Example 3:}$ Finally, the C program $\text{fft(N, Re, Im)}$ according to the Radix-2 algorithm described above is given:
- The two float arrays »Re« and »Im» contain the $N$ real and imaginary parts of the complex time coefficients $d(0)$, ... , $d( N - 1)$.
- In the same fields »Re« and »Im» the complex coefficients $D(0)$, ... , $D( N - 1)$ are returned to the main program.
- Due to the »in-place programming«, $N$ complex storage elements are thus sufficient for this algorithm but only if the input values are reordered at the beginning.
- This is done by the program »bit-reversal«, where the contents of ${\rm Re}( \nu)$ and ${\rm Im}( \nu)$ are entered into the elements ${\rm Re}( \kappa)$ and ${\rm Im}( \kappa)$. $\text{Example 4}$ illustrates this procedure.
$\text{Example 4: Bit-reversal operation}$
- The new index $\kappa$ is obtained by writing the index $\nu$ as a dual number and then representing the $\text{log}_2 \hspace{0.05cm} N$ bits in reverse order.
- For example, $\nu = 3$ becomes the new index $\kappa = 6$.
Exercises for the chapter
Exercise 5.5: Fast Fourier Transform
Exercise 5.5Z: Complexity of the FFT
References
- ↑ Cooley, J.W.; Tukey, J.W.: An Algorithm for the Machine Calculation of Complex Fourier Series.
In: Mathematics of Computation, Vol. 19, No. 90. (Apr., 1965), pp. 297-301.