Difference between revisions of "Theory of Stochastic Signals/Auto-Correlation Function"
| Line 18: | Line 18: | ||
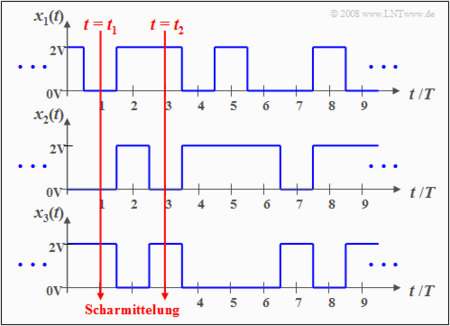
{{Beispiel}}''':''' Die Grafik zeigt drei unterschiedliche Mustersignale mit folgenden Eigenschaften: | {{Beispiel}}''':''' Die Grafik zeigt drei unterschiedliche Mustersignale mit folgenden Eigenschaften: | ||
| − | [[File:Sto_T_4_4_S1.png| | + | |
| + | [[File:Sto_T_4_4_S1.png|450px|right| Zur Definition eines Zufallsprozesses]] | ||
*Der hier vorliegende Zufallsprozess $\{x_i(t)\}$ besteht aus einem Ensemble rechteckförmiger Musterfunktionen, die jeweils wie folgt beschrieben werden können: | *Der hier vorliegende Zufallsprozess $\{x_i(t)\}$ besteht aus einem Ensemble rechteckförmiger Musterfunktionen, die jeweils wie folgt beschrieben werden können: | ||
:$$x_i(t)=\sum^{+\infty}_{\nu=-\infty} (a_\nu)_i\cdot g(t-\nu \cdot T ).$$ | :$$x_i(t)=\sum^{+\infty}_{\nu=-\infty} (a_\nu)_i\cdot g(t-\nu \cdot T ).$$ | ||
| Line 27: | Line 28: | ||
==Stationäre Zufallsprozesse== | ==Stationäre Zufallsprozesse== | ||
| − | Definiert man den Momentanwert aller Musterfunktionen $x_i(t)$ zu einem festen Zeitpunkt $t = t_1$ als eine neue Zufallsgröße $x_1 = \{ | + | [[File:Sto_T_4_4_S2.png|450px |right|450px| Zur Definition stationärer Zufallsprozesse]] |
| + | Definiert man den Momentanwert aller Musterfunktionen $x_i(t)$ zu einem festen Zeitpunkt $t = t_1$ als eine neue Zufallsgröße $x_1 = \{ x_i(t_1)\}$, so lassen sich deren statistische Eigenschaften nach den Aussagen | ||
| + | *des zweiten Kapitels „Diskrete Zufallsgrößen” und | ||
| + | *des dritten Kapitels „Kontinuierliche Zufallsgrößen” | ||
| − | + | in diesem Buch beschreiben. | |
| + | In gleicher Weise erhalten wir für den Betrachtungszeitpunkt $t = t_2$ die Zufallsgröße $x_2 = \{ x_i(t_2)\}$. | ||
| − | + | ''Hinweis:'' Beachten Sie bitte, dass | |
| + | *$x_1(t)$ und $x_2(t)$ Musterfunktionen des Zufallsprozesses $\{x_i(t)\}$ sind, | ||
| + | *während die Zufallsgrößen $x_1$ und $x_2$ den Prozess zu den Zeiten $t_1$ und $t_2$ charakterisieren. | ||
Die Berechnung der statistischen Kenngrößen muss durch Scharmittelung über alle möglichen Musterfunktionen erfolgen (Mittelung über die Laufvariable $i$, also über alle Realisierungen). | Die Berechnung der statistischen Kenngrößen muss durch Scharmittelung über alle möglichen Musterfunktionen erfolgen (Mittelung über die Laufvariable $i$, also über alle Realisierungen). | ||
| − | {{Definition}} | + | {{Definition}}''':''' Bei einem '''stationären Zufallsprozess''' $\{x_i(t)\}$ sind alle statistischen Kenngrößen (Mittelwert, Streuung, Momente höherer Ordnung, Auftrittswahrscheinlichkeiten, etc.) der Zufallsgrößen $x_1$ und $x_2$ gleich. Auch zu jedem anderen Zeitpunkt ergeben sich genau gleiche Werte. |
| − | Bei einem stationären Zufallsprozess { | ||
{{end}} | {{end}} | ||
| − | Die Umkehrung lautet: Man bezeichnet einen Zufallsprozess { | + | Die Umkehrung lautet: Man bezeichnet einen Zufallsprozess $\{x_i(t)\}$ als ''nichtstationär,'' wenn er zu verschiedenen Zeitpunkten unterschiedliche statistische Eigenschaften aufweist. |
| − | |||
| − | |||
| − | |||
| − | Eine vergleichbare Messreihe am 50. Breitengrad würde aufgrund der jahreszeitlichen Schwankungen auf einen ''nichtstationären Prozess'' hinweisen mit deutlichen Unterschieden hinsichtlich Mittelwert und Varianz der Mittagstemperatur zwischen Januar und Juli. | + | {{Box}} |
| + | '''Beispiele:''' | ||
| + | *Eine große Anzahl von Mess-Stationen am Äquator ermitteln täglich um 12 Uhr Ortszeit die Temperatur. Mittelt man über all diese Messwerte, so kann man den Einfluss lokaler Indikatoren (z. B. Golfstrom) eliminieren. Trägt man die Mittelwerte (Scharmittelung) über der Zeit auf, so wird sich nahezu eine Konstante ergeben, und man kann von einem ''stationären Prozess'' sprechen. | ||
| + | *Eine vergleichbare Messreihe am 50. Breitengrad würde aufgrund der jahreszeitlichen Schwankungen auf einen ''nichtstationären Prozess'' hinweisen mit deutlichen Unterschieden hinsichtlich Mittelwert und Varianz der Mittagstemperatur zwischen Januar und Juli. | ||
{{end}} | {{end}} | ||
==Ergodische Zufallsprozesse== | ==Ergodische Zufallsprozesse== | ||
| − | Eine wichtige Unterklasse der stationären Zufallsprozesse sind die so genannten ergodischen Prozesse mit folgenden Eigenschaften: | + | Eine wichtige Unterklasse der stationären Zufallsprozesse sind die so genannten '''ergodischen Prozesse''' mit folgenden Eigenschaften: |
| − | *Bei einem ergodischen Prozess { | + | [[File:Sto_T_4_4_S3.png|450px |right|450px| Zur Definition ergodischer Zufallsprozesse]] |
| + | *Bei einem ergodischen Prozess $\{x_i(t)\}$ ist jede einzelne Musterfunktion $x_i(t)$ repräsentativ für das gesamte Ensemble. | ||
*Alle statistischen Beschreibungsgrößen eines ergodischen Prozesses kann man aus einer einzigen Musterfunktion durch Zeitmittelung (bezüglich der Laufvariablen $ν$) gewinnen. | *Alle statistischen Beschreibungsgrößen eines ergodischen Prozesses kann man aus einer einzigen Musterfunktion durch Zeitmittelung (bezüglich der Laufvariablen $ν$) gewinnen. | ||
*Das bedeutet auch: Bei Ergodizität stimmen die Zeitmittelwerte einer jeden Musterfunktion mit den entsprechenden Scharmittelwerten zu beliebigen Zeitpunkten überein. | *Das bedeutet auch: Bei Ergodizität stimmen die Zeitmittelwerte einer jeden Musterfunktion mit den entsprechenden Scharmittelwerten zu beliebigen Zeitpunkten überein. | ||
*Beispielsweise gilt bei Ergodizität für das Moment $k$-ter Ordnung: | *Beispielsweise gilt bei Ergodizität für das Moment $k$-ter Ordnung: | ||
| − | $$m_k=\overline{x^k(t)}={\rm E}[x^k].$$ | + | :$$m_k=\overline{x^k(t)}={\rm E}[x^k].$$ |
| − | + | :Die überstreichende Linie kennzeichnet hierbei den Zeitmittelwert, während der Scharmittelwert durch Erwartungswertswertbildung $\rm E[ ... ]$ zu ermitteln ist, wie in [[Stochastische_Signaltheorie/Momente_einer_diskreten_Zufallsgröße|Momente einer diskreten Zufallsgröße]] beschrieben. | |
| − | |||
| − | Die überstreichende Linie kennzeichnet hierbei den Zeitmittelwert, während der Scharmittelwert durch Erwartungswertswertbildung E[ ... ] zu ermitteln ist, wie in [[Stochastische_Signaltheorie/Momente_einer_diskreten_Zufallsgröße| | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ''Anmerkung:'' Die Ergodizität lässt sich aus einer endlichen Anzahl von Musterfunktionen und endlichen Signalausschnitten nicht nachweisen. Allerdings wird in den meisten Anwendungen zwar hypothetisch – aber trotzdem durchaus berechtigt – von Ergodizität ausgegangen. Anhand der gefundenen Ergebnisse muss anschließend die Plausibilität dieser '''Ergodizitätshypothese''' überprüft werden. | |
==Allgemeingültige Beschreibung von Zufallsprozessen== | ==Allgemeingültige Beschreibung von Zufallsprozessen== | ||
| − | Ist der zu analysierende Zufallsprozess { | + | Ist der zu analysierende Zufallsprozess $\{x_i(t)\}$ nicht stationär und damit mit Sicherheit auch nicht ergodisch, so müssen die Momente stets als Scharmittelwerte bestimmt werden. Im Allgemeinen sind diese zeitabhängig: |
| − | $$m_k(t_1) \ne m_k(t_2).$$ | + | :$$m_k(t_1) \ne m_k(t_2).$$ |
| − | Da durch die Momente aber auch die [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Charakteristische_Funktion|charakteristische Funktion]] (Fourierrücktransformierte der WDF) | + | Da durch die Momente aber auch die [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Charakteristische_Funktion|'''charakteristische Funktion''']] (Fourierrücktransformierte der WDF) |
| − | $$ C_x(\Omega) ={\rm\sum^{\infty}_{{\it k}=0}}\frac{m_k}{k!}\cdot \Omega^{k}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,f_{ | + | $$ C_x(\Omega) ={\rm\sum^{\infty}_{{\it k}=0}}\frac{m_k}{k!}\cdot \Omega^{k}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,f_{x}(x)$$ |
| − | festliegt, ist die Wahrscheinlichkeitsdichtefunktion $f_{ | + | festliegt, ist die Wahrscheinlichkeitsdichtefunktion $f_{x}(x)$ ebenfalls zeitabhängig. |
| − | Sollen | + | Sollen nicht nur die Amplitudenverteilungen zu verschiedenen Zeitpunkten $t_1, t_2$, ... ermittelt werden, sondern auch die statistischen Bindungen zwischen den Signalwerten zu diesen Zeiten, so muss man auf die '''zweidimensionale Verbundwahrscheinlichkeitsdichtefunktion''' übergehen. |
Betrachtet man beispielsweise die beiden Zeitpunkte $t_1$ und $t_2$, so ist folgendes zu vermerken: | Betrachtet man beispielsweise die beiden Zeitpunkte $t_1$ und $t_2$, so ist folgendes zu vermerken: | ||
| − | *Die 2D-WDF ergibt sich entsprechend den Angaben | + | *Die 2D-WDF ergibt sich entsprechend den Angaben auf der Seite [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen#Eigenschaften_und_Beispiele|Eigenschaften und Beispiele zweidimensionaler Zufallsgrößen]] mit $x = x(t_1)$ und $y = x(t_2)$. Es ist offensichtlich, dass bereits die Ermittlung dieser Größe sehr aufwändig ist. |
*Berücksichtigt man weiter, dass zur Erfassung aller statistischen Bindungen innerhalb des Zufallsprozesses eigentlich die $n$-dimensionale Verbundwahrscheinlichkeitsdichtefunktion (VWDF) herangezogen werden müsste, wobei möglichst noch der Grenzwert $n → ∞$ zu bilden ist, so erkennt man die Schwierigkeiten für die Lösung praktischer Probleme. | *Berücksichtigt man weiter, dass zur Erfassung aller statistischen Bindungen innerhalb des Zufallsprozesses eigentlich die $n$-dimensionale Verbundwahrscheinlichkeitsdichtefunktion (VWDF) herangezogen werden müsste, wobei möglichst noch der Grenzwert $n → ∞$ zu bilden ist, so erkennt man die Schwierigkeiten für die Lösung praktischer Probleme. | ||
*Aus diesen Gründen geht man zur Beschreibung der statistischen Bindungen eines Zufallsprozesses auf die Autokorrelationsfunktion über, die nachfolgend definiert wird. | *Aus diesen Gründen geht man zur Beschreibung der statistischen Bindungen eines Zufallsprozesses auf die Autokorrelationsfunktion über, die nachfolgend definiert wird. | ||
==Allgemeine Definition der Autokorrelationsfunktion== | ==Allgemeine Definition der Autokorrelationsfunktion== | ||
| − | {{Definition}} | + | |
| − | Die Autokorrelationsfunktion (AKF) eines beliebigen Zufallsprozesses { $x_i(t)$} ist gleich dem Erwartungswert des Produkts der Signalwerte zu zwei Zeitpunkten $t_1$ und $t_2$: | + | {{Definition}}''':''' Die '''Autokorrelationsfunktion''' (AKF) eines beliebigen Zufallsprozesses { $x_i(t)$} ist gleich dem Erwartungswert des Produkts der Signalwerte zu zwei Zeitpunkten $t_1$ und $t_2$: |
| − | $$\varphi_x(t_1,t_2)={\rm E}[x(t_{\rm 1})\cdot x(t_{\rm 2})].$$ | + | :$$\varphi_x(t_1,t_2)={\rm E}[x(t_{\rm 1})\cdot x(t_{\rm 2})].$$ |
Diese Definition gilt unabhängig davon, ob der Zufallsprozess ergodisch oder nichtergodisch ist, und sie gilt auch für nichtstationäre Prozesse. | Diese Definition gilt unabhängig davon, ob der Zufallsprozess ergodisch oder nichtergodisch ist, und sie gilt auch für nichtstationäre Prozesse. | ||
{{end}} | {{end}} | ||
Revision as of 16:51, 23 March 2017
Contents
- 1 Zufallsprozesse
- 2 Stationäre Zufallsprozesse
- 3 Ergodische Zufallsprozesse
- 4 Allgemeingültige Beschreibung von Zufallsprozessen
- 5 Allgemeine Definition der Autokorrelationsfunktion
- 6 Autokorrelationsfunktion bei ergodischen Prozessen
- 7 Eigenschaften der Autokorrelationsfunktion
- 8 Interpretation der Autokorrelationsfunktion
- 9 Numerische AKF-Ermittlung
- 10 Genauigkeit der numerischen AKF-Berechnung
Zufallsprozesse
Ein wichtiger Begriff der stochastischen Signaltheorie ist der Zufallsprozess. Nachfolgend sind einige Charakteristika eines solchen stochastischen Prozesses – diese Bezeichnungen werden sowohl in der Literatur als auch in unserem Tutorial synonym verwendet – zusammengestellt:
- Unter einem Zufallsprozess $\{x_i(t)\}$ verstehen wir ein mathematisches Modell für ein Ensemble von (vielen) Zufallssignalen, die sich zwar im Detail durchaus voneinander unterscheiden können, trotzdem aber gewisse gemeinsame Eigenschaften aufweisen.
- Zur Beschreibung eines Zufallsprozesses $\{x_i(t)\}$ gehen wir von der Vorstellung aus, dass beliebig viele, in ihren physikalischen und statistischen Eigenschaften völlig gleiche Zufallsgeneratoren vorhanden sind, von denen jeder ein Zufallssignal $x_i(t)$ liefert.
- Jeder Zufallsgenerator gibt trotz gleicher physikalischer Realisierung ein anderes Zeitsignal $x_i(t)$ ab, das für alle Zeiten von $–∞$ bis $+∞$ existiert. Man bezeichnet dieses spezifische Zufallssignal als das $i$-te Mustersignal.
- Jeder Zufallsprozess beinhaltet mindestens eine stochastische Komponente – zum Beispiel die Amplitude, Frequenz oder Phase eines Nachrichtensignals – und kann daher von einem Beobachter nicht exakt vorausgesagt werden.
- Der Zufallsprozess unterscheidet sich von den sonst in der Wahrscheinlichkeitsrechnung bzw. der Statistik üblichen Zufallsexperimenten dadurch, dass das Ergebnis kein Ereignis ist, sondern ein Funktionsverlauf (Zeitsignal).
- Betrachtet man den Zufallsprozess $\{x_i(t)\}$ zu einem festen Zeitpunkt, so gelangt man wieder zu dem einfacheren Modell von Kapitel Vom Zufallsexperiment zur Zufallsgröße, nach dem das Versuchsergebnis ein Ereignis ist, das einer Zufallsgröße zugeordnet werden kann.
Diese Aussagen werden nun am Beispiel eines binären Zufallsgenerators verdeutlicht, der – zumindest gedanklich – beliebig oft realisiert werden kann.
- Der hier vorliegende Zufallsprozess $\{x_i(t)\}$ besteht aus einem Ensemble rechteckförmiger Musterfunktionen, die jeweils wie folgt beschrieben werden können:
- $$x_i(t)=\sum^{+\infty}_{\nu=-\infty} (a_\nu)_i\cdot g(t-\nu \cdot T ).$$
- Der Grundimpuls $g(t)$ besitzt im Bereich von $–T/2$ bis $+T/2$ den Wert $2\hspace{0.03cm}\rm V$; außerhalb ist er $0$. Unter einem Impuls verstehen wir gemäß der Definition im Kapitel Klassifizierung von Signalen im Buch „Signaldarstellung” ein sowohl deterministisches als auch energiebegrenztes Signal.
- Die Statistik des hier betrachteten Zufallsprozesses ist somit allein auf die dimensionslosen Amplitudenkoeffizienten $(a_ν)_i ∈ \{0, 1\}$ zurückzuführen, die bei der $i$-ten Musterfunktion mit dem Zeitindex $ν$ versehen sind.
- Trotz der im Detail unterschiedlichen Signalverläufe weisen die skizzierten Mustersignale $x_1(t)$, $x_2(t)$, $x_3(t)$ und auch alle weiteren Mustersignale $x_4(t)$, $x_5(t)$, $x_6(t)$, ... gewisse Gemeinsamkeiten auf, die nachfolgend herausgearbeitet werden sollen.
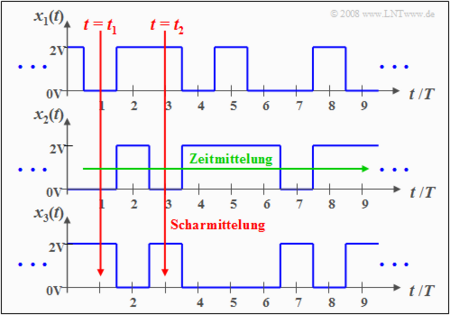
Stationäre Zufallsprozesse
Definiert man den Momentanwert aller Musterfunktionen $x_i(t)$ zu einem festen Zeitpunkt $t = t_1$ als eine neue Zufallsgröße $x_1 = \{ x_i(t_1)\}$, so lassen sich deren statistische Eigenschaften nach den Aussagen
- des zweiten Kapitels „Diskrete Zufallsgrößen” und
- des dritten Kapitels „Kontinuierliche Zufallsgrößen”
in diesem Buch beschreiben.
In gleicher Weise erhalten wir für den Betrachtungszeitpunkt $t = t_2$ die Zufallsgröße $x_2 = \{ x_i(t_2)\}$.
Hinweis: Beachten Sie bitte, dass
- $x_1(t)$ und $x_2(t)$ Musterfunktionen des Zufallsprozesses $\{x_i(t)\}$ sind,
- während die Zufallsgrößen $x_1$ und $x_2$ den Prozess zu den Zeiten $t_1$ und $t_2$ charakterisieren.
Die Berechnung der statistischen Kenngrößen muss durch Scharmittelung über alle möglichen Musterfunktionen erfolgen (Mittelung über die Laufvariable $i$, also über alle Realisierungen).
Die Umkehrung lautet: Man bezeichnet einen Zufallsprozess $\{x_i(t)\}$ als nichtstationär, wenn er zu verschiedenen Zeitpunkten unterschiedliche statistische Eigenschaften aufweist.
Beispiele:
- Eine große Anzahl von Mess-Stationen am Äquator ermitteln täglich um 12 Uhr Ortszeit die Temperatur. Mittelt man über all diese Messwerte, so kann man den Einfluss lokaler Indikatoren (z. B. Golfstrom) eliminieren. Trägt man die Mittelwerte (Scharmittelung) über der Zeit auf, so wird sich nahezu eine Konstante ergeben, und man kann von einem stationären Prozess sprechen.
- Eine vergleichbare Messreihe am 50. Breitengrad würde aufgrund der jahreszeitlichen Schwankungen auf einen nichtstationären Prozess hinweisen mit deutlichen Unterschieden hinsichtlich Mittelwert und Varianz der Mittagstemperatur zwischen Januar und Juli.
Ergodische Zufallsprozesse
Eine wichtige Unterklasse der stationären Zufallsprozesse sind die so genannten ergodischen Prozesse mit folgenden Eigenschaften:
- Bei einem ergodischen Prozess $\{x_i(t)\}$ ist jede einzelne Musterfunktion $x_i(t)$ repräsentativ für das gesamte Ensemble.
- Alle statistischen Beschreibungsgrößen eines ergodischen Prozesses kann man aus einer einzigen Musterfunktion durch Zeitmittelung (bezüglich der Laufvariablen $ν$) gewinnen.
- Das bedeutet auch: Bei Ergodizität stimmen die Zeitmittelwerte einer jeden Musterfunktion mit den entsprechenden Scharmittelwerten zu beliebigen Zeitpunkten überein.
- Beispielsweise gilt bei Ergodizität für das Moment $k$-ter Ordnung:
- $$m_k=\overline{x^k(t)}={\rm E}[x^k].$$
- Die überstreichende Linie kennzeichnet hierbei den Zeitmittelwert, während der Scharmittelwert durch Erwartungswertswertbildung $\rm E[ ... ]$ zu ermitteln ist, wie in Momente einer diskreten Zufallsgröße beschrieben.
Anmerkung: Die Ergodizität lässt sich aus einer endlichen Anzahl von Musterfunktionen und endlichen Signalausschnitten nicht nachweisen. Allerdings wird in den meisten Anwendungen zwar hypothetisch – aber trotzdem durchaus berechtigt – von Ergodizität ausgegangen. Anhand der gefundenen Ergebnisse muss anschließend die Plausibilität dieser Ergodizitätshypothese überprüft werden.
Allgemeingültige Beschreibung von Zufallsprozessen
Ist der zu analysierende Zufallsprozess $\{x_i(t)\}$ nicht stationär und damit mit Sicherheit auch nicht ergodisch, so müssen die Momente stets als Scharmittelwerte bestimmt werden. Im Allgemeinen sind diese zeitabhängig:
- $$m_k(t_1) \ne m_k(t_2).$$
Da durch die Momente aber auch die charakteristische Funktion (Fourierrücktransformierte der WDF) $$ C_x(\Omega) ={\rm\sum^{\infty}_{{\it k}=0}}\frac{m_k}{k!}\cdot \Omega^{k}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,f_{x}(x)$$ festliegt, ist die Wahrscheinlichkeitsdichtefunktion $f_{x}(x)$ ebenfalls zeitabhängig.
Sollen nicht nur die Amplitudenverteilungen zu verschiedenen Zeitpunkten $t_1, t_2$, ... ermittelt werden, sondern auch die statistischen Bindungen zwischen den Signalwerten zu diesen Zeiten, so muss man auf die zweidimensionale Verbundwahrscheinlichkeitsdichtefunktion übergehen.
Betrachtet man beispielsweise die beiden Zeitpunkte $t_1$ und $t_2$, so ist folgendes zu vermerken:
- Die 2D-WDF ergibt sich entsprechend den Angaben auf der Seite Eigenschaften und Beispiele zweidimensionaler Zufallsgrößen mit $x = x(t_1)$ und $y = x(t_2)$. Es ist offensichtlich, dass bereits die Ermittlung dieser Größe sehr aufwändig ist.
- Berücksichtigt man weiter, dass zur Erfassung aller statistischen Bindungen innerhalb des Zufallsprozesses eigentlich die $n$-dimensionale Verbundwahrscheinlichkeitsdichtefunktion (VWDF) herangezogen werden müsste, wobei möglichst noch der Grenzwert $n → ∞$ zu bilden ist, so erkennt man die Schwierigkeiten für die Lösung praktischer Probleme.
- Aus diesen Gründen geht man zur Beschreibung der statistischen Bindungen eines Zufallsprozesses auf die Autokorrelationsfunktion über, die nachfolgend definiert wird.
Allgemeine Definition der Autokorrelationsfunktion
- $$\varphi_x(t_1,t_2)={\rm E}[x(t_{\rm 1})\cdot x(t_{\rm 2})].$$
Diese Definition gilt unabhängig davon, ob der Zufallsprozess ergodisch oder nichtergodisch ist, und sie gilt auch für nichtstationäre Prozesse.
Ein Vergleich mit Kapitel 4.1 zeigt, dass der AKF-Wert $φ_x(t_1, t_2)$ das gemeinsame Moment $m_{11}$ zwischen den beiden Zufallsgrößen $x(t_1)$ und $x(t_2)$ angibt.
Hinweis: Um den Zusammenhang mit der Kreuzkorrelationsfunktion $φ_{xy}$ zwischen den beiden statistischen Größen $x$ und $y$ deutlich zu machen (siehe Kapitel 4.6), wird in mancher Literatur für die AKF auch häufig die Schreibweise $φ_{xx}(t_1, t_2)$ verwendet.
Während für exakte Aussagen hinsichtlich der statistischen Bindungen eines Zufallsprozesses eigentlich die $n$-dimensionale Verbunddichte (mit $n → ∞$) benötigt wird, werden durch den Übergang auf die Autokorrelationsfunktion implizit folgende Vereinfachungen getroffen:
- Anstelle von unendlich vielen Zeitpunkten werden hier nur zwei betrachtet.
- Anstelle aller Momente $m_{kl}$ zu den beiden Zeitpunkten $t_1$ und $t_2$ mit $k, l ∈$ {1, 2, 3, ...} wird hier nur das gemeinsame Moment $m_{11}$ erfasst.
- Das Moment $m_{11}$ gibt ausschließlich die lineare Abhängigkeit (Korrelation) des Prozesses wieder. Alle statistische Bindungen höherer Ordnung werden dagegen nicht berücksichtigt.
- Deshalb sollte bei der Bewertung von Zufallsprozessen mittels AKF stets berücksichtigt werden, dass diese nur sehr beschränkte Aussagen über die statistischen Bindungen erlaubt.
Die obige Definition der Autokorrelationsfunktion gilt allgemein, also auch für nichtstationäre und nichtergodische Prozesse. Ein Beispiel eines nichtstationären Vorgangs ist das Auftreten von Impulsstörungen im Fernsprechnetz, verursacht durch Wählimpulse in benachbarten Leitungen. Bei Digitalsignalübertragung führen solche nichtstationären Störprozesse meist zu Bündelfehlern.
Autokorrelationsfunktion bei ergodischen Prozessen
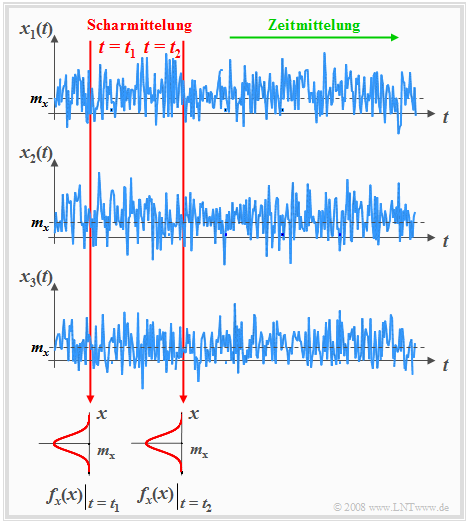
Im Folgenden beschränken wir uns auf stationäre und ergodische Prozesse. Ein solcher Prozess { $x_i(t)$} wird zum Beispiel bei der Untersuchung von Thermischem Rauschen zugrunde gelegt. Dabei wird von der Vorstellung ausgegangen, dass beliebig viele, in ihren physikalischen und statistischen Eigenschaften völlig gleiche Widerstände vorhanden sind, von denen jeder ein anderes Zufallssignal $x_i(t)$ abgibt.
Zu dieser Grafik ist anzumerken:
- Die einzelnen Musterfunktionen $x_i(t)$ können zu allen beliebigen Zeiten alle beliebigen Werte annehmen. Das bedeutet, dass der hier betrachtete Zufallsprozess { $x_i(t)$} sowohl wert– als auch zeitkontinuierlich ist.
- Auch wenn über die tatsächlichen Signalwerte der einzelnen Musterfunktionen aufgrund der Stochastik keine Aussagen getroffen werden können, so sind die Momente und die WDF zu allen Zeitpunkten gleich.
- In obiger Grafik ist aus Gründen einer verallgemeinerten Darstellung auch ein Gleichanteil $m_x$ berücksichtigt, der bei Thermischem Rauschen nicht vorhanden ist.
Von einem stationären Zufallsprozess { $x_i(t)$} spricht man, wenn seine statistischen Eigenschaften invariant gegenüber Zeitverschiebungen sind. Für die Autokorrelationsfunktion (AKF) bedeutet diese Aussage, dass sie nicht mehr eine Funktion der beiden unabhängigen Zeitvariablen $t_1$ und $t_2$ ist, sondern nur noch von der Zeitdifferenz $τ = t_2 – t_1$ abhängt: $$\varphi_x(t_1,t_2)\rightarrow{\varphi_x(\tau)={\rm E}[x(t)\cdot x(t+\tau)]}.$$ Die Scharmittelung kann dabei zu jeder beliebigen Zeit $t$ erfolgen.
Unter der weiteren Annahme eines ergodischen Zufallsprozesses können alle Momente auch durch Zeitmittelung über eine einzige ausgewählte Musterfunktion $x(t)$ ermittelt werden. Diese Zeitmittelwerte stimmen mit den entsprechenden Scharmittelwerten überein.
Damit folgt für die AKF eines ergodischen Prozesses, dessen Mustersignale jeweils von $–∞$ bis $+∞$ reichen $(T_{\rm M}$ bezeichnet die Messdauer): $$\varphi_x(\tau)=\overline{x(t)\cdot x(t+\tau)}=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot x(t+\tau)\,\,{\rm d}t.$$ Die überstreichende Linie kennzeichnet die Zeitmittelung über das unendlich ausgedehnte Zeitintervall.
Bei periodischen Signalen kann man auf den Grenzübergang verzichten, so dass in diesem Sonderfall die Autokorrelationsfunktion mit der Periodendauer $T_0$ auch in folgender Weise geschrieben werden kann:
$$\varphi_x(\tau)=\frac{1}{T_{\rm 0}}\cdot\int^{T_{\rm 0}/2}_{-T_{\rm 0}/2}x(t)\cdot x(t+\tau)\,\,{\rm d}t=\frac{1}{T_{\rm 0}}\cdot\int^{T_{\rm 0}}_{\rm 0}x(t)\cdot x(t+\tau)\,\,{\rm d}t .$$
Wichtig ist dabei nur, dass insgesamt genau über eine Periodendauer $T_0$ (oder Vielfache davon) gemittelt wird. Es ist egal, welcher Zeitausschnitt dabei verwendet wird.
Eigenschaften der Autokorrelationsfunktion
Nachfolgend sind wichtige Eigenschaften der Autokorrelationsfunktion (AKF) zusammengestellt:
- Ist der betrachtete Zufallsprozess reell, so gilt dies auch für seine AKF.
- Die AKF besitzt die Einheit einer Leistung, beispielsweise Watt („W”). Häufig bezieht man diese auf den Einheitswiderstand 1 Ω; in diesem Fall hat $φ_x(τ)$ die Einheit $„\rm V^2”$ bzw. $„\rm A^2”.$
- Die AKF ist immer eine gerade Funktion ⇒ $φ_x(–τ) = φ_x(τ)$. Alle Phasenbeziehungen des Zufallsprozesses gehen in der AKF verloren.
- Die AKF an der Stelle $τ =$ 0 gibt den quadratischen Mittelwert $m_2$ (Moment 2. Ordnung) und damit die gesamte Signalleistung (Gleich– und Wechselanteil) an:
$$\varphi_x(0)= m_2=\overline{ x^2(t)}.$$
- Das AKF–Maximum ist stets bei $τ =$ 0, und es gilt: $|φ_x(τ)| ≤ φ_x(0)$. Bei nichtperiodischen Prozessen ist für $τ ≠$ 0 der Betrag $|φ_x(τ)|$ stets kleiner als die Leistung $φ_x(0)$.
- Bei einem periodischen Zufallsprozess weist die AKF die gleiche Periodendauer $T_0$ wie die einzelnen Mustersignale $x_i(t)$ auf:
$$\varphi_x(\pm{T_0})=\varphi_x(\pm{2\cdot T_0})= \hspace{0.1cm}... \hspace{0.1cm}= \varphi_x(0).$$
- Der Gleichanteil $m_1$ eines nichtperiodischen Signals kann aus dem Grenzwert der AKF für $τ → ∞$ berechnet werden. Hierbei gilt:
$$\lim_{\tau\to\infty}\,\varphi_x(\tau)= m_1^2=[\overline{ x(t)}]^2.$$
- Dagegen schwankt bei Signalen mit periodischen Anteilen der Grenzwert der AKF für $τ → ∞$ um diesen Endwert (Quadrat des Gleichanteils).
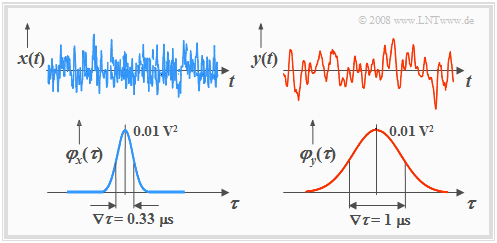
Interpretation der Autokorrelationsfunktion
Das nachfolgende Bild zeigt oben je ein Mustersignal zweier verschiedener Prozesse { $x_i(t)$} und { $y_i(t)$}, unten die zugehörigen Autokorrelationsfunktionen. Der Prozess { $y_i(t)$} weist stärkere innere statistische Bindungen auf als { $x_i(t)$}. Spektral gesehen ist er niederfrequenter.
Anhand dieser Grafiken sind folgende Aussagen möglich:
- Die beiden Mustersignale lassen bereits vermuten, dass beide Prozesse mittelwertfrei sind den gleichen Effektivwert aufweisen.
- Anhand der Autokorrelationsfunktionen werden diese Aussagen bestätigt. Die liearen Mittelwerte $m_x = m_y =$ 0 ergeben sich jeweils aus dem AKF-Grenzwert für $τ → ∞$.
- Wegen $m_x =$ 0 gilt für die Varianz: $σ_x^2 = φ_x(0) = 0.01 \rm V^2$, und der Effektivwert ist somit $σ_x = 0.1 \rm V$. Das Signal $y(t)$ weist die gleiche Varianz und und den gleichen Effektivwert auf.
- Die AKF-Werte fallen um so langsamer ab, je stärker die inneren statistischen Bindungen sind. Während sich das Signal $x(t)$ mit relativ schmaler AKF zeitlich sehr schnell ändert, reichen bei dem niederfrequenteren Signal $y(t)$ die statistischen Bindungen deutlich weiter.
- Das bedeutet aber auch, dass der Signalwert $y(t + τ)$ aus $y(t)$ besser vorhergesagt werden kann als $x(t + τ)$ aus $x(t)$.
- Eine quantitative Kenngröße für die Stärke der statistischen Bindungen ist die äquivalente AKF-Dauer $∇τ$, die sich aus der AKF über das flächengleiche Rechteck ermitteln lässt:
$${ {\rm \nabla} }\tau =\frac{1}{\varphi_x(0)}\cdot\int^{\infty}_{-\infty}\ \varphi_x(\tau)\,\,{\rm d}\tau. \hspace{2cm} \it {Hinweis:} \ {\rm Man \ spricht \ „Nabla–tau”.} $$
- Beim hier betrachteten Prozess (mit gaußähnlicher AKF) ist $∇τ =$ 0.33 μs bzw. $∇τ =$ 1 μs.
- Als ein weiteres Maß für die Stärke der statistischen Bindungen wird in der Literatur häufig die Korrelationsdauer $T_{\rm K}$ verwendet. Diese gibt die Zeitdauer an, bei der die AKF auf die Häfte ihres Maximalwertes abgefallen ist.
Numerische AKF-Ermittlung
Bisher haben wir stets zeitkontinuierliche Signale $x(t)$ betrachtet, die für die Darstellung und Simulation mittels Digitalrechner ungeeignet sind. Hierzu ist eine zeitdiskrete Signaldarstellung $〈x_ν〉$ erforderlich, wie im Kapitel 5.1 von Buch Signaldarstellung dargelegt. Hier eine kurze Zusammenfassung:
Das zeitdiskrete Signal $〈x_ν〉$ ist die Folge der Abtastwerte $x_ν = x(ν · T_{\rm A}).$ Das zeitkontinuierliche Signal $x(t)$ wird durch die Folge $〈x_ν〉$ vollständig beschrieben, wenn das Abtasttheorem erfüllt ist: $$T_{\rm A} \le \frac{1}{\rm 2 \cdot B_x}.$$
$B_x$ bezeichnet hierbei die absolute (einseitige) Bandbreite des Analogsignals $x(t)$. Diese sagt aus, dass die Spektralfunktion $X(f)$ für alle Frequenzen $| f | > B_x$ gleich 0 ist.
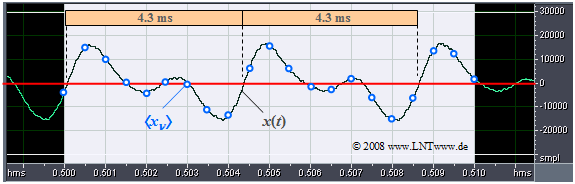
Das Bild zeigt einen Ausschnitt eines Audiosignals der Dauer 10 Millisekunden. Obwohl das gesamte Signal ein breites Spektrum mit der Mittenfrequenz bei etwa 500 Hz besitzt, ist während des betrachteten Zeitintervalls ein (nahezu) periodisches Signal mit Periodendauer $T_0 =$ 4.3 Millisekunden zu erkennen. Daraus ergibt sich die Grundfrequenz zu etwa $f_0 =$ 230 Hz.
Blau eingezeichnet sind die Abtastwerte im Abstand $T_{\rm A} =$ 0.5 ms. Diese Folge $〈x_ν〉$ von Abtastwerten würde die gesamte Information über das Signal $x(t)$ beinhalten, wenn das Analogsignal $x(t)$ auf den Frequenzbereich bis 1 kHz begrenzt wäre. Sind im Signal $x(t)$ höhere Frequenzanteile enthalten, so muss $T_{\rm A}$ entsprechend kleiner gewählt werden.
Da nun die Signalwerte nur zu diskreten Zeitpunkten (bei Vielfachen von $T_{\rm A}$) vorliegen, kann man auch die Autokorrelationsfunktion nur zu ganzzahligen Vielfachen von $T_{\rm A}$ bestimmen. Mit den zeitdiskreten Signalwerten $x_ν = x(ν · T_{\rm A})$ und $x_{ν+k} = x((ν+k) · T_{\rm A})$ sowie der zeitdiskreten AKF $φ_k = φ_x(k · T_{\rm A})$ lässt sich somit die AKF–Berechnung wie folgt dargestellen:
$$\varphi_k = \overline {x_\nu \cdot x_{\nu + k}}.$$
Die überstreichende Linie kennzeichnet hierbei wieder die Zeitmittelung.
Wir stellen uns nun die Aufgabe, die AKF-Stützstellen $φ_0, ... , φ_l$ aus $N$ Abtastwerten $(x_1, .... , x_N)$ zu ermitteln, wobei der Parameter $l$ sehr viel kleiner als $N$ vorausgesetzt wird. Beispielsweise gelte $l =$ 100 und $N =$ 100000.
Die AKF-Berechnungsvorschrift lautet nun (mit 0 ≤ $k$ ≤ $l$): $$\varphi_k = \frac{1}{N- k} \cdot \sum_{\nu = 1}^{N - \lambda} x_{\nu} \cdot x_{\nu + k}.$$ Bringen wir $N – k$ auf die linke Seite, so erhalten wir daraus $l +$ 1 Gleichungen, nämlich: $$k = 0: \hspace{0.4cm}N \cdot \varphi_0 \hspace{1.03cm}=\hspace{0.1cm} x_{\rm 1} \cdot x_{\rm 1} \hspace{0.35cm}+ x_{\rm 2} \cdot x_{\rm 2} \hspace{0.3cm}+ ... \hspace{0.25cm}+x_{\nu} \cdot x_{\nu}\hspace{0.35cm}+ ... \hspace{0.05cm}+x_{N} \cdot x_{N},$$ $$k= 1: \hspace{0.3cm}(N-1) \cdot \varphi_1 \hspace{0.08cm}=\hspace{0.1cm} x_{\rm 1} \cdot x_{\rm 2} \hspace{0.4cm}+ x_{\rm 2} \cdot x_{\rm 3} \hspace{0.3cm}+ ... \hspace{0.18cm}+x_{\nu} \cdot x_{\nu + 1}\hspace{0.01cm}+ ... \hspace{0.08cm}+x_{N-1} \cdot x_{N},$$ $$..................................................$$ $$k \hspace{0.2cm}{\rm allg.:}\hspace{0.31cm}(N - k) \cdot \varphi_k \hspace{0.01cm}=\hspace{0.1cm} x_{\rm 1} \cdot x_{ {\rm 1} + k} \hspace{0.01cm}+ x_{\rm 2} \cdot x_{ {\rm 2}+ k}\hspace{0.1cm} + ... \hspace{0.01cm}+x_{\nu} \cdot x_{\nu+k}\hspace{0.1cm}+ ... \hspace{0.01cm}+x_{N-k} \cdot x_{N},$$ $$..................................................$$ $$k = l: \hspace{0.3cm}(N - l) \cdot \varphi_l \hspace{0.14cm}=\hspace{0.1cm} x_{\rm 1} \cdot x_{ {\rm 1}+l} \hspace{0.09cm}+ x_{\rm 2} \cdot x_{ {\rm 2}+ l} \hspace{0.09cm}+ ... \hspace{0.09cm}+x_{\nu} \cdot x_{\nu+ l} \hspace{0.09cm}+ ... \hspace{0.09cm}+x_{N- l} \cdot x_{N}.$$
Hieraus ergibt sich der folgende Algorithmus:
- Man definiert das Feld AKF[0 : $l$] vom Typ float und belegt alle Elemente mit Nullen vor.
- Bei jedem Schleifendurchlauf (indiziert mit der Variablen $k$) werden die $l$ + 1 Feldelemente AKF[ $k$] jeweils um den Betrag $x_ν · x_{ν+k}$ erhöht.
- Alle $l$ + 1 Feldelemente werden allerdings nur dann bearbeitet, so lange die Laufvariable $k$ nicht größer als $N – l$ ist. Es ist stets zu berücksichtigen, dass $ν + k ≤ N$ gelten muss. Das bedeutet, dass die Mittelung in den unterschiedlichen Feldern AKF[0] ... AKF[ $l$] über eine unterschiedliche Anzahl von Summanden erfolgt.
- Werden am Ende der Berechnung noch die in AKF[ $k$] gespeicherten Werte durch die Anzahl der Summanden $(N – k)$ dividiert, so enthält dieses Feld die gesuchten diskreten AKF-Werte:
$$\varphi_x(k \cdot T_A)= {\rm AKF} \left[k \right].$$
Anmerkung: Bei $l << N$ kann man den Algorithmus vereinfachen, indem die Anzahl der Summanden für alle $k$-Werte gleich gewählt werden:
$$\varphi_k = \frac{1}{N- l} \cdot \sum_{\nu = 1}^{N - l} x_{\nu} \cdot x_{\nu + k}.$$
Genauigkeit der numerischen AKF-Berechnung
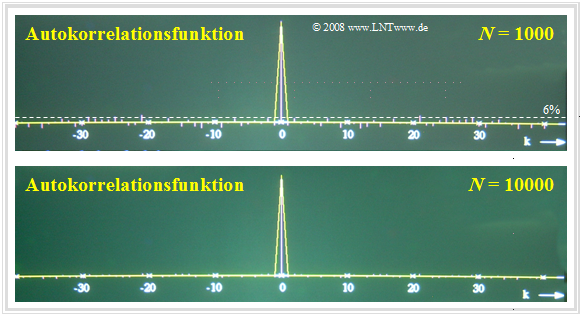
Der entscheidende Parameter für die Qualität der numerischen AKF-Berechnung ist die Anzahl $N$ der berücksichtigten Abtastwerte. Im nachfolgenden oberen Bild sehen Sie das Ergebnis für $N =$ 1000 und darunten für $N =$ 10000 Zufallsgrößen.
Die betrachteten Zufallsgrößen sind hier voneinander statistisch unabhängig. Somit sollten eigentlich alle AKF-Werte mit Ausnahme des Wertes bei $k =$ 0 identisch Null sein. Bei $N =$ 10000 (untere Grafik) beträgt der maximale Fehler nur etwa 1% und ist bei dieser Darstellung fast gar nicht sichtbar. Dagegen wächst der Fehler bei $N =$ 1000 bis auf ±6% an (Markierung beachten).
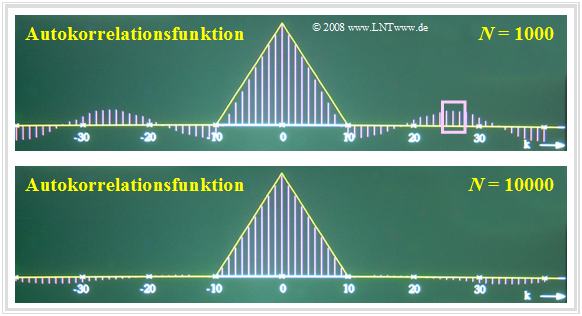
Die Ergebnisse ändern sich, wenn eine Zufallsgröße mit inneren statistischen Bindungen vorliegt. Betrachten wir beispielsweise eine dreieckförmige AKF mit $φ_x(k) ≠$ 0 für $|k|$ ≤ 10, so erkennt man deutlich größere Abweichungen, nämlich Fehler bis zu
- etwa ±15% bei $N =$ 1000,
- etwa ±5% bei $N =$ 10000.
Begründung des schlechteren Ergebnisses:
- Aufgrund der inneren statistischen Bindungen liefern nun nicht mehr alle Abtastwerte die volle Information über den zugrundeliegenden Zufallsprozess.
- Außerdem lassen die Bilder erkennen, dass bei der numerischen AKF-Berechnung einer Zufallsgröße mit statistischen Bindungen auch die Fehler korreliert sind.
- Ist – wie beispielsweise im oberen Bild zu sehen – der AKF-Wert $φ_x({\rm 26})$ fälschlicherweise positiv und groß, so ergeben sich auch die benachbarten AKF-Werte $φ_x({\rm 25})$ und $φ_x({\rm 27})$ als positiv und mit ähnlichen Zahlenwerten. Dieser Bereich ist durch das Rechteck markiert.