Aufgaben:Exercise 4.8: Diamond-shaped Joint PDF

• Return to book

Wir betrachten eine 2D–Zufallsgröße $(x, y)$, deren Komponenten sich jeweils als Linearkombinationen zweier Zufallsgrößen $u$ und $v$ ergeben:

$$x=2u-2v+1,$$

$$y=u+3v.$$

Weiter ist zu beachten:

• Die zwei statistisch unabhängigen Zufallsgrößen $u$ und $v$ sind jeweils gleichverteilt zwischen $0$ und $1$.
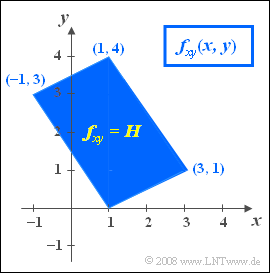
• In der Abbildung sehen Sie die 2D–WDF. Innerhalb des blau eingezeichneten Parallelogramms gilt:   $f_{xy}(x, y) = H = {\rm const.}.$
• Außerhalb des Parallelogramms sind keine Werte möglich:   $f_{xy}(x, y) = 0$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Linearkombinationen von Zufallsgrößen.
• Bezug genommen wird auch auf die Seite Korrelationsgerade.
• Gehen Sie - wenn möglich - von den zwei angegebenen Gleichungen aus und nutzen Sie die Informationen der obigen Skizze vorwiegend nur zur Kontrolle Ihrer Ergebnisse.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Wie groß ist die Höhe $H$ der 2D–WDF innerhalb des Parallelogramms?

$H \ =$

2

Welche Werte von $u$ und $v$ liegen dem Eckpunkt $(-1, 3)$ zugrunde?

$u \ =$

$v \ =$

3

Berechnen Sie den Korrelationskoeffizienten $\rho_{xy}$.

$\rho_{xy}\ =$

4

Wie lautet die Korrelationsgerade $y=K(x)$? Bei welchem Punkt $y_0$ schneidet diese die $y$-Achse?

$y_0\ =$

5

Berechnen Sie die Randwahrscheinlichkeitsdichtefunktion $f_x(x)$. Wie groß ist die Wahrscheinlichkeit, dass die Zufallsgröße $x$ negativ ist.

${\rm Pr}(x < 0)\ =$

6

Berechnen Sie die Randwahrscheinlichkeitsdichtefunktion $f_y(y)$. Wie groß ist die Wahrscheinlichkeit, dass die Zufallsgröße $y >3$ ist?

${\rm Pr}(y > 3)\ =$

Musterlösung

Solution

(1)  Die Fläche des Parallelogramms kann aus zwei gleich großen Dreiecken zusammengesetzt werden. Die Fläche des Dreiecks $(1,0)(1,4)-1,3)$ ergibt 0.5 · 4 · 2 = 4. Die Gesamtfläche ist doppelt so groß:   $F = 8$. Da das WDF-Volumen stets $1$ ist, gilt $H= 1/F\hspace{0.15cm}\underline{ = 0.125}$.

(2)  Der minimale Wert von $x$ ergibt sich für $\underline{ u=0}$ und $\underline{ v=1}$. Daraus folgen aus obigen Gleichungen die Ergebnisse $x= -1$ und $y= +3$.

(3)  Die im Theorieteil angegebene Gleichung gilt allgemein, d. h. für jede beliebige WDF der beiden statistisch unabhängigen Größen $u$ und $v$, so lange diese gleiche Streuungen aufweisen $(\sigma_u = \sigma_v)$.

Mit $A = 2$, $B = -2$, $D = 1$ und $E = 3$ erhält man:

$$\rho_{xy } = \frac {\it A \cdot D + B \cdot E}{\sqrt{(\it A^{\rm 2}+\it B^{\rm 2})(\it D^{\rm 2}+\it E^{\rm 2})}} =\frac {2 \cdot 1 -2 \cdot 3}{\sqrt{(4 +4)(1+9)}} = \frac {-4}{\sqrt{80}} = \frac {-1}{\sqrt{5}}\hspace{0.15cm}\underline{ = -0.447}. $$

(4)  Die Korrelationsgerade lautet allgemein:

$$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x-m_x)+m_y.$$

Aus den linearen Mittelwerten $m_u = m_v = 0.5$ und den in der Aufgabenstellung angegebenen Gleichungen erhält man $m_x = 1$ und $m_y = 2$.

Die Varianzen von $u$ und $v$ betragen jeweils $\sigma_u^2 = \sigma_v^2 =1/12$. Daraus folgt:

$$\sigma_x^2 = 4 \cdot \sigma_u^2 + 4 \cdot \sigma_v^2 = 2/3,$$

$$\sigma_y^2 = \sigma_u^2 + 9\cdot \sigma_v^2 = 5/6.$$

Setzt man diese Werte in die Gleichung der Korrelationsgeraden ein, so ergibt sich:

$$y=K(x)=\frac{\sqrt{5/6}}{\sqrt{2/3}}\cdot (\frac{-1}{\sqrt{5}})\cdot(x-1)+2= - x/{2} + 2.5.$$

Daraus folgt der Wert $y_0\hspace{0.15cm}\underline{ = 2.5}$

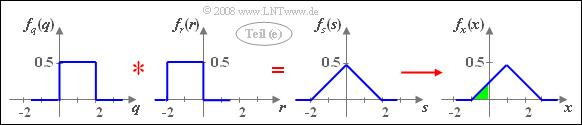
(5)  Mit den Hilfsgrößen $q= 2u$, $r= -2v$ und $s= x-1$ gilt der Zusammenhang: $s= q+r$. Da $u$ und $v$ jeweils zwischen $0$ und $1$ gleichverteilt sind, besitzt $q$ eine Gleichverteilung im Bereich von $0$ bis $2$ und $r$ eine Gleichverteilung zwischen $-2$ und $0$.

Da zudem $q$ und $r$ nicht statistisch voneinander abhängen, gilt für die WDF der Summe:

$$f_s(s) = f_q(q) \star f_r(r).$$

Die Addition$x = s+1$ führt zu einer Verschiebung der Dreieck–WDF um $1$ nach rechts. Für die gesuchte Wahrscheinlichkeit (im folgenden Bild grün hinterlegt) gilt deshalb: ${\rm Pr}(x < 0)\hspace{0.15cm}\underline{ = 0.125}$.

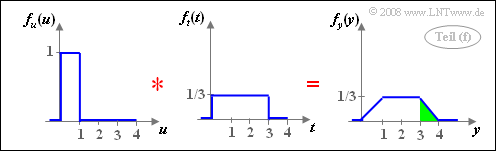
(6)  Analog zur Musterlösung für die Teilaufgabe (5) gilt mit $t = 3v$:

$$f_y(y) = f_u(u) \star f_t(t).$$

Die Faltung zwischen zwei unterschiedlich breiten Rechteckfunktionen ergibt ein Trapez. Für die gesuchte Wahrscheinlichkeit erhält man ${\rm Pr}(y>3) =1/6\hspace{0.15cm}\underline{ \approx 0.167}$. Diese Wahrscheinlichkeit ist im folgenden Bild grün hinterlegt.