Difference between revisions of "Aufgaben:Exercise 3.7Z: Which Code is Catastrophic?"
m (Guenter verschob die Seite Aufgabe 3.7Z: Welcher Code ist katastrophal nach Aufgabe 3.7Z: Welcher Code ist katastrophal?) |
|||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm}} | {{quiz-Header|Buchseite=Kanalcodierung/Codebeschreibung mit Zustands– und Trellisdiagramm}} | ||
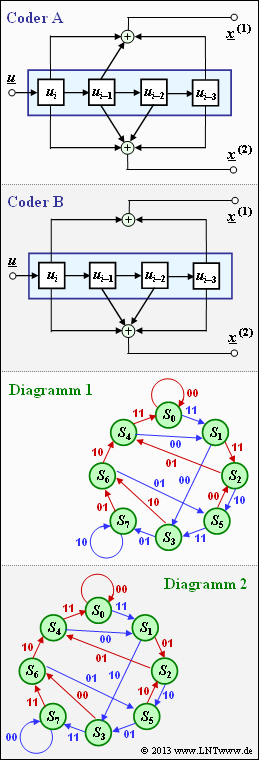
| − | [[File:P_ID2671__KC_Z_3_7.png|right|frame|Codierer | + | [[File:P_ID2671__KC_Z_3_7.png|right|frame|Codierer für $m = 3$und Zustandsübergangsdiagramm]] |
Die nebenstehende Grafik zeigt | Die nebenstehende Grafik zeigt | ||
| − | * zwei unterschiedliche | + | * zwei unterschiedliche <b>Coder A</b> und <b>Coder B</b>, jeweils mit dem Gedächtnis $m = 3$ (oben), |
| − | * zwei Zustandsübergangsdiagramme, bezeichnet mit | + | * zwei Zustandsübergangsdiagramme, bezeichnet mit <b>Diagramm 1</b> und <b>Diagramm 2</b> (unten). |
| − | In der letzten Teilaufgabe sollen Sie entscheiden, welches Diagramm zum Coder A gehört und welches zum Coder B. | + | In der letzten Teilaufgabe sollen Sie entscheiden, welches Diagramm zum '''Coder A''' gehört und welches zum '''Coder B'''. |
Zunächst werden die drei Übertragungsfunktionen | Zunächst werden die drei Übertragungsfunktionen | ||
| Line 16: | Line 16: | ||
analysiert und anschließend die Ausgangssequenzen $\underline{x}$ unter der Voraussetzung | analysiert und anschließend die Ausgangssequenzen $\underline{x}$ unter der Voraussetzung | ||
| − | :$$\underline{u}= \underline{1}= (1, 1, 1, ... \hspace{0. | + | :$$\underline{u}= \underline{1}= (1, 1, 1, \text{...} \hspace{0.05cm}) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} |
U(D)= \frac{1}{1+D}$$ | U(D)= \frac{1}{1+D}$$ | ||
berechnet. Diese Übertragungsfunktionen stehen im direkten Zusammenhang mit den skizzierten Codierern. | berechnet. Diese Übertragungsfunktionen stehen im direkten Zusammenhang mit den skizzierten Codierern. | ||
| − | Desweiteren ist noch zu klären, welcher der beiden Codes <i>katastrophal</i> ist. Von einem solchen spricht man, wenn eine endliche Anzahl von Übertragungsfehlern zu unendlich vielen Decodierfehlern führt. | + | Desweiteren ist noch zu klären, welcher der beiden Codes <i>katastrophal</i> ist. Von einem solchen spricht man dann, wenn eine endliche Anzahl von Übertragungsfehlern zu unendlich vielen Decodierfehlern führt. |
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm| Codebeschreibung mit Zustands– und Trellisdiagramm]] | + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Codebeschreibung_mit_Zustands%E2%80%93_und_Trellisdiagramm| Codebeschreibung mit Zustands– und Trellisdiagramm]]. |
| + | *Bezug genommen wird insbesondere auf die Abschnitte [[Kanalcodierung/Codebeschreibung_mit_Zustands–_und_Trellisdiagramm#Zustandsdefinition_f.C3.BCr_ein_Speicherregister|Zustandsdefinition für ein Speicherregister]] sowie [[Kanalcodierung/Codebeschreibung_mit_Zustands–_und_Trellisdiagramm#Darstellung im_Zustands.C3.BCbergangsdiagramm|Darstellung im Zustandsübergangsdiagramm]]. | ||
* Angegeben werden noch zwei Polynomprodukte in ${\rm GF}(2)$: | * Angegeben werden noch zwei Polynomprodukte in ${\rm GF}(2)$: | ||
| − | :$$(1+D) \cdot (1+D^2) | + | :$$(1+D) \cdot (1+D^2) = 1+D +D^2+D^3\hspace{0.05cm},$$ |
| − | :$$(1+D) \cdot (1+D+D^2) | + | :$$(1+D) \cdot (1+D+D^2) = 1+D^3\hspace{0.05cm}.$$ |
| Line 40: | Line 45: | ||
{Welche Ausgangssequenz $\underline{x}$ ergibt sich für $\underline{u} = \underline{1}, \ G(D) = 1 + D + D^2 + D^3$? | {Welche Ausgangssequenz $\underline{x}$ ergibt sich für $\underline{u} = \underline{1}, \ G(D) = 1 + D + D^2 + D^3$? | ||
|type="[]"} | |type="[]"} | ||
| − | - $\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, ...)$, | + | - $\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, \text{...} \hspace{0.05cm})$, |
| − | + $\underline{x} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$, | + | + $\underline{x} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, \text{...} \hspace{0.05cm})$, |
| − | - $\underline{x} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, ...)$. | + | - $\underline{x} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, \text{...} \hspace{0.05cm})$. |
+ Die Ausgangsfolge $\underline{x}$ ist zeitlich begrenzt. | + Die Ausgangsfolge $\underline{x}$ ist zeitlich begrenzt. | ||
{Welche Ausgangssequenz $\underline{x}$ ergibt sich für $\underline{u} = \underline{1}$ und $G(D) = 1 + D^3$? | {Welche Ausgangssequenz $\underline{x}$ ergibt sich für $\underline{u} = \underline{1}$ und $G(D) = 1 + D^3$? | ||
|type="[]"} | |type="[]"} | ||
| − | - $\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, ...)$, | + | - $\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, \text{...} \hspace{0.05cm})$, |
| − | - $\underline{x} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$, | + | - $\underline{x} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, \text{...} \hspace{0.05cm})$, |
| − | + $\underline{x} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, ...)$, | + | + $\underline{x} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, \text{...} \hspace{0.05cm})$, |
+ Die Ausgangsfolge $\underline{x}$ ist zeitlich begrenzt. | + Die Ausgangsfolge $\underline{x}$ ist zeitlich begrenzt. | ||
{Welche Ausgangssequenz $\underline{x}$ ergibt sich für $\underline{u} = \underline{1}$ und $G(D) = 1 + D + D^3$? | {Welche Ausgangssequenz $\underline{x}$ ergibt sich für $\underline{u} = \underline{1}$ und $G(D) = 1 + D + D^3$? | ||
|type="[]"} | |type="[]"} | ||
| − | + $\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, ...)$, | + | + $\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, \text{...} \hspace{0.05cm})$, |
| − | - $\underline{x} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$, | + | - $\underline{x} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \,\text{...} \hspace{0.05cm})$, |
| − | - $\underline{x} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, ...)$, | + | - $\underline{x} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, \text{...} \hspace{0.05cm})$, |
- Die Ausgangsfolge $\underline{x}$ ist zeitlich begrenzt. | - Die Ausgangsfolge $\underline{x}$ ist zeitlich begrenzt. | ||
| − | {Wie lautet die Codesequenz $\underline{x}$ von | + | {Wie lautet die Codesequenz $\underline{x}$ von <b>Coder A</b> für die Eins–Sequenz am Eingang? |
|type="[]"} | |type="[]"} | ||
| − | + $\underline{x} = (11, \, 00, \, 01, \, 10, \, 10, \, 10, \, ...)$, | + | + $\underline{x} = (11, \, 00, \, 01, \, 10, \, 10, \, 10, \, \text{...} \hspace{0.05cm})$, |
| − | - $\underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \, ...)$, | + | - $\underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \,\text{...} \hspace{0.05cm})$, |
| − | - $\underline{x} = (11, \, 11, \, 11, \, 11, \, 11, \, 11, \, ...)$. | + | - $\underline{x} = (11, \, 11, \, 11, \, 11, \, 11, \, 11, \,\text{...} \hspace{0.05cm})$. |
- Die Codesequenz $\underline{x}$ beinhaltet endlich viele Einsen. | - Die Codesequenz $\underline{x}$ beinhaltet endlich viele Einsen. | ||
| − | {Wie lautet die Codesequenz $\underline{x}$ von | + | {Wie lautet die Codesequenz $\underline{x}$ von <b>Coder B</b> für die Eins–Sequenz am Eingang? |
|type="[]"} | |type="[]"} | ||
| − | - $\underline{x} = (11, \, 00, \, 01, \, 10, \, 10, \, 10, \, ...)$, | + | - $\underline{x} = (11, \, 00, \, 01, \, 10, \, 10, \, 10, \, \text{...} \hspace{0.05cm})$, |
| − | + $\underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \, ... | + | + $\underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \, \text{...} \hspace{0.05cm}$, |
| − | - $\underline{x} = (11, \, 11, \, 11, \, 11, \, 11, \, 11, \, ...)$. | + | - $\underline{x} = (11, \, 11, \, 11, \, 11, \, 11, \, 11, \, \text{...} \hspace{0.05cm})$. |
+ Die Codesequenz $\underline{x}$ beinhaltet endlich viele Einsen. | + Die Codesequenz $\underline{x}$ beinhaltet endlich viele Einsen. | ||
| − | {Welche Aussagen treffen für | + | {Welche Aussagen treffen für <b>Coder B</b> zu? |
|type="[]"} | |type="[]"} | ||
- Zu Coder B gehört das Zustandsübergangsdiagramm 1. | - Zu Coder B gehört das Zustandsübergangsdiagramm 1. | ||
Revision as of 13:45, 22 January 2018
Die nebenstehende Grafik zeigt
- zwei unterschiedliche Coder A und Coder B, jeweils mit dem Gedächtnis $m = 3$ (oben),
- zwei Zustandsübergangsdiagramme, bezeichnet mit Diagramm 1 und Diagramm 2 (unten).
In der letzten Teilaufgabe sollen Sie entscheiden, welches Diagramm zum Coder A gehört und welches zum Coder B.
Zunächst werden die drei Übertragungsfunktionen
- $G(D) = 1 + D + D^2 + D^3$,
- $G(D) = 1 + D^3$, und
- $G(D) = 1 + D + D^3$
analysiert und anschließend die Ausgangssequenzen $\underline{x}$ unter der Voraussetzung
- $$\underline{u}= \underline{1}= (1, 1, 1, \text{...} \hspace{0.05cm}) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} U(D)= \frac{1}{1+D}$$
berechnet. Diese Übertragungsfunktionen stehen im direkten Zusammenhang mit den skizzierten Codierern.
Desweiteren ist noch zu klären, welcher der beiden Codes katastrophal ist. Von einem solchen spricht man dann, wenn eine endliche Anzahl von Übertragungsfehlern zu unendlich vielen Decodierfehlern führt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Codebeschreibung mit Zustands– und Trellisdiagramm.
- Bezug genommen wird insbesondere auf die Abschnitte Zustandsdefinition für ein Speicherregister sowie Darstellung im Zustandsübergangsdiagramm.
- Angegeben werden noch zwei Polynomprodukte in ${\rm GF}(2)$:
- $$(1+D) \cdot (1+D^2) = 1+D +D^2+D^3\hspace{0.05cm},$$
- $$(1+D) \cdot (1+D+D^2) = 1+D^3\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$X(D)= \frac{1+D +D^2+D^3}{1+D}= 1 +D^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x}= (1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} ... \hspace{0.1cm})\hspace{0.05cm}.$$
Zutreffend sind die Antworten 2 und 4. Berücksichtigt wurde $(1 + D) \cdot (1 + D^2) = 1 + D + D^2 + D^3$.
(2) Wegen $(1 + D) \cdot (1 + D + D^2) = 1 + D^3$ sind hier die Lösungsvorschläge 3 und 4 zutreffend:
- $$X(D)= \frac{1+D^3}{1+D}= 1 +D + D^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x}= (1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} ... \hspace{0.1cm})\hspace{0.05cm}.$$
(3) Die Polynomdivision $(1 + D + D^3)$ durch $(1 + D)$ ist im binären Galoisfeld nicht ohne Rest möglich. Man erhält $X(D) = 1 + D^3 + D^4 + D^5 + \ ... \ $ und damit die Ausgangssequenz $\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, ...)$, die sich bis ins Unendliche erstreckt. Richtig ist somit allein der Lösungsvorschlag 1.
(4) Die Übertragungsfunktionsmatrix von Coder A lautet:
- $${\boldsymbol{\rm G}}_{\rm A}(D)= \left (1 +D + D^3\hspace{0.05cm}, \hspace{0.15cm} 1+D +D^2+D^3 \right ) \hspace{0.05cm}.$$
Das jeweils erste Codebit ist deshalb durch die Sequenz entsprechend Teilaufgabe (3) gegeben und das zweite Bit durch die Sequenz entsprechend Teilaufgabe (1):
- $$\underline{x}^{(1)}\hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} ... \hspace{0.1cm})\hspace{0.05cm}, $$
- $$\underline{x}^{(2)}\hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} ... \hspace{0.1cm})$$
- $$\Rightarrow \hspace{0.3cm} \underline{x}= (11,\hspace{0.05cm} 00,\hspace{0.05cm} 01,\hspace{0.05cm} 10,\hspace{0.05cm} 10,\hspace{0.05cm} 10,\hspace{0.05cm} ... \hspace{0.1cm})\hspace{0.05cm}.$$
Dies entspricht dem Lösungsvorschlag 1.
(5) Die Übertragungsfunktion von Coder B lautet $\mathbf{G}_{\rm B} = (1 + D^3, \ 1 + D + D^2 + D^3)$. Die erste Codesequenz ergibt sich nun entsprechend Teilaufgabe (2), während $\underline{x}^{(2)}$ weiterhin der Teilaufgabe (1) entspricht. Somit erhält man hier $\underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \, ...)$ ⇒ Lösungsvorschlag 2.
Richtig ist aber auch der Lösungsvorschlag 4. Unter der hier getroffenen Annahme, dass die Einsfolge gesendet wurde $(\underline{u} = \underline{1})$, beinhaltet die Codesequenz $\underline{x}$ nur fünf Einsen. In der nächsten Teilaufgabe wird dieser Sachverhalt nochmals aufgegriffen.
(6) Wie aus dem Diagramm 1 hervorgeht, führt hier die Informationssequenz $\underline{u} = \underline{1} = (1, \, 1, \, 1, \, 1, \, 1, \, 1, \, ...)$ zur Codesequenz $\underline{x} = (11, \, 00, \, 01, \, 10, \, 10, \, 10, \, ...)$. Dies bedeutet:
- Zum Coder A gehört das Zustandsübergangsdiagramm 1.
- Zum Coder B gehört das Zustandsübergangsdiagramm 2.
Für den Coder B gelten dabei folgende Aussagen:
- $\underline{u} = \underline{0} = (0, \, 0, \, 0, \, 0, \, 0, \, 0, \, ...) \hspace{0.35cm} \Rightarrow \hspace{0.35cm} \underline{x} = (00, \, 00, \, 00, \, 00, \, 00, \, 00, \, ...)$,
- $\underline{u} = \underline{1} = (1, \, 1, \, 1, \, 1, \, 1, \, 1, \, ...) \hspace{0.35cm} \Rightarrow \hspace{0.35cm} \underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \, ...)$.
Das bedeutet: Mit nur fünf Bitfehlern an den Positionen 1, 2, 3, 5, 6 wird die Nullfolge als Einsfolge decodiert und umgekehrt. Einen solchen Code nennt man katastrophal ⇒ Lösungsvorschläge 2 und 3.