Difference between revisions of "Theory of Stochastic Signals/Probability Density Function"
| Line 8: | Line 8: | ||
== # ÜBERBLICK ZUM DRITTEN HAUPTKAPITEL # == | == # ÜBERBLICK ZUM DRITTEN HAUPTKAPITEL # == | ||
<br> | <br> | ||
| − | Wir betrachten im Folgenden kontinuierliche Zufallsgrößen, also Zufallsgrößen, die zumindest in gewissen Wertebereichen unendlich viele verschiedene Werte annehmen können. Deren Anwendungen sind in der Informations | + | Wir betrachten im Folgenden kontinuierliche Zufallsgrößen, also Zufallsgrößen, die zumindest in gewissen Wertebereichen unendlich viele verschiedene Werte annehmen können. Deren Anwendungen sind in der Informations– und Kommunikationstechnik von vielfältiger Art. Sie werden unter Anderem für die Simulation von Rauschsignalen und zur Beschreibung von Fadingeinflüssen herangezogen. |
| − | Wir beschränken uns zunächst auf die statistische Beschreibung der Amplitudenverteilung. Innere statistische Bindungen der zugrundeliegenden Prozesse werden erst in den nachfolgenden | + | Wir beschränken uns zunächst auf die statistische Beschreibung der Amplitudenverteilung. Innere statistische Bindungen der zugrundeliegenden Prozesse werden erst in den nachfolgenden Hauptkapiteln 4 und 5 betrachtet. |
Im Einzelnen werden behandelt: | Im Einzelnen werden behandelt: | ||
| Line 16: | Line 16: | ||
*der Zusammenhang zwischen Wahrscheinlichkeitsdichtefunktion und Verteilungsfunktion, | *der Zusammenhang zwischen Wahrscheinlichkeitsdichtefunktion und Verteilungsfunktion, | ||
*die Berechnung der Erwartungswerte und Momente, | *die Berechnung der Erwartungswerte und Momente, | ||
| − | *einige Sonderfälle wie Gleich–, Gauß–, Rice–, Rayleigh–, Cauchy– und Exponential | + | *einige Sonderfälle wie Gleich–, Gauß–, Rice–, Rayleigh–, Cauchy– und Exponential–Verteilung, |
*die Generierung kontinuierlicher Zufallsgrößen an einem Rechner. | *die Generierung kontinuierlicher Zufallsgrößen an einem Rechner. | ||
| Line 29: | Line 29: | ||
*dem Lehrsoftwarepaket [http://en.lntwww.de/downloads/Sonstiges/Programme/LNTsim.zip LNTsim] ⇒ Link verweist auf die ZIP-Version des Programms, | *dem Lehrsoftwarepaket [http://en.lntwww.de/downloads/Sonstiges/Programme/LNTsim.zip LNTsim] ⇒ Link verweist auf die ZIP-Version des Programms, | ||
| − | *der [http://en.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_A.pdf Praktikumsanleitung - Teil A] ⇒ Link verweist auf die PDF-Version mit Kapitel 4: Seite 47-80, | + | *der [http://en.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_A.pdf Praktikumsanleitung - Teil A] ⇒ Link verweist auf die PDF-Version mit Kapitel 4: Seite 47-80, |
| − | *der [http://en.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_B.pdf Praktikumsanleitung - Teil B] ⇒ Link verweist auf die PDF-Version mit Kapitel 13: Seite 295-314. | + | *der [http://en.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_B.pdf Praktikumsanleitung - Teil B] ⇒ Link verweist auf die PDF-Version mit Kapitel 13: Seite 295-314. |
| Line 37: | Line 37: | ||
==Eigenschaften kontinuierlicher Zufallsgrößen== | ==Eigenschaften kontinuierlicher Zufallsgrößen== | ||
<br> | <br> | ||
| − | Im zweiten Hauptkapitel wurde gezeigt, dass die Amplitudenverteilung einer (wert | + | Im zweiten Hauptkapitel wurde gezeigt, dass die Amplitudenverteilung einer (wert–)diskreten Zufallsgröße vollständig durch ihre $M$ Auftrittswahrscheinlichkeiten bestimmt ist, wobei die Stufenzahl $M$ meist einen endlichen Wert besitzt. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Unter einer '''(wert–)kontinuierlichen Zufallsgrößen''' versteht man eine Zufallsgröße, deren mögliche Zahlenwerte nicht abzählbar sind ⇒ $M \to \infty$.}} |
| − | |||
| − | + | Fürt das Folgende soll gelten: | |
*Wir kennzeichnen im Weiteren wertkontinuierliche Zufallsgrößen (meist) mit $x$ im Gegensatz zu den wertdiskreten Zufallsgrößen, die wie bisher mit $z$ bezeichnet werden. | *Wir kennzeichnen im Weiteren wertkontinuierliche Zufallsgrößen (meist) mit $x$ im Gegensatz zu den wertdiskreten Zufallsgrößen, die wie bisher mit $z$ bezeichnet werden. | ||
*Über eine eventuelle Zeitdiskretisierung wird hier keine Aussage getroffen, das heißt, wertkontinuierliche Zufallsgrößen können durchaus zeitdiskret sein. | *Über eine eventuelle Zeitdiskretisierung wird hier keine Aussage getroffen, das heißt, wertkontinuierliche Zufallsgrößen können durchaus zeitdiskret sein. | ||
| − | * | + | *Wir setzen hier voraus, dass zwischen den einzelnen Abtastwerten $x_ν$ keine statistischen Bindungen bestehen, oder lassen diese zumindest außer Betracht. |
| + | [[File: P_ID41__Sto_T_3_1_S1_neu.png |right|frame| Signal und WDF eines Gaußschen Rauschsignals]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 1:}$ | + | $\text{Beispiel 1:}$ Die Grafik zeigt einen Ausschnitt eines stochastischen Rauschsignals $x(t)$, dessen Momentanwert als eine kontinuierliche Zufallsgröße $x$ aufgefasst werden kann. |
| − | |||
| − | |||
| − | |||
*Aus der rechts dargestellten ''Wahrscheinlichkeitsdichtefunktion'' (WDF) erkennt man, dass bei diesem Beispielsignal Momentanwerte um den Mittelwert $m_1$ am häufigsten auftreten. | *Aus der rechts dargestellten ''Wahrscheinlichkeitsdichtefunktion'' (WDF) erkennt man, dass bei diesem Beispielsignal Momentanwerte um den Mittelwert $m_1$ am häufigsten auftreten. | ||
| Line 64: | Line 61: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Der Wert der '''Wahrscheinlichkeitsdichtefunktion''' $f_{x}(x)$ an der Stelle $x_\mu$ ist gleich der Wahrscheinlichkeit, dass der Momentanwert der Zufallsgröße $x$ in einem (unendlich kleinen) Intervall der Breite $Δx$ um $x_\mu$ liegt, dividiert durch $Δx$: |
| − | Der Wert der '''Wahrscheinlichkeitsdichtefunktion''' $f_{x}(x)$ an der Stelle $x_\mu$ ist gleich der Wahrscheinlichkeit, dass der Momentanwert der Zufallsgröße $x$ in einem (unendlich kleinen) Intervall der Breite $Δx$ um $x_\mu$ liegt, dividiert durch $Δx$: | ||
:$$f_x(x=x_\mu) = \lim_{\rm \Delta \it x \hspace{0.05cm}\to \hspace{0.05cm}\rm 0}\frac{\rm Pr \{\it x_\mu-\rm \Delta \it x/\rm 2 \le \it x \le x_\mu \rm +\rm \Delta \it x/\rm 2\} }{\rm \Delta \it x}.$$ | :$$f_x(x=x_\mu) = \lim_{\rm \Delta \it x \hspace{0.05cm}\to \hspace{0.05cm}\rm 0}\frac{\rm Pr \{\it x_\mu-\rm \Delta \it x/\rm 2 \le \it x \le x_\mu \rm +\rm \Delta \it x/\rm 2\} }{\rm \Delta \it x}.$$ | ||
| Line 72: | Line 68: | ||
Diese äußerst wichtige Beschreibungsgröße weist folgende Eigenschaften auf: | Diese äußerst wichtige Beschreibungsgröße weist folgende Eigenschaften auf: | ||
| − | *Obwohl aus dem Zeitverlauf im [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion#Eigenschaften_kontinuierlicher_Zufallsgr.C3.B6.C3.9Fen|Beispiel 1]] zu ersehen ist, dass die häufigsten Signalanteile bei $x = m_1$ liegen und die WDF hier ihren größten Wert besitzt, ist die Wahrscheinlichkeit ${\rm Pr}(x = m_1$), dass der Momentanwert exakt gleich dem Mittelwert $m_1$ ist, identisch Null. | + | *Obwohl aus dem Zeitverlauf im [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion#Eigenschaften_kontinuierlicher_Zufallsgr.C3.B6.C3.9Fen|$\text{Beispiel 1}$]] zu ersehen ist, dass die häufigsten Signalanteile bei $x = m_1$ liegen und die WDF hier ihren größten Wert besitzt, ist die Wahrscheinlichkeit ${\rm Pr}(x = m_1$), dass der Momentanwert exakt gleich dem Mittelwert $m_1$ ist, identisch Null. |
| − | *Für die Wahrscheinlichkeit, dass die Zufallsgröße im Bereich zwischen $x_{\rm u}$ und $x_{\rm o}$ liegt, gilt: | + | *Für die Wahrscheinlichkeit, dass die Zufallsgröße im Bereich zwischen $x_{\rm u}$ und $x_{\rm o} > x_{\rm u}$ liegt, gilt: |
:$${\rm Pr}(x_{\rm u} \le x \le x_{\rm o}) = \int_{x_{\rm u}}^{x_{\rm o}} f_{x}(x) \,{\rm d}x.$$ | :$${\rm Pr}(x_{\rm u} \le x \le x_{\rm o}) = \int_{x_{\rm u}}^{x_{\rm o}} f_{x}(x) \,{\rm d}x.$$ | ||
*Als wichtige Normierungseigenschaft ergibt sich daraus für die Fläche unter der WDF mit den Grenzübergängen $x_{\rm u} → \hspace{0.05cm} – \hspace{0.05cm} ∞$ und $x_{\rm o} → +∞:$ | *Als wichtige Normierungseigenschaft ergibt sich daraus für die Fläche unter der WDF mit den Grenzübergängen $x_{\rm u} → \hspace{0.05cm} – \hspace{0.05cm} ∞$ und $x_{\rm o} → +∞:$ | ||
| Line 80: | Line 76: | ||
| − | ''Hinweis zur Nomenklatur:'' | + | ''Hinweis zur Nomenklatur:'' In der Fachliteratur wird oft zwischen der Zufallsgröße $X$ und deren Realisierungen $x ∈ X$ unterschieden. Samit würde die obige Definitionsgleichung lauten: |
| − | In der Fachliteratur wird oft zwischen der Zufallsgröße $X$ und deren Realisierungen $x ∈ X$ unterschieden. Samit | ||
:$$f_{X}(X=x) = \lim_{{\rm \Delta} x \hspace{0.05cm}\to \hspace{0.05cm} 0}\frac{{\rm Pr} \{ x-{\rm \Delta} x/2 \le X \le x +{\rm \Delta} x/ 2\}}{{\rm \Delta} x}.$$ | :$$f_{X}(X=x) = \lim_{{\rm \Delta} x \hspace{0.05cm}\to \hspace{0.05cm} 0}\frac{{\rm Pr} \{ x-{\rm \Delta} x/2 \le X \le x +{\rm \Delta} x/ 2\}}{{\rm \Delta} x}.$$ | ||
| − | Wir haben in unserem Lerntutorial auf diese genauere Nomenklatur weitgehend verzichtet, um nicht für eine Größe zwei Buchstaben zu verbrauchen. | + | Wir haben in unserem Lerntutorial $\rm LNTwww$ auf diese genauere Nomenklatur weitgehend verzichtet, um nicht für eine Größe zwei Buchstaben zu verbrauchen. |
*Kleinbuchstaben (wie $x$) bezeichnen bei uns oft Signale und Großbuchstaben (wie $X$) die zugehörigen Spektren. | *Kleinbuchstaben (wie $x$) bezeichnen bei uns oft Signale und Großbuchstaben (wie $X$) die zugehörigen Spektren. | ||
*Trotzdem müssen wir heute (2017) ehrlicher Weise zugeben, dass die Entscheidung von 2001 nicht ganz glücklich war. | *Trotzdem müssen wir heute (2017) ehrlicher Weise zugeben, dass die Entscheidung von 2001 nicht ganz glücklich war. | ||
| Line 93: | Line 88: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Wendet man die Definitionsgleichung der letzten Seite auf diskrete Zufallsgrößen an, so nimmt die WDF an einigen Stellen $x_\mu$ aufgrund des nicht verschwindend kleinen Wahrscheinlichkeitswertes und des Grenzübergangs $Δx → 0$ unendlich große Werte an. Somit ergibt sich für die WDF eine Summe von [[Signaldarstellung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals#Diracfunktion_im_Frequenzbereich|Diracfunktionen]] (bzw. ''Distributionen''): |
| − | Wendet man die Definitionsgleichung der letzten Seite auf diskrete Zufallsgrößen an, so nimmt die WDF an einigen Stellen $x_\mu$ aufgrund des nicht verschwindend kleinen Wahrscheinlichkeitswertes und des Grenzübergangs $Δx → 0$ unendlich große Werte an. Somit ergibt sich für die WDF eine Summe von [[Signaldarstellung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals#Diracfunktion_im_Frequenzbereich|Diracfunktionen]] (bzw. ''Distributionen''): | ||
:$$f_{x}(x)=\sum_{\mu=1}^{M}p_\mu\cdot {\rm \delta}( x-x_\mu).$$ | :$$f_{x}(x)=\sum_{\mu=1}^{M}p_\mu\cdot {\rm \delta}( x-x_\mu).$$ | ||
| Line 108: | Line 102: | ||
[[File:P_ID40__Sto_T_3_1_S3_NEU.png|right|frame|Signal und WDF eines Digitalsignals]] | [[File:P_ID40__Sto_T_3_1_S3_NEU.png|right|frame|Signal und WDF eines Digitalsignals]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 2:}$ | + | $\text{Beispiel 2:}$ Rechts sehen Sie einen Ausschnitt eines Rechtecksignals mit drei möglichen Werten, wobei der Signalwert $0 \hspace{0.05cm} \rm V$ doppelt so häufig wie die äußeren Signalwerte ($\pm 1 \hspace{0.05cm} \rm V$) auftritt. |
| − | Rechts sehen Sie einen Ausschnitt eines Rechtecksignals mit drei möglichen Werten, wobei der Signalwert $0 \hspace{0.05cm} \rm V$ doppelt so häufig wie die äußeren Signalwerte ($\pm 1 \hspace{0.05cm} \rm V$) auftritt. | ||
Somit lautet die dazugehörige WDF (Anteile von oben nach unten): | Somit lautet die dazugehörige WDF (Anteile von oben nach unten): | ||
| Line 131: | Line 124: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 3:}$ | + | $\text{Beispiel 3:}$ Aus den eingezeichneten grünen Pfeilen in obiger Grafik erkennt man: |
| − | Aus den eingezeichneten grünen Pfeilen in obiger Grafik erkennt man: | ||
*Der Wert $x_{\rm akt} = 0.07$ führt zum Ergebnis $i_{\rm akt} = \text{(int) }((0.07 + 4.02)/0.04) = \text{(int) }102.25$. Hierbei bedeutet $\rm (int)$ eine Integerwandlung nach der Float–Division ⇒ $i_{\rm akt} = 102$. | *Der Wert $x_{\rm akt} = 0.07$ führt zum Ergebnis $i_{\rm akt} = \text{(int) }((0.07 + 4.02)/0.04) = \text{(int) }102.25$. Hierbei bedeutet $\rm (int)$ eine Integerwandlung nach der Float–Division ⇒ $i_{\rm akt} = 102$. | ||
*Das gleiche Intervall $i_{\rm akt} = 102$ ergibt sich für alle Werte im Bereich $0.06 \le x_{\rm akt} < 0.10$, zum Beispiel also auch für $x_{\rm akt} = 0.09$. }} | *Das gleiche Intervall $i_{\rm akt} = 102$ ergibt sich für alle Werte im Bereich $0.06 \le x_{\rm akt} < 0.10$, zum Beispiel also auch für $x_{\rm akt} = 0.09$. }} | ||
Revision as of 06:44, 8 August 2018
Contents
# ÜBERBLICK ZUM DRITTEN HAUPTKAPITEL #
Wir betrachten im Folgenden kontinuierliche Zufallsgrößen, also Zufallsgrößen, die zumindest in gewissen Wertebereichen unendlich viele verschiedene Werte annehmen können. Deren Anwendungen sind in der Informations– und Kommunikationstechnik von vielfältiger Art. Sie werden unter Anderem für die Simulation von Rauschsignalen und zur Beschreibung von Fadingeinflüssen herangezogen.
Wir beschränken uns zunächst auf die statistische Beschreibung der Amplitudenverteilung. Innere statistische Bindungen der zugrundeliegenden Prozesse werden erst in den nachfolgenden Hauptkapiteln 4 und 5 betrachtet.
Im Einzelnen werden behandelt:
- der Zusammenhang zwischen Wahrscheinlichkeitsdichtefunktion und Verteilungsfunktion,
- die Berechnung der Erwartungswerte und Momente,
- einige Sonderfälle wie Gleich–, Gauß–, Rice–, Rayleigh–, Cauchy– und Exponential–Verteilung,
- die Generierung kontinuierlicher Zufallsgrößen an einem Rechner.
Weitere Informationen zum Thema „Kontinuierliche Zufallsgrößen” sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Kapitel 4: Kontinuierliche Zufallsgrößen (Programm „kon”)
- Kapitel 13: Fehlerwahrscheinlichkeit (Programm „fwk”)
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms,
- der Praktikumsanleitung - Teil A ⇒ Link verweist auf die PDF-Version mit Kapitel 4: Seite 47-80,
- der Praktikumsanleitung - Teil B ⇒ Link verweist auf die PDF-Version mit Kapitel 13: Seite 295-314.
Eigenschaften kontinuierlicher Zufallsgrößen
Im zweiten Hauptkapitel wurde gezeigt, dass die Amplitudenverteilung einer (wert–)diskreten Zufallsgröße vollständig durch ihre $M$ Auftrittswahrscheinlichkeiten bestimmt ist, wobei die Stufenzahl $M$ meist einen endlichen Wert besitzt.
$\text{Definition:}$ Unter einer (wert–)kontinuierlichen Zufallsgrößen versteht man eine Zufallsgröße, deren mögliche Zahlenwerte nicht abzählbar sind ⇒ $M \to \infty$.
Fürt das Folgende soll gelten:
- Wir kennzeichnen im Weiteren wertkontinuierliche Zufallsgrößen (meist) mit $x$ im Gegensatz zu den wertdiskreten Zufallsgrößen, die wie bisher mit $z$ bezeichnet werden.
- Über eine eventuelle Zeitdiskretisierung wird hier keine Aussage getroffen, das heißt, wertkontinuierliche Zufallsgrößen können durchaus zeitdiskret sein.
- Wir setzen hier voraus, dass zwischen den einzelnen Abtastwerten $x_ν$ keine statistischen Bindungen bestehen, oder lassen diese zumindest außer Betracht.
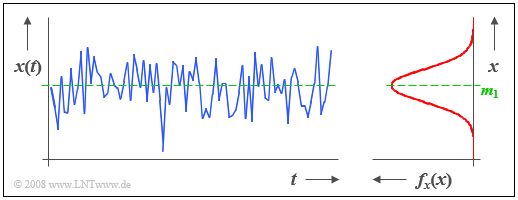
$\text{Beispiel 1:}$ Die Grafik zeigt einen Ausschnitt eines stochastischen Rauschsignals $x(t)$, dessen Momentanwert als eine kontinuierliche Zufallsgröße $x$ aufgefasst werden kann.
- Aus der rechts dargestellten Wahrscheinlichkeitsdichtefunktion (WDF) erkennt man, dass bei diesem Beispielsignal Momentanwerte um den Mittelwert $m_1$ am häufigsten auftreten.
- Da zwischen den Abtastwerten $x_ν$ keine statistischen Bindungen bestehen, bezeichnet man ein solches Signal auch als „Weißes Rauschen”.
Definition der Wahrscheinlichkeitsdichtefunktion
Bei einer kontinuierlichen Zufallsgröße $x$ sind die Wahrscheinlichkeiten, dass $x$ ganz bestimmte Werte annimmt, identisch Null. Deshalb muss zur Beschreibung einer kontinuierlichen Zufallsgröße stets auf die Wahrscheinlichkeitsdichtefunktion – abgekürzt WDF – übergegangen werden.
$\text{Definition:}$ Der Wert der Wahrscheinlichkeitsdichtefunktion $f_{x}(x)$ an der Stelle $x_\mu$ ist gleich der Wahrscheinlichkeit, dass der Momentanwert der Zufallsgröße $x$ in einem (unendlich kleinen) Intervall der Breite $Δx$ um $x_\mu$ liegt, dividiert durch $Δx$:
- $$f_x(x=x_\mu) = \lim_{\rm \Delta \it x \hspace{0.05cm}\to \hspace{0.05cm}\rm 0}\frac{\rm Pr \{\it x_\mu-\rm \Delta \it x/\rm 2 \le \it x \le x_\mu \rm +\rm \Delta \it x/\rm 2\} }{\rm \Delta \it x}.$$
Die englische Bezeichnung für die Wahrscheinlichkeitsdichtefunktion (WDF) ist Probability Density Function (PDF).
Diese äußerst wichtige Beschreibungsgröße weist folgende Eigenschaften auf:
- Obwohl aus dem Zeitverlauf im $\text{Beispiel 1}$ zu ersehen ist, dass die häufigsten Signalanteile bei $x = m_1$ liegen und die WDF hier ihren größten Wert besitzt, ist die Wahrscheinlichkeit ${\rm Pr}(x = m_1$), dass der Momentanwert exakt gleich dem Mittelwert $m_1$ ist, identisch Null.
- Für die Wahrscheinlichkeit, dass die Zufallsgröße im Bereich zwischen $x_{\rm u}$ und $x_{\rm o} > x_{\rm u}$ liegt, gilt:
- $${\rm Pr}(x_{\rm u} \le x \le x_{\rm o}) = \int_{x_{\rm u}}^{x_{\rm o}} f_{x}(x) \,{\rm d}x.$$
- Als wichtige Normierungseigenschaft ergibt sich daraus für die Fläche unter der WDF mit den Grenzübergängen $x_{\rm u} → \hspace{0.05cm} – \hspace{0.05cm} ∞$ und $x_{\rm o} → +∞:$
- $$\int_{-\infty}^{+\infty} f_{x}(x) \,{\rm d}x = \rm 1.$$
- Die entsprechende Gleichung für wertdiskrete, $M$–stufige Zufallsgrößen sagt aus, dass die Summe über alle $M$ Wahrscheinlichkeiten den Wert $1$ ergibt.
Hinweis zur Nomenklatur: In der Fachliteratur wird oft zwischen der Zufallsgröße $X$ und deren Realisierungen $x ∈ X$ unterschieden. Samit würde die obige Definitionsgleichung lauten:
- $$f_{X}(X=x) = \lim_{{\rm \Delta} x \hspace{0.05cm}\to \hspace{0.05cm} 0}\frac{{\rm Pr} \{ x-{\rm \Delta} x/2 \le X \le x +{\rm \Delta} x/ 2\}}{{\rm \Delta} x}.$$
Wir haben in unserem Lerntutorial $\rm LNTwww$ auf diese genauere Nomenklatur weitgehend verzichtet, um nicht für eine Größe zwei Buchstaben zu verbrauchen.
- Kleinbuchstaben (wie $x$) bezeichnen bei uns oft Signale und Großbuchstaben (wie $X$) die zugehörigen Spektren.
- Trotzdem müssen wir heute (2017) ehrlicher Weise zugeben, dass die Entscheidung von 2001 nicht ganz glücklich war.
WDF-Definition für diskrete Zufallsgrößen
Aus Gründen einer einheitlichen Darstellung aller Zufallsgrößen (sowohl wertdiskret als auch wertkontinuierlich) ist es zweckmäßig, die Wahrscheinlichkeitsdichtefunktion auch für diskrete Zufallsgrößen zu definieren.
$\text{Definition:}$ Wendet man die Definitionsgleichung der letzten Seite auf diskrete Zufallsgrößen an, so nimmt die WDF an einigen Stellen $x_\mu$ aufgrund des nicht verschwindend kleinen Wahrscheinlichkeitswertes und des Grenzübergangs $Δx → 0$ unendlich große Werte an. Somit ergibt sich für die WDF eine Summe von Diracfunktionen (bzw. Distributionen):
- $$f_{x}(x)=\sum_{\mu=1}^{M}p_\mu\cdot {\rm \delta}( x-x_\mu).$$
Die Gewichte dieser Diracfunktionen sind gleich den Wahrscheinlichkeiten $p_\mu = {\rm Pr}(x = x_\mu$).
Hier noch ein Hinweis, um die unterschiedlichen Beschreibungsgrößen für diskrete und kontinuierliche Zufallsgrößen einordnen zu können:
Wahrscheinlichkeit und Wahrscheinlichkeitsdichtefunktion stehen in ähnlichem Verhältnis zueinander wie im Buch Signaldarstellung
- ein diskreter Spektralanteil einer harmonischen Schwingung ⇒ Linienspektrum, und
- ein kontinuierliches Spektrum eines energiebegrenzten (impulsförmigen) Signals.
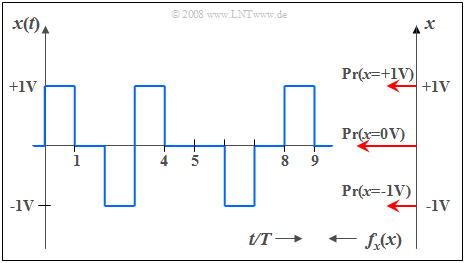
$\text{Beispiel 2:}$ Rechts sehen Sie einen Ausschnitt eines Rechtecksignals mit drei möglichen Werten, wobei der Signalwert $0 \hspace{0.05cm} \rm V$ doppelt so häufig wie die äußeren Signalwerte ($\pm 1 \hspace{0.05cm} \rm V$) auftritt.
Somit lautet die dazugehörige WDF (Anteile von oben nach unten):
- $$f_{x}(x) = 0.25 \cdot \delta(x \hspace{-0.05cm}-\hspace{-0.05cm}{\rm 1 \hspace{0.05cm} V}) \hspace{-0.05cm}+\hspace{-0.05cm} 0.5\cdot \delta(x) \hspace{-0.05cm}+\hspace{-0.05cm} 0.25\cdot \delta (x \hspace{-0.05cm} +\hspace{-0.05cm} 1\hspace{0.05cm} \rm V).$$
Zur Vertiefung der hier behandelten Thematik empfehlen wir das Lernvideo Wahrscheinlichkeit und Wahrscheinlichkeitsdichtefunktion.
Numerische Ermittlung der WDF
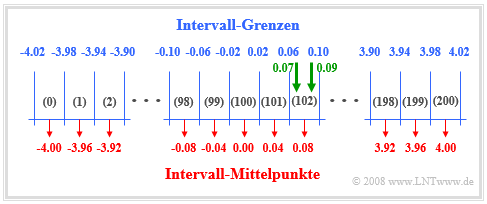
Die Grafik zeigt ein Schema zur numerischen Ermittlung der Wahrscheinlichkeitsdichtefunktion. Für die folgende Beschreibung setzen wir voraus, dass die vorliegende Zufallsgröße $x$ außerhalb des Bereichs von $x_{\rm min} = –4.02$ bis $x_{\rm max} = +4.02$ nur vernachlässigbar kleine Anteile besitzt.
Dann geht man folgendermaßen vor:
- Man teilt den Wertebereich von $x$ in $I$ Intervalle gleicher Breite $Δx$ ein und definiert ein Feld $\text{WDF}[0 : I–1]$. In obiger Skizze ist $I = 201$ und dementsprechend $Δx = 0.04$ gewählt.
- Die Zufallsgröße $x$ wird nun $N$ mal nacheinander aufgerufen und dabei jeweils geprüft, zu welchem Intervall $i_{\rm akt}$ die aktuelle Zufallsgröße $x_{\rm akt}$ gehört: $i_{\rm akt} = ({\rm int})((x + x_{\rm max})/Δx)$.
- Das entsprechende Feldelement WDF $(i_{\rm akt})$ wird dann um $1$ erhöht. Nach $N$ Durchläufen beinhaltet dann $\text{WDF}[i_{\rm akt}]$ die Anzahl der Zufallszahlen, die zum Intervall $i_{\rm akt}$ gehören.
- Die tatsächlichen WDF-Werte erhält man, wenn am Ende noch alle Feldelemente $\text{WDF}[i]$ mit $0 ≤ i < I$ durch $N · Δx$ dividiert werden.
$\text{Beispiel 3:}$ Aus den eingezeichneten grünen Pfeilen in obiger Grafik erkennt man:
- Der Wert $x_{\rm akt} = 0.07$ führt zum Ergebnis $i_{\rm akt} = \text{(int) }((0.07 + 4.02)/0.04) = \text{(int) }102.25$. Hierbei bedeutet $\rm (int)$ eine Integerwandlung nach der Float–Division ⇒ $i_{\rm akt} = 102$.
- Das gleiche Intervall $i_{\rm akt} = 102$ ergibt sich für alle Werte im Bereich $0.06 \le x_{\rm akt} < 0.10$, zum Beispiel also auch für $x_{\rm akt} = 0.09$.
Aufgaben zum Kapitel
Aufgabe 3.1: $\cos^2$ - und Dirac-WDF
Aufgabe 3.1Z: Dreieckförmige WDF