Difference between revisions of "Aufgaben:Exercise 2.4Z: Triangular Function"
From LNTwww
m (Oezdemir moved page Aufgabe 2.4Z: Triangular Function to Exercise 2.4Z: Triangular Function) |
|||
| Line 4: | Line 4: | ||
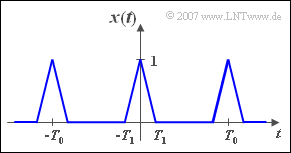
[[File:P_ID317__Sig_Z_2_4.png|right|frame|Vorgegebenes Dreiecksignal]] | [[File:P_ID317__Sig_Z_2_4.png|right|frame|Vorgegebenes Dreiecksignal]] | ||
| − | + | We consider the signal ${x(t)}$ with $T_0$ according to the adjacent sketch, where the second signal parameter $T_1 ≤ T_0/2$ is to apply. This signal is dimensionless and limited to $1$ . | |
| − | In | + | In subtask '''(3)''' the Fourier series representation $x_3(t)$ based on only $N = 3$ coefficients is used. |
| − | + | The difference between the truncated Fourier series and the actual signal is: | |
:$$\varepsilon_3(t)=x_3(t)-x(t).$$ | :$$\varepsilon_3(t)=x_3(t)-x(t).$$ | ||
| Line 17: | Line 17: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Series|Fourier Series]]. |
| − | * | + | *You can find a compact summary of the topic in the two learning videos |
::[[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|Zur Berechnung der Fourierkoeffizienten]] | ::[[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|Zur Berechnung der Fourierkoeffizienten]] | ||
:: [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]] | :: [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]] | ||
| − | * | + | *To solve the problem, you can use the following definite integral (let $n$ be an integer$)$: |
:$$\int u \cdot \cos(au)\,{\rm d}u = \frac{\cos(au)}{a^2} + \frac{u \cdot \sin(au)}{a}.$$ | :$$\int u \cdot \cos(au)\,{\rm d}u = \frac{\cos(au)}{a^2} + \frac{u \cdot \sin(au)}{a}.$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true for all permissible $T_0$ and $T_1$ ? |
|type="[]"} | |type="[]"} | ||
+ Der Gleichanteil beträgt $A_0 = T_1/T_0$. | + Der Gleichanteil beträgt $A_0 = T_1/T_0$. | ||
Revision as of 19:07, 16 January 2021
We consider the signal ${x(t)}$ with $T_0$ according to the adjacent sketch, where the second signal parameter $T_1 ≤ T_0/2$ is to apply. This signal is dimensionless and limited to $1$ .
In subtask (3) the Fourier series representation $x_3(t)$ based on only $N = 3$ coefficients is used.
The difference between the truncated Fourier series and the actual signal is:
- $$\varepsilon_3(t)=x_3(t)-x(t).$$
Hints:
- This exercise belongs to the chapter Fourier Series.
- You can find a compact summary of the topic in the two learning videos
- To solve the problem, you can use the following definite integral (let $n$ be an integer$)$:
- $$\int u \cdot \cos(au)\,{\rm d}u = \frac{\cos(au)}{a^2} + \frac{u \cdot \sin(au)}{a}.$$
Questions
Musterlösung
(1) Richtig sind die Lösungsvorschläge 1 und 2:
- Der Gleichanteil ist tatsächlich $T_1/T_0$. Da ${x(t)}$ eine gerade Funktion ist, sind alle Sinuskoeffizienten $B_n = 0$.
- Die geradzahligen Cosinuskoeffizienten $A_{2n}$ verschwinden nur dann, wenn $T_1 = T_0/2$ ist.
- In diesem Fall ist die Bedingung ${x(t)} = 2A_0 - x(t - T_0/2)$ erfüllt $($mit $A_0 = 0.5)$.
(2) Unter Ausnutzung der Symmetrieeigenschaft ${x(-t)} = {x(t)}$ erhält man:
- $$A_n=2 \cdot \frac{2}{T_0}\cdot \hspace{-0.1cm}\int_0^{T_1}(1-\frac{t}{T_1})\cos(2\pi n\frac{t}{T_0})\, {\rm d}t.$$
- Dies führt zu zwei Teilintegralen $I_1$ und $I_2$. Das erste lautet:
- $$I_1=\frac{4}{T_0} \cdot \hspace{-0.1cm} \int_0^{T_1}\cos(2\pi n\frac{t}{T_0})\,{\rm d}t=\frac{2}{\pi n}\sin(2\pi n\frac{T_1}{T_0}).$$
- Für das zweite Integral gilt mit dem Integral auf der Angabenseite:
- $$I_2=\frac{-4}{T_0\cdot T_1}\cdot \hspace{-0.1cm}\int_0^{T_1}t\cdot\cos(2\pi n\frac{t}{T_0})\,{\rm d}t=\frac{-4}{T_0\cdot T_1}\cdot \hspace{0.1cm}\left[\frac{T^2_0 \cdot \cos(2\pi nt/T_0)}{4\pi^2n^2}+\frac{T_0 \cdot t \cdot \sin(2\pi nt/T_0)}{2\pi n}\right]^{T_1}_0.$$
- Dieses letzte Integral kann wie folgt zusammengefasst werden:
- $$I_2=\frac{-\cos(2\pi nT_1/T_0)}{\pi^2 n^2T_1/T_0}+\frac{1}{\pi^2 n^2 T_1/T_0}-I_1.$$
- Daraus folgt mit $1 - \cos(2\alpha) = 2 \cdot \sin^2(\alpha)$:
- $$A_n=I_1+I_2=\frac{1-\cos(2\pi nT_1/T_0)}{\pi^2 n^2 T_1/T_0}=\frac{2\sin^2 (\pi nT_1/T_0)}{\pi^2 n^2 T_1/T_0}.$$
- Für $T_1/T_0 = 0.25$ erhält man:
- $$A_n=\frac{8\sin^2 (\pi n/4)}{\pi^2 n^2}.$$
- Insbesondere gilt:
- $$A_1=\frac{8}{\pi^2}\sin^2(\pi/4)=\frac{4}{\pi^2}\hspace{0.15cm}\underline{\approx 0.405},\hspace{0.5cm} A_2=\frac{2}{\pi^2}\sin^2(\pi/2)=\frac{2}{\pi^2}\hspace{0.15cm}\underline{\approx 0.202},\hspace{0.5cm} A_3=\frac{8}{9\pi^2}\sin^2(3\pi/4)=\frac{4}{9\pi^2}\hspace{0.15cm}\underline{\approx 0.045}.$$
(3) Es gilt:
- $$x_3(t)=\frac{1}{4}+\frac{4}{\pi^2}\left[\cos(\omega_0 t)+\frac{1}{2}\cos(2\omega_0 t)+\frac{1}{9}\cos(3\omega_0 t)\right].$$
- Zum Zeitpunkt $t = 0$ ergibt sich hieraus:
- $$x_3(t=0)=\frac{1}{4}+\frac{4}{\pi^2}\cdot \frac{29}{18}\approx 0.9 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\varepsilon_3(t=0)=x_3(t=0)-x(t=0)\hspace{0.15cm}\underline{=-0.1}.$$
- Für die Zeit $t = 0$ und bei Vielfachen der Periodendauer $T_0$ (jeweils Spitze der Dreiecksfunktionen) ist die Abweichung betragsmäßig am größten.