Difference between revisions of "Aufgaben:Exercise 4.4: Modulation in LTE"
m (Javier moved page Exercises:Exercise 4.4: Modulation in LTE to Exercise 4.4: Modulation in LTE: Text replacement - "Exercises:Exercise" to "Aufgaben:Exercise") |
m (Text replacement - "Category:Exercises for Mobile Communications" to "Category:Mobile Communications: Exercises") |
||
| (18 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Physical_Layer_for_LTE |
}} | }} | ||
| − | [[File: | + | [[File:EN_Mob_A_4_4_neu1.png|right|frame|Throughput comparison for LTE]] |
| − | + | With LTE, the scheduler selects the appropriate modulation method depending on the nature of the environment and the distance of the user from the base station. In this task, we consider various [[Modulation_Methods/Quadratur%E2%80%93Amplitudenmodulation#Allgemeine_Beschreibung_und_Signalraumzuordnung|Quadrature Amplitude Modulation]] $\rm (QAM)$ procedures, namely | |
| − | *4–QAM | + | *$\rm 4–QAM$ with $b\text{ = 2 bit/symbol}$, |
| − | * | + | *$\rm 16–QAM$ with $b\text{ = 4 bit/symbol}$, |
| − | * | + | *$\rm 64–QAM$ with $b\text{ = 6 bit/symbol}$. |
| − | + | Formally, these procedures can be described as $b^{2}–{\rm QAM}$. The signal space constellations for 16-QAM and 64-QAM are shown on the right. The bright dots indicate the 4–QAM. | |
| − | + | The lower diagram from [MG08] shows for different $b$ values the throughput depending on $10 \cdot {\rm lg \ SNR}$ <br>with $\rm SNR$ ⇒ "signal-to-noise ratio". | |
| + | You can see that for a very good channel $($very large $\rm SNR)$ the throughput is approximately proportional to $b$. | ||
| Line 21: | Line 22: | ||
| − | '' | + | |
| − | * | + | ''Notes:'' |
| − | * | + | *This task belongs to the chapter [[Mobile_Communications/Physical_Layer_for_LTE|Physical Layer for LTE]]. |
| − | * | + | *Reference is made in particular to the pages [[Mobile_Communications/Physical_Layer_for_LTE#Modulation_for_LTE|Modulation for LTE]] as well as to chapter [[Modulation_Methods#collapse4|Digital Modulation Methods]] in the book „Modulation Methods”. |
| − | * | + | * In subtask '''(1)''' the areas $\rm A$, $\rm B$ and $\rm C$ shown in the above sketch are to be assigned to the modulation methods 4-QAM, 16-QAM and 64-QAM. |
| + | *The literature reference [MG08] refers to: Myung, H.; Goodman, D.: <br> Single Carrier FDMA - A New Air Interface for Long Term Evolution. West Sussex: John Wiley & Sons, 2008. | ||
| − | === | + | ===Questionnaire=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which assignments apply in the areas $\rm A$, $\rm B$ and $\rm C$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The modulation method for area $\rm A$ is 4-QAM. |
| − | + | + | + The modulation method for area $\rm B$ is 16-QAM. |
| − | - | + | - The modulation method for area $\rm C$ is 64-QAM. |
| − | { | + | {From which signal-to-noise ratio $(\rm SNR_{1})$ is 16-QAM better than 4-QAM? |
|type="{}"} | |type="{}"} | ||
$10 \cdot \rm lg \ SNR_{1} \ = \ $ { 15 3% } $\ \rm dB$ | $10 \cdot \rm lg \ SNR_{1} \ = \ $ { 15 3% } $\ \rm dB$ | ||
| − | { | + | {From which signal-to-noise ratio $(\rm SNR_{2})$ is 64-QAM better than 16-QAM? |
|type="{}"} | |type="{}"} | ||
$10 \cdot \rm lg \ SNR_{2} \ = \ $ { 22 3% } $\ \rm dB$ | $10 \cdot \rm lg \ SNR_{2} \ = \ $ { 22 3% } $\ \rm dB$ | ||
| − | { | + | {Which modulation method would be most suitable for $10 \cdot {\rm lg \ SNR} = 5 \ \rm dB$ ? |
|type="()"} | |type="()"} | ||
| − | + BPSK ( | + | + BPSK ("Binary Phase Shift Keying"), |
| − | - QPSK ( | + | - QPSK ("Quaternary Phase Shift Keying"), |
| − | - 4–QAM. | + | - 4–QAM ("Quadrature Amplitude Modulation"). |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is only the <u>solution 2</u>: |
| − | * | + | *The area close to the transmitter $\rm A$ usually has the best reception conditions. Here the 64-QAM modulation method can be used, which allows the highest throughput under ideal conditions, but also degrades the most when the SNR decreases. |
| − | * | + | *64-QAM, on the other hand, is not suitable for the remote area $\rm C$ . Here it is better to use the lowest level modulation method "4-QAM". |
| − | [[File: | + | [[File:EN_Mob_A_4_4b_neu1.png|right|frame|Throughput of the QAM versions]] |
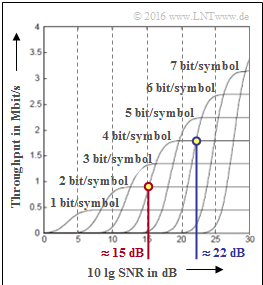
| − | '''(2)''' | + | '''(2)''' Compare here the two curves labeled $2 \ \rm bit/symbol$ and $4 \ \rm bit/symbol$. |
| − | * | + | *The point of intersection is $10 \cdot {\rm lg \ SNR_{1}}\hspace{0.15cm}\underline{ \approx 15 \ \rm dB}$. |
| − | * | + | * It follows immediately: The 16-QAM only results in a higher throughput than the 4-QAM if $10 \cdot {\rm lg \ SNR} > 15 \ \ \rm dB$. |
| − | '''(3)''' | + | '''(3)''' $10 \cdot {\rm lg \ SNR_{2}}\hspace{0.15cm}\underline{ \approx 22 \ \rm dB}$ results from the intersection of the two curves $4 \ \rm bit/symbol$ and $6 \ \rm bit/symbol$. |
| − | '''(4)''' | + | '''(4)''' From the diagram you can see that with 4-QAM $(2 \rm bit/symbol)$ the throughput is (almost) zero. |
| − | * | + | *In this comparison, the QPSK is identical to the 4-QAM and therefore unsuitable, too. |
| − | * | + | *Better would be "Binary Phase Shift Keying" $\rm (BPSK)$, which corresponds to the lowest curve $1\ \rm bit/symbol$ ⇒ <u>solution 1</u>. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 84: | Line 86: | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^4.4 Physical Layer in LTE^]] |
Latest revision as of 13:37, 23 March 2021
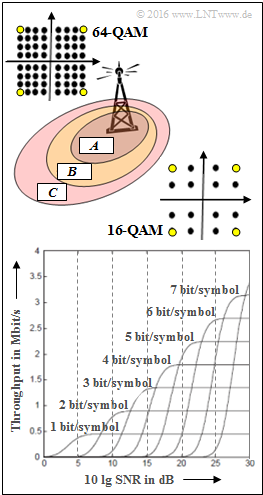
With LTE, the scheduler selects the appropriate modulation method depending on the nature of the environment and the distance of the user from the base station. In this task, we consider various Quadrature Amplitude Modulation $\rm (QAM)$ procedures, namely
- $\rm 4–QAM$ with $b\text{ = 2 bit/symbol}$,
- $\rm 16–QAM$ with $b\text{ = 4 bit/symbol}$,
- $\rm 64–QAM$ with $b\text{ = 6 bit/symbol}$.
Formally, these procedures can be described as $b^{2}–{\rm QAM}$. The signal space constellations for 16-QAM and 64-QAM are shown on the right. The bright dots indicate the 4–QAM.
The lower diagram from [MG08] shows for different $b$ values the throughput depending on $10 \cdot {\rm lg \ SNR}$
with $\rm SNR$ ⇒ "signal-to-noise ratio".
You can see that for a very good channel $($very large $\rm SNR)$ the throughput is approximately proportional to $b$.
Notes:
- This task belongs to the chapter Physical Layer for LTE.
- Reference is made in particular to the pages Modulation for LTE as well as to chapter Digital Modulation Methods in the book „Modulation Methods”.
- In subtask (1) the areas $\rm A$, $\rm B$ and $\rm C$ shown in the above sketch are to be assigned to the modulation methods 4-QAM, 16-QAM and 64-QAM.
- The literature reference [MG08] refers to: Myung, H.; Goodman, D.:
Single Carrier FDMA - A New Air Interface for Long Term Evolution. West Sussex: John Wiley & Sons, 2008.
Questionnaire
Solution
(1) Correct is only the solution 2:
- The area close to the transmitter $\rm A$ usually has the best reception conditions. Here the 64-QAM modulation method can be used, which allows the highest throughput under ideal conditions, but also degrades the most when the SNR decreases.
- 64-QAM, on the other hand, is not suitable for the remote area $\rm C$ . Here it is better to use the lowest level modulation method "4-QAM".
(2) Compare here the two curves labeled $2 \ \rm bit/symbol$ and $4 \ \rm bit/symbol$.
- The point of intersection is $10 \cdot {\rm lg \ SNR_{1}}\hspace{0.15cm}\underline{ \approx 15 \ \rm dB}$.
- It follows immediately: The 16-QAM only results in a higher throughput than the 4-QAM if $10 \cdot {\rm lg \ SNR} > 15 \ \ \rm dB$.
(3) $10 \cdot {\rm lg \ SNR_{2}}\hspace{0.15cm}\underline{ \approx 22 \ \rm dB}$ results from the intersection of the two curves $4 \ \rm bit/symbol$ and $6 \ \rm bit/symbol$.
(4) From the diagram you can see that with 4-QAM $(2 \rm bit/symbol)$ the throughput is (almost) zero.
- In this comparison, the QPSK is identical to the 4-QAM and therefore unsuitable, too.
- Better would be "Binary Phase Shift Keying" $\rm (BPSK)$, which corresponds to the lowest curve $1\ \rm bit/symbol$ ⇒ solution 1.