Difference between revisions of "Aufgaben:Exercise 2.1Z: Sum Signal"

Latest revision as of 13:33, 12 April 2021

Rectangular signal, triangular signal, sum signal

The adjacent diagram shows the periodic signals ${x(t)}$ and ${y(t)}$, from which the sum ${s(t)}$ – sketched in the lower diagram – and the difference ${d(t)}$ are formed.

Furthermore, in this task we consider the signal ${w(t)}$, which results from the sum of two periodic signals ${u(t)}$ and $v(t)$ . The base frequencies of these signals are

$f_u = 998 \,\text{Hz},$

$f_v = 1002 \,\text{Hz}.$

That is all we know about the signals ${u(t)}$ and $v(t)$.

Hints:

The exercise belongs to the chapter General description of periodic signals.
With the interactive applet Period Duration of Periodic Signals the resulting period duration of two harmonic oscillations can be determined.

Questions

$f_x\ = \ $

$\text{kHz}$

$f_y\ = \ $

$\text{kHz}$

$T_s\ = \ $

$\text{ms}$

$T_d\ = \ $

$\text{ms}$

$T_w\ = \ $

$\text{ms}$

Solution

(1) The following applies to the rectangular signal: $T_x = 1 \,\text{ms}$ ⇒

$$f_x \hspace{0.15cm}\underline{= 1 \, \text{kHz}}.$$

(2) The following applies to the triangular signal: $T_y = 2.5 \,\text{ms}$ und

$$f_y \hspace{0.15cm}\underline{= 0.4\, \text{kHz}}.$$

(3) The basic frequency $f_s$ of the sum signal $s(t)$ is the greatest common divisor $f_x = 1 \,\text{kHz}$ and $f_y = 0.4 \,\text{kHz}$.

Difference $d(t) = x(t) - y(t)$

From this follows $f_s = 200 \,\text{Hz}$ and the period duration $T_s\hspace{0.15cm}\underline{ = 5 \,\text{ms}}$.
This is also evident from the graphic on the information page.

(4) The period duration $T_d$ does not change compared to the period duration $T_s$, if the signal ${y(t)}$ is not added but subtracted:

$$T_d = T_s \hspace{0.15cm}\underline{= 5\, \text{ms}}.$$

(5) The greatest common divisor of $f_u = 998 \,\text{Hz}$ and $f_{v} = 1002 \,\text{Hz}$ is $f_w = 2 \,\text{Hz}$. The inverse of this gives the period duration $T_w \hspace{0.15cm}\underline{= 500 \,\text{ms}}$.

@@ Line 1: / Line 1: @@
-{{quiz-Header|Buchseite=Signaldarstellung/Allgemeine Beschreibung
+{{quiz-Header|Buchseite=Signal Representation/General Description
 }}
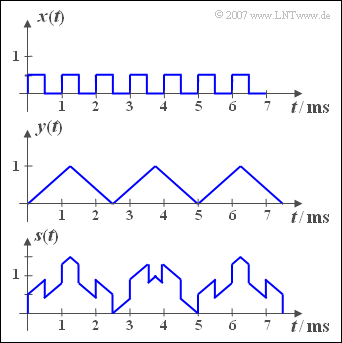
-[[File:P_ID319__Sig_Z_2_1.png|right|Summensignal ]]
+[[File:P_ID319__Sig_Z_2_1.png|right|frame|Rectangular signal, triangular signal, sum signal]]
-In der nebenstehenden Grafik sind die beiden periodischen Signale ${x(t)}$ und ${y(t)}$ dargestellt, aus denen das Summensignal ${s(t)}$ – im unteren Bild skizziert – sowie das Differenzsignal ${d(t)}$ gebildet werden.
+The adjacent diagram shows the periodic signals&nbsp; ${x(t)}$&nbsp; and&nbsp; ${y(t)}$,&nbsp; from which the sum &nbsp; ${s(t)}$&nbsp; – sketched in the lower diagram – and the difference&nbsp; ${d(t)}$&nbsp; are formed.
-Weiterhin betrachten wir in dieser Aufgabe das Signal ${w(t)}$, das sich aus der Summe der beiden periodischen Signalen ${u(t)}$ und $v(t)$ ergibt. Die Grundfrequenzen der Signale seien
+Furthermore, in this task we consider the signal&nbsp; ${w(t)}$, which results from the sum of two periodic signals&nbsp; ${u(t)}$&nbsp; and&nbsp; $v(t)$&nbsp;.&nbsp; The base frequencies of these signals are
 :* $f_u = 998 \,\text{Hz},$
-:* $f_u = 1002 \,\text{Hz}.$
+:* $f_v = 1002 \,\text{Hz}.$
-Mehr ist von diesen Signalen ${u(t)}$ und $v(t)$ nicht bekannt.
+That is all we know about the signals&nbsp; ${u(t)}$&nbsp; and&nbsp; $v(t)$.
-''Hinweise:''
-*Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Allgemeine_Beschreibung|Allgemeine Beschreibung periodischer Signale]].
-*Sollte die Eingabe des Zahlenwertes &bdquo;0&rdquo; erforderlich sein, so geben Sie bitte &bdquo;0.&rdquo; ein.
-===Fragebogen===
+''Hints:''
+*The exercise belongs to the chapter&nbsp; [[Signal_Representation/General_Description|General description of periodic signals]].
+*With the interactive applet&nbsp; [[Applets:Period_Duration_of_Periodic_Signals|Period Duration of Periodic Signals]]&nbsp; the resulting period duration of two harmonic oscillations can be determined.
+===Questions===
 <quiz display=simple>
-{Wie groß ist Periodendauer $T_x$ und Grundfrequenz $f_x$ des Signals $\text{x(t)}$?
+{What is the period duration&nbsp; $T_x$&nbsp; and the basic frequency&nbsp; $f_x$&nbsp; of the signal&nbsp; ${x(t)}$?
 |type="{}"}
-$f_x$ = { 1 3% } $\text{kHz}$
+$f_x\ = \ $  { 1 3% } &nbsp; $\text{kHz}$
-{Wie groß ist Periodendauer $T_y$ und Grundfrequenz $f_y$ des Signals $\text{y(t)}$?
+{What is the period duration&nbsp; $T_y$&nbsp; and the basic frequency&nbsp; $f_y$&nbsp; of the signal&nbsp; ${y(t)}$?
 |type="{}"}
-$f_y$ = { 0.4 3% } $\text{kHz}$
+$f_y\ = \ $ { 0.4 3% } &nbsp; $\text{kHz}$
-{Bestimmen Sie die Grundfrequenz $f_s$ sowie die Periodendauer $T_s$ des Summensignals $\text{s(t)}$ und überprüfen Sie das Ergebnis anhand der Skizze.
+{Determine the basic frequency&nbsp; $f_s$&nbsp; and the period duration&nbsp; $T_s$&nbsp; of the sum signal&nbsp; ${s(t)}$.&nbsp; <br>Verify your results with the help of the sketched signal.
 |type="{}"}
-$T_s$ = { 5 3% } $\text{ms}$
+$T_s\ = \ $ { 5 3% } &nbsp; $\text{ms}$
-{Welche Periodendauer $T_d$ weist das Differenzsignal $\text{d(t)}$ auf?
+{What is the period duration&nbsp; $T_d$&nbsp; of the difference signal&nbsp; ${d(t)}$&nbsp;?
 |type="{}"}
-$T_d$ = { 5 3% } $\text{ms}$
+$T_d\ = \ $ { 5 3% } &nbsp; $\text{ms}$
-{Welche Periodendauer $T_w$ besitzt das Signal $\text{w(t)} = \text{u(t)} + \text{$\upsilon$(t)}$?
+{What is the period duration&nbsp; $T_w$&nbsp; of the signal&nbsp; ${w(t)} = {u(t)} + v(t)$?
 |type="{}"}
-$T_w$ = { 500 3% } $\text{ms}$
+$T_w\ = \ $ { 500 3% } &nbsp; $\text{ms}$
+</quiz>
+===Solution===
+{{ML-Kopf}}
+'''(1)'''&nbsp;  The following applies to the rectangular signal:&nbsp; $T_x = 1 \,\text{ms}$  &nbsp; &rArr; &nbsp;
+:$$f_x \hspace{0.15cm}\underline{= 1 \, \text{kHz}}.$$
-</quiz>
+'''(2)'''&nbsp;   The following applies to the triangular signal:&nbsp; $T_y = 2.5 \,\text{ms}$&nbsp; und&nbsp;
+:$$f_y \hspace{0.15cm}\underline{= 0.4\,  \text{kHz}}.$$
-===Musterlösung===
+'''(3)'''&nbsp;  The basic frequency&nbsp; $f_s$&nbsp; of the sum signal&nbsp; $s(t)$&nbsp; is the greatest common divisor&nbsp; $f_x = 1 \,\text{kHz}$&nbsp; and&nbsp; $f_y = 0.4 \,\text{kHz}$.
-{{ML-Kopf}}
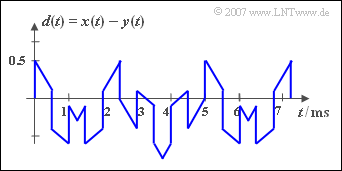
+[[File:P_ID320__Sig_Z_2_1_d_neu.png|right|frame|Difference&nbsp; $d(t) = x(t) - y(t)$]]
-'''1.'''  Es gilt $T_x = 1 \text{ms}$ und $f_x \underline{= 1 \text{kHz}}$.
+*From this follows&nbsp; $f_s = 200 \,\text{Hz}$&nbsp; and the period duration&nbsp; $T_s\hspace{0.15cm}\underline{ = 5 \,\text{ms}}$.
+* This is also evident from the graphic on the information page.
-'''2.'''  Es gilt $T_y = 2.5 \text{ms}$ und $f_y \underline{= 0.4 \text{kHz}}$.
-'''3.'''  Die Grundfrequenz $f_s$ ist der größte gemeinsame Teiler von $f_x = 1 \text{kHz}$ und $f_y = 0.4 \text{kHz}$. Daraus folgt $f_s = 200 \text{Hz}$ und die Periodendauer $T_s = 5 \text{ms}$, wie auch aus der grafischen Darstellung des Signals $\text{s(t)}$ hervorgeht.
+'''(4)'''&nbsp;  The period duration&nbsp; $T_d$&nbsp; does not change compared to the period duration&nbsp; $T_s$,&nbsp; if the signal&nbsp; ${y(t)}$&nbsp; is not added but subtracted: &nbsp; &nbsp;
+:$$T_d = T_s \hspace{0.15cm}\underline{= 5\, \text{ms}}.$$
-'''4.'''  Die Periodendauer $T_d$ ändert sich gegenüber der Periodendauer $T_s$ nicht, wenn das Signal $\text{y(t)}$ nicht addiert, sondern subtrahiert wird: $T_d = T_s = 5 \text{ms}$.
+'''(5)'''&nbsp;  The greatest common divisor of&nbsp; $f_u = 998 \,\text{Hz}$&nbsp; and&nbsp; $f_{v} = 1002 \,\text{Hz}$&nbsp; is&nbsp; $f_w = 2 \,\text{Hz}$.&nbsp; The inverse of this gives the period duration&nbsp;  $T_w \hspace{0.15cm}\underline{= 500 \,\text{ms}}$.
-[[File:P_ID320__Sig_Z_2_1_d_neu.png|center|]]
-'''5.'''  Der größte gemeinsame Teiler von $f_u = 0.998 \text{kHz}$ und $f_{\upsilon} = 1.002 \text{kHz}$ ist $f_w = 2 \text{Hz}$. Der Kehrwert hiervon ergibt die Periodendauer $T_w = 500 \text{ms}$.
 {{ML-Fuß}}
-[[Category:Aufgaben zu Signaldarstellung|^2. Periodische Signale^]]
+[[Category:Signal Representation: Exercises|^2.1 Description of Periodic Signals^]]