Aufgaben:Exercise 4.1Z: High-Pass System

• Return to book

Simplest examples for
"low-pass" and "high-pass"

The relationships shown on the page  "Properties of Bandpass Signals"  apply not only to signals and spectra, but in the same way to

• the frequency response  $H(f)$  and
• the impulse response  $h(t)$  of an LTI system.

These are also related via the  Fourier Transform.  More information can be found in the book  "Linear and Time-Invariant Systems".

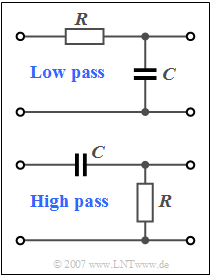
The circuit shown in the upper diagram is the simplest realisation of a low-pass  (German:  "Tiefpass"   ⇒   $\text{TP}$)  filter:

• For very high frequencies, the capacitance  $C$  acts as a short circuit, so that high-frequency components are no longer included in the output signal.
• In contrast, low-frequency signal components are only imperceptibly attenuated by the voltage divider.
• With the 3dB cut-off frequency  $f_{\rm G}$  the following applies to the frequency response:

$$H_{\rm TP}(f) = \frac{1}{1 + {\rm j} \cdot f / f_{\rm G}} = |H_{\rm TP}(f)|\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_{\rm TP}(f)} .$$

In the second part of this equation, the frequency response  $H_{\rm TP}(f)$  is split according to magnitude and phase.

The impulse response  $h_{\rm TP}(t)$  is obtained by Fourier transform of  $H_{\rm TP}(f)$, where the constant  $\tau = R \cdot C = {1}/({2\pi \cdot f_{\rm G}}) $.

For  $t < 0$  the impulse response is identically zero,  anf for positive times:

$$h_{\rm TP}(t) = \frac{1}{\tau} \cdot {\rm e}^{-t / \tau} .$$

The circuit shown below describes a high-pass filter whose frequency response  $H_{\rm HP}(f)$  and impulse response  $h_{\rm HP}(t)$  are to be determined in this task. Such a high-pass can also be interpreted as a limiting case of a band-pass.

Hints:

• This exercise belongs to the chapter  Differences and Similarities of Low-Pass and Band-Pass Signals.

Questions

1

Which of the following statements are true for the low-pass system??

	The DC transmission factor is  $H_{\rm TP}(f = 0) = 2$.
	$|H_{\rm TP}(f= f_{\rm G})|$  is smaller by  $\sqrt{2}$  than  $|H_{\rm TP}(f= 0)|$.
	The phase function is  $\varphi_{\rm TP}(f) = \arctan(f/f_{\rm G})$.

2

Justify why  $H_{\rm HP}(f) = 1 - H_{\rm TP}(f)$  must always hold.  Calculate  $H_{\rm HP}(f)$,  in particular the value at  $f = 0$.

$H_{\rm HP}(f = 0)\ = \ $

3

Which of the following statements are true?

	It holds:  $|H_{\rm HP}(f = f_{\rm G})| = 1 - |H_{\rm TP}(f = f_{\rm G})|$.
	It holds:  $|H_{\rm HP}(f = f_{\rm G})| = |H_{\rm TP}(f = f_{\rm G})|$.
	For positive frequencies it holds:   $\varphi_{\rm HP}(f) = \varphi_{\rm TP}(f) - \pi/2$.

4

Calculate the impulse response  $h_{\rm TP}(t)$.  Interpret the result.  Which of the following statements are correct?

	It holds:  $h_{\rm HP}(t) = \tau/t \cdot {\rm e}^{-t/\tau}$.
	It holds:  $h_{\rm HP}(t) = \delta (t) - 1/\tau \cdot {\rm e}^{-t/\tau}$.
	At time  $t = 0$  the impulse response is infinite.
	At time  $t = \tau$  the impulse response is equal to  ${\rm e}/\tau$.

Solution

Solution

(1)  The correct solutions are 2 and 3:

• The DC transmission factor is   $H_{\rm TP}(f = 0) = 1$.
• For the magnitude frequency response holds:

$$|H_{\rm TP}(f)| = \frac{1}{\sqrt{1 + ( f / f_{\rm G})^2}} .$$

• Thus, the value at  $f_{\rm G}$ is equal to $\sqrt{1/2}$.  The power transfer function  $|H_{\rm TP}(f)|^2$  is therefore only half as large at  $f = f_{\rm G}$  as at  $f = 0$, which is the reason for the designation "3dB cut-off frequency".
• The phase function is generally calculated according to the following equation:

$$\varphi_{\rm TP}(f) = -\arctan\frac{{\rm Im}\left[H_{\rm TP}(f)\right]}{{\rm Re}\left[H_{\rm TP}(f)\right]} .$$

• With the conjugate-complex expansion one obtains:

$$H_{\rm TP}(f) = \frac{1}{1 - ( f / f_{\rm G})^2} - \frac{{\rm j} \cdot f / f_{\rm G}}{1 - ( f / f_{\rm G})^2}.$$

• Substituting this result into the above equation gives:

$$\varphi_{\rm TP}(f) = \arctan\left(f / f_{\rm G}\right) .$$

• The progression is monotonically increasing from  $0$  $($at  $f = 0)$  via  $\pi/2$  $($at  $f = f_{\rm G})$  to  $\pi$  $($bei  $f \rightarrow \infty)$ .

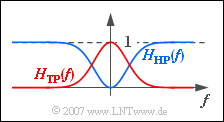
(2)  On the page  "Properties of Bandpass Signals"  it was shown that any band-pass signal can be represented as the difference of two low-pass signals.

Red:  Low-pass  $\rm (TP)$,
Blue:  High-pass  $\rm (HP)$

The same applies to frequency responses:

$$H_{\rm BP}(f) = H_1(f) - H_2(f).$$

• If we set  $H_2(f) = H_{\rm TP}(f)$  and consider  $H_1(f) = 1$  as the limiting case of a low-pass function with an infinitely large bandwidth, we get:

$$H_{\rm HP}(f) = 1 - H_{\rm TP}(f).$$

• As the graph shows, the result is now a high-pass because of   $H_1(f) = 1$.  With the given low-pass function  $H_{\rm TP}(f)$  one further obtains:

$$H_{\rm HP}(f) = 1 - \frac{1}{1 + {\rm j} \cdot f / f_{\rm G}} = \frac{{\rm j} \cdot f / f_{\rm G}}{1 + {\rm j} \cdot f / f_{\rm G}} .$$

• For  $f = 0$:    $H_{\rm HP}(f = 0) \;\underline{= 0}$ is obtained.  Note that it is the actual (complex) function  $H_{\rm TP}(f)$  and not its magnitude that is to be subtracted.  Therefore, the above sketch is to be understood only qualitatively.

One arrives at exactly the same result starting from the concrete circuit on the information page.  Corresponding to a frequency-dependent voltage divider with resistors  $R$  and  $1/(j\omega C)$  applies:

$$H_{\rm HP}(f) = \frac{R}{R + 1/({\rm j}\cdot \omega \cdot C)} = \frac{{\rm j}\cdot \omega \cdot C \cdot R}{1+{\rm j} \cdot \omega \cdot C \cdot R} = \frac{{\rm j} \cdot f / f_{\rm G}}{1 + {\rm j} \cdot f / f_{\rm G}}.$$

(3)  The correct solutions are 2 and 3:

• The magnitude function of the high-pass is:

$$|H_{\rm HP}(f)| = \frac{|f / f_{\rm G}|}{\sqrt{1 + ( f / f_{\rm G})^2}} .$$

• At the cut-off frequency  $f_{\rm G}$,  the magnitudes of the high-pass and low-pass frequency response are thus equal, namely  $0.707$ each.
• On the other hand, the first statement is obviously wrong:   According to this, the value  $|H_{HP}(f = f_{\rm G})| = 1 - 0.707 \approx 0.293$  should result.

Phase responses of
low-pass and high-pass

• The frequency response calculated under  (2)  can also be represented as follows:

$$H_{\rm HP}(f) = \frac{( f / f_{\rm G})^2 + {\rm j} \cdot f / f_{\rm G}}{{1 + ( f / f_{\rm G})^2}} .$$

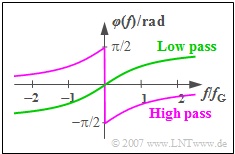
• This gives for the phase function:

$$\varphi_{\rm HP}(f) =-\arctan\frac{f / f_{\rm G}}{( f / f_{\rm G})^2}= -{\rm arcctg} ({f}/{f_{\rm G}}) $$

$$\Rightarrow \hspace{0.3cm}\varphi_{\rm HP}(f) = {\rm arctan} (\frac{f}{f_{\rm G}}) - \frac{\pi}{2}= \varphi_{\rm TP}(f)- \frac{\pi}{2}.$$

• Therefore:  At positive frequencies, the same course as with the low-pass system results, except for a shift of  $\pi /2$  downwards.  Since the phase function is odd, there is an upward shift of  $\pi /2$  at negative frequencies.

(4)  Proposed solutions 2 and 3 are correct:

• Due to the linearity of the (inverse) Fourier transform, the following applies to the time course for  $t > 0$:

$$h_{\rm HP}(t) = h_1(t) - h_2(t)= \delta(t) - \frac{1}{\tau}\cdot {\rm e}^{-t / \tau} .$$

• The Dirac function is the inverse Fourier transform of the constant frequency function „1”.
• The second component is identical to the low-pass impulse response except for the sign.
• The Dirac function causes  $h_{\rm HP}(t)$  to be infinitely large at time  $t = 0$.  In contrast, the following applies for  $t = \tau$:

$$h_{\rm HP}(t = \tau) = - \frac{1}{\tau}\cdot {\rm e}^{-1} = - {{\rm e}/ \tau}.$$

• The last statement is therefore also false due to the sign.