Difference between revisions of "Aufgaben:Exercise 4.5Z: Simple Phase Modulator"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Signaldarstellung/Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion }} right| Die Grafi…“) |
|||
| (27 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Equivalent Low-Pass Signal and its Spectral Function |
}} | }} | ||
| − | [[File:P_ID757__Sig_Z_4_5.png|right|]] | + | [[File:P_ID757__Sig_Z_4_5.png|right|frame|Model of the considered phase modulator]] |
| − | + | The diagram shows a quite simple arrangement for approximating a phase modulator. All signals are dimensionless. | |
| − | + | The sinusoidal source signal $q(t)$ of frequency $f_{\rm N} = 10 \ \text{kHz}$ is multiplied by the signal $m(t)$, which results from the cosinusoidal carrier signal $z(t)$ by phase shifting by $\phi = 90^\circ$ : | |
| − | :$$m(t) = {\cos} ( \omega_{\rm T} t + 90^\circ).$$ | + | :$$m(t) = {\cos} ( \omega_{\rm T} \cdot t + 90^\circ).$$ |
| − | |||
| − | + | Then the signal $z(t)$ with the frequency $f_{\rm T} = 1 \ \text{MHz}$ is still added directly. | |
| − | + | For abbreviation purposes, this task also uses: | |
| − | + | *the difference frequency $f_{\rm \Delta} = f_{\rm T} - f_{\rm N} = 0.99 \ \text{MHz}$, | |
| − | \ | + | *the sum frequency $f_{\rm \Sigma} = f_{\rm T} + f_{\rm N} = 1.01\ \text{MHz}$, |
| − | + | *the two circular frequencies $\omega_{\rm \Delta} = 2\pi \cdot f_{\rm \Delta}$ and $\omega_{\rm \Sigma} = 2\pi \cdot f_{\rm \Sigma}$. | |
| − | \ | ||
| − | === | + | |
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Signal_Representation/Equivalent_Low-Pass_Signal_and_its_Spectral_Function|Equivalent Low-Pass Signal and its Spectral Function]]. | ||
| + | |||
| + | *Consider the trigonomic transformations | ||
| + | :$$\sin(\alpha) \cdot \cos (\beta)= {1}/{2} \cdot \sin(\alpha - \beta) + {1}/{2} \cdot \sin(\alpha + \beta),$$ | ||
| + | :$$\sin(\alpha) \cdot \sin (\beta)= {1}/{2} \cdot \cos(\alpha - \beta) - {1}/{2} \cdot \cos(\alpha + \beta).$$ | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following equations correctly describe $s(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + $s(t) = \cos(\ | + | + $s(t) = \cos(\omega_{\rm T} \cdot t) - q(t) \cdot \sin(\omega_{\rm T} \cdot t)$. |
| − | - $s(t) = \cos(\ | + | - $s(t) = \cos(\omega_{\rm T} \cdot t) + q(t) \cdot \cos(\omega_{\rm T} \cdot t)$. |
| − | - $s(t) = \cos(\ | + | - $s(t) = \cos(\omega_{\rm T} \cdot t) + 0.5 \sin(\omega_{\rm \Delta} \cdot t) + 0.5 \sin(\omega_{\rm \Sigma} \cdot t)$. |
| − | + $s(t) = \cos(\ | + | + $s(t) = \cos(\omega_{\rm T} \cdot t) - 0.5 \cos(\omega_{\rm \Delta} \cdot t) + 0.5 \cos(\omega_{\rm \Sigma} \cdot t)$. |
| − | { | + | {Calculate the equivalent low-pass signal $s_{\rm TP}(t)$. What are the inphase and quadrature components at time $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $s_{\rm I}(t = 0)\ = \ $ { 1 3% } |
| − | $ | + | $s_{\rm Q}(t = 0)\ = \ $ { 0. } |
| + | |||
| + | {Which of the following statements are true for the "Locality Curve" $s_{\rm TP}(t)$ zu? | ||
| + | |type="()"} | ||
| + | - The locality curve is a circular arc. | ||
| + | - The locality curve is a horizontal straight line. | ||
| + | + The locality curve is a vertical straight line. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {Calculate the magnitude $a(t)$, in particular its maximum and minimum values. | ||
| − | |||
|type="{}"} | |type="{}"} | ||
| − | $a_{max}$ | + | $a_{\rm max}\ = \ $ { 1.414 3% } |
| − | $a_{min}$ | + | $a_{\rm min}\ = \ $ { 1 3% } |
| − | { | + | {What is the phase function $\phi(t)$. What is its maximum value? |
|type="{}"} | |type="{}"} | ||
| − | $\phi_{max}$ | + | $\phi_{\rm max}\ = \ $ { 45 3% } $\text{deg}$ |
| Line 57: | Line 68: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' <u>The first and last suggestions</u> are correct: |
| + | *Due to the phase shift by $\phi = 90^\circ$ the cosine function becomes the minus-sine function. | ||
| + | *With $q(t) = \sin(\omega_{\rm N} t)$ holds: | ||
:$${s(t)} = \cos({ \omega_{\rm T}\hspace{0.05cm} t }) - \sin({ | :$${s(t)} = \cos({ \omega_{\rm T}\hspace{0.05cm} t }) - \sin({ | ||
\omega_{\rm T}\hspace{0.05cm} t }) \cdot \sin({ \omega_{\rm | \omega_{\rm T}\hspace{0.05cm} t }) \cdot \sin({ \omega_{\rm | ||
| − | N}\hspace{0.05cm} t }) | + | N}\hspace{0.05cm} t }) = \cos({ \omega_{\rm T}\hspace{0.05cm} t }) - 0.5 \cdot \cos(({ |
| − | |||
\omega_{\rm T}-\omega_{\rm N})\hspace{0.05cm} t }) + 0.5 \cdot | \omega_{\rm T}-\omega_{\rm N})\hspace{0.05cm} t }) + 0.5 \cdot | ||
\cos(({ \omega_{\rm T}+\omega_{\rm N})\hspace{0.05cm} t }).$$ | \cos(({ \omega_{\rm T}+\omega_{\rm N})\hspace{0.05cm} t }).$$ | ||
| − | '''2 | + | |
| + | |||
| + | '''(2)''' The spectrum of the analytical signal is: | ||
:$$S_{\rm +}(f) = \delta (f - f_{\rm T}) - 0.5 \cdot \delta (f - | :$$S_{\rm +}(f) = \delta (f - f_{\rm T}) - 0.5 \cdot \delta (f - | ||
f_{\rm \Delta})+ 0.5 \cdot \delta (f - f_{\rm \Sigma}) .$$ | f_{\rm \Delta})+ 0.5 \cdot \delta (f - f_{\rm \Sigma}) .$$ | ||
| − | + | *By shitfing $f_{\rm T}$ one arrives at the spectrum of the equivalent low-pass signal: | |
:$$S_{\rm TP}(f) = \delta (f ) - 0.5 \cdot \delta (f + f_{\rm N})+ | :$$S_{\rm TP}(f) = \delta (f ) - 0.5 \cdot \delta (f + f_{\rm N})+ | ||
0.5 \cdot \delta (f - f_{\rm N}) .$$ | 0.5 \cdot \delta (f - f_{\rm N}) .$$ | ||
| − | + | *This leads to the time function | |
:$$s_{\rm TP}(t) = {\rm 1 } - 0.5 \cdot {\rm e}^{{-\rm | :$$s_{\rm TP}(t) = {\rm 1 } - 0.5 \cdot {\rm e}^{{-\rm | ||
j}\hspace{0.05cm} \omega_{\rm N} \hspace{0.05cm} t }+ 0.5 \cdot | j}\hspace{0.05cm} \omega_{\rm N} \hspace{0.05cm} t }+ 0.5 \cdot | ||
{\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm N} \hspace{0.05cm} t } | {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm N} \hspace{0.05cm} t } | ||
= 1 + {\rm j} \cdot \sin(\omega_{\rm N} \hspace{0.05cm} t ).$$ | = 1 + {\rm j} \cdot \sin(\omega_{\rm N} \hspace{0.05cm} t ).$$ | ||
| − | + | *At time $t = 0$ ⇒ $s_{\rm TP}(t) = 1$, is real. Thus: | |
| − | :* $ | + | :* $s_{\rm I}(t = 0) = \text{Re}[s_{\rm TP}(t = 0)]\; \underline{= 1}$, |
| − | :* $ | + | :* $s_{\rm Q}(t = 0) = \text{Ime}[s_{\rm TP}(t = 0)]\; \underline{= 0}$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | + | |
| + | [[File:P_ID762__Sig_Z_4_5_a.png|right|frame|Locality curve of a simple phase modulator]] | ||
| + | '''(3)''' The locality curve is a vertical straight line ⇒ <u>Proposition 3</u> with the following values: | ||
| + | :$$s_{\rm TP}(t = 0) = s_{\rm TP}(t = {\rm 50 \hspace{0.05cm} µ s}) | ||
| + | = \text{ ...} = 1,$$ | ||
| + | :$$s_{\rm TP}(t = {\rm 25 \hspace{0.05cm} µ s}) = s_{\rm TP}(t = | ||
| + | {\rm 125 \hspace{0.05cm} \mu s}) = \text{ ...} = 1 + {\rm j},$$ | ||
| + | :$$s_{\rm TP}(t = {\rm 75 \hspace{0.05cm} µ s}) = s_{\rm TP}(t = | ||
| + | {\rm 175 \hspace{0.05cm} \mu s}) = \text{ ...} = 1 - {\rm j}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' The magnitude (the pointer length) varies between $a_{\rm max} = \sqrt{2}\; \underline{\approx 1.414}$ and $a_{\rm min} \;\underline{= 1}$. It holds: | ||
:$$a(t) = \sqrt{1 + \sin^2(\omega_{\rm N} \hspace{0.05cm} t )}.$$ | :$$a(t) = \sqrt{1 + \sin^2(\omega_{\rm N} \hspace{0.05cm} t )}.$$ | ||
| − | + | With ideal phase modulation, on the other hand, the envelope $a(t)$ would have to be constant. | |
| + | |||
| − | '''5 | + | '''(5)''' The real part is always $1$, the imaginary part equal to $\sin(\omega_{\rm N} \cdot t) $. |
| + | *From this follows the phase function: | ||
:$$\phi(t)= {\rm arctan} \hspace{0.1cm}{\left(\sin(\omega_{\rm N} | :$$\phi(t)= {\rm arctan} \hspace{0.1cm}{\left(\sin(\omega_{\rm N} | ||
\hspace{0.05cm} t )\right)}.$$ | \hspace{0.05cm} t )\right)}.$$ | ||
| − | + | *The maximum value of the sine function is $1$. From this follows: | |
| + | :$$\phi_{\rm max} = \arctan (1) \; \underline{= \pi /4 } \; \Rightarrow \; \underline{45^\circ}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^4.3 Equivalent LP Signal and its Spectral Function^]] |
Latest revision as of 15:16, 24 May 2021
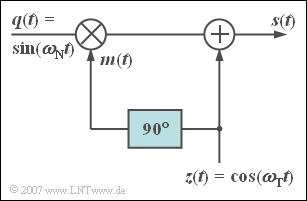
The diagram shows a quite simple arrangement for approximating a phase modulator. All signals are dimensionless.
The sinusoidal source signal $q(t)$ of frequency $f_{\rm N} = 10 \ \text{kHz}$ is multiplied by the signal $m(t)$, which results from the cosinusoidal carrier signal $z(t)$ by phase shifting by $\phi = 90^\circ$ :
- $$m(t) = {\cos} ( \omega_{\rm T} \cdot t + 90^\circ).$$
Then the signal $z(t)$ with the frequency $f_{\rm T} = 1 \ \text{MHz}$ is still added directly.
For abbreviation purposes, this task also uses:
- the difference frequency $f_{\rm \Delta} = f_{\rm T} - f_{\rm N} = 0.99 \ \text{MHz}$,
- the sum frequency $f_{\rm \Sigma} = f_{\rm T} + f_{\rm N} = 1.01\ \text{MHz}$,
- the two circular frequencies $\omega_{\rm \Delta} = 2\pi \cdot f_{\rm \Delta}$ and $\omega_{\rm \Sigma} = 2\pi \cdot f_{\rm \Sigma}$.
Hints:
- This exercise belongs to the chapter Equivalent Low-Pass Signal and its Spectral Function.
- Consider the trigonomic transformations
- $$\sin(\alpha) \cdot \cos (\beta)= {1}/{2} \cdot \sin(\alpha - \beta) + {1}/{2} \cdot \sin(\alpha + \beta),$$
- $$\sin(\alpha) \cdot \sin (\beta)= {1}/{2} \cdot \cos(\alpha - \beta) - {1}/{2} \cdot \cos(\alpha + \beta).$$
Questions
Solution
- Due to the phase shift by $\phi = 90^\circ$ the cosine function becomes the minus-sine function.
- With $q(t) = \sin(\omega_{\rm N} t)$ holds:
- $${s(t)} = \cos({ \omega_{\rm T}\hspace{0.05cm} t }) - \sin({ \omega_{\rm T}\hspace{0.05cm} t }) \cdot \sin({ \omega_{\rm N}\hspace{0.05cm} t }) = \cos({ \omega_{\rm T}\hspace{0.05cm} t }) - 0.5 \cdot \cos(({ \omega_{\rm T}-\omega_{\rm N})\hspace{0.05cm} t }) + 0.5 \cdot \cos(({ \omega_{\rm T}+\omega_{\rm N})\hspace{0.05cm} t }).$$
(2) The spectrum of the analytical signal is:
- $$S_{\rm +}(f) = \delta (f - f_{\rm T}) - 0.5 \cdot \delta (f - f_{\rm \Delta})+ 0.5 \cdot \delta (f - f_{\rm \Sigma}) .$$
- By shitfing $f_{\rm T}$ one arrives at the spectrum of the equivalent low-pass signal:
- $$S_{\rm TP}(f) = \delta (f ) - 0.5 \cdot \delta (f + f_{\rm N})+ 0.5 \cdot \delta (f - f_{\rm N}) .$$
- This leads to the time function
- $$s_{\rm TP}(t) = {\rm 1 } - 0.5 \cdot {\rm e}^{{-\rm j}\hspace{0.05cm} \omega_{\rm N} \hspace{0.05cm} t }+ 0.5 \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm N} \hspace{0.05cm} t } = 1 + {\rm j} \cdot \sin(\omega_{\rm N} \hspace{0.05cm} t ).$$
- At time $t = 0$ ⇒ $s_{\rm TP}(t) = 1$, is real. Thus:
- $s_{\rm I}(t = 0) = \text{Re}[s_{\rm TP}(t = 0)]\; \underline{= 1}$,
- $s_{\rm Q}(t = 0) = \text{Ime}[s_{\rm TP}(t = 0)]\; \underline{= 0}$.
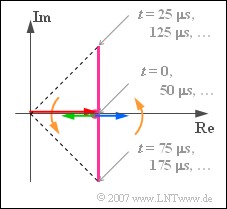
(3) The locality curve is a vertical straight line ⇒ Proposition 3 with the following values:
- $$s_{\rm TP}(t = 0) = s_{\rm TP}(t = {\rm 50 \hspace{0.05cm} µ s}) = \text{ ...} = 1,$$
- $$s_{\rm TP}(t = {\rm 25 \hspace{0.05cm} µ s}) = s_{\rm TP}(t = {\rm 125 \hspace{0.05cm} \mu s}) = \text{ ...} = 1 + {\rm j},$$
- $$s_{\rm TP}(t = {\rm 75 \hspace{0.05cm} µ s}) = s_{\rm TP}(t = {\rm 175 \hspace{0.05cm} \mu s}) = \text{ ...} = 1 - {\rm j}.$$
(4) The magnitude (the pointer length) varies between $a_{\rm max} = \sqrt{2}\; \underline{\approx 1.414}$ and $a_{\rm min} \;\underline{= 1}$. It holds:
- $$a(t) = \sqrt{1 + \sin^2(\omega_{\rm N} \hspace{0.05cm} t )}.$$
With ideal phase modulation, on the other hand, the envelope $a(t)$ would have to be constant.
(5) The real part is always $1$, the imaginary part equal to $\sin(\omega_{\rm N} \cdot t) $.
- From this follows the phase function:
- $$\phi(t)= {\rm arctan} \hspace{0.1cm}{\left(\sin(\omega_{\rm N} \hspace{0.05cm} t )\right)}.$$
- The maximum value of the sine function is $1$. From this follows:
- $$\phi_{\rm max} = \arctan (1) \; \underline{= \pi /4 } \; \Rightarrow \; \underline{45^\circ}.$$